Reihe (Mathematik)

Animation der Konvergenz der Reihe $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\cdots$ gegen 1. Mit jedem neuen Summanden wird der „Abstand“ zum Grenzwert halbiert.

Eine Reihe, selten Summenfolge oder unendliche Summe und vor allem in älteren Darstellungen auch unendliche Reihe genannt, ist ein Objekt aus dem mathematischen Teilgebiet der Analysis. Anschaulich ist eine Reihe eine Summe mit unendlich vielen Summanden, wie etwa

$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\cdots .$

Man kann Reihen als rein formale Objekte studieren, jedoch sind Mathematiker in vielen Fällen an der Frage interessiert, ob eine Reihe konvergiert, ob also die Summe endlich vieler Summanden durch Hinzunahme hinreichend vieler weiterer Summanden einem festen Wert beliebig nahe kommt. So konvergiert etwa die obige Beispielreihe gegen den Wert $1$ (siehe Bild), allerdings existieren auch divergente (also nicht konvergente) Reihen, wie zum Beispiel

$1+2+3+4+5+6+\cdots .$

Allgemein wird eine Reihe $a_0+a_1+a_2+\cdots$ mit ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ bezeichnet, und dies ist, falls existent, gleichzeitig die Bezeichnung für den Grenzwert.

Präzise wird eine Reihe als eine Folge definiert, deren Glieder die Partialsummen einer anderen Folge sind. Wenn man die Zahl 0 zur Indexmenge zählt, ist die $n$-te Partialsumme die Summe der ersten $n+1$ (von den unendlich vielen) Summanden. Falls die Folge dieser Partialsummen einen Grenzwert besitzt, so wird dieser der Wert oder die Summe der Reihe genannt.

Eine systematische Theorie der Reihen findet ihren Ursprung im 17. Jahrhundert, wo sie besonders durch Gottfried Wilhelm Leibniz und Isaac Newton vorangetrieben wurde. Dabei stand sie in enger Verbindung zu anschaulichen Problemen aus der Geometrie, wie der Integration von Kurven. Als formale Objekte wurden Reihen im 18. Jahrhundert von Mathematikern wie Leonhard Euler studiert, der ihnen drei Bände seines Gesamtwerkes, der Opera Omnia, widmete. Erst im 19. Jahrhundert stieß dieser Umgang, der Fragen nach Konvergenz oder Divergenz außen vor ließ, auf Kritik. In einer wegweisenden Schrift aus dem Jahr 1821 schuf Augustin-Louis Cauchy die Grundlagen der bis heute gebräuchlichen „quantitativen“ Theorie unendlicher Reihen und bereitete der mathematisch strengen Aufarbeitung der Analysis, etwa durch Karl Weierstraß, den Weg. Von zentraler Bedeutung in diesem Zusammenhang war das Cauchy-Kriterium für die Charakterisierung des Konvergenzbegriffs. Bis in die heutige Zeit sind Reihen, etwa im Kontext der Zahlentheorie, ein Objekt intensiver mathematischer Forschung.

Für die Untersuchung einer unendlichen Reihe sind vor allen Dingen die Fragen nach ihrer Konvergenz und, wenn diese gegeben ist, nach dem Grenzwert von Bedeutung. Für beides existieren keine brauchbaren allgemeinen Methoden. Allerdings wurden Kriterien entwickelt, die in einigen Spezialfällen Antworten liefern.

Besonders bedeutende Anwendungen haben Reihen in der Analysis (zum Beispiel über Taylorreihen zu analytischen Funktionen), den Ingenieurwissenschaften (etwa in der Elektrotechnik und Signalverarbeitung über Fourierreihen), aber auch in der Wirtschaftswissenschaft und Finanzmathematik. Einige bedeutende mathematische Konstanten, etwa die Kreiszahl $\pi$ oder die Eulersche Zahl $e$, konnten mit Hilfe von Algorithmen, die auf unendlichen Reihen fußen, auf viele Billionen Nachkommastellen angenähert werden.

Einführung

Unendliche Summierbarkeit und erste Beispiele

Die Kreiszahl $\pi$ ist irrational und hat damit unendlich viele Nachkommastellen ungleich $0$. Durch Addition der Werte $3$ und $\frac{a_n}{10^n}$ mit der $n$-ten Nachkommastelle $a_n$ lässt sie sich als Reihe darstellen.

Unter einer Reihe versteht man, veranschaulicht, eine niemals endende Summe von Zahlen. Die Dezimalschreibweise einer reellen Zahl kann zum Beispiel als Reihe aufgefasst werden, etwa

$\frac{1}{3}=0,333333\dots =0,3+0,03+0,003+0,0003+0,00003+0,000003+\cdots$

oder auch mit der Kreiszahl $\pi$:

$\pi =3,14159\dots =3+0,1+0,04+0,001+0,0005+0,00009+\cdots$.

Die durch die Punkte angedeuteten Summen enden niemals, da die Dezimalentwicklung von $\frac{1}{3}$ periodisch und die Kreiszahl irrational ist. Es gibt Reihen, denen kein Wert zugeordnet werden kann, etwa

$1+2+3+4+\cdots ,$

aber auch solche, die gegen einen Grenzwert konvergieren (wie die obigen Beispiele mit Grenzwerten $\frac{1}{3}$ bzw. $\pi$).

Darüber hinaus treten Reihen in vielen Bereichen der Mathematik auf und besitzen zahlreiche Anwendungsmöglichkeiten. Klassischerweise treten sie dann in Erscheinung, wenn mathematische Terme beliebig gut angenähert werden sollen oder die Entwicklung (theoretisch) nicht endender Prozesse analysiert wird. Auch in der Physik spielen Reihen eine wichtige Rolle. Eine einfache „Anwendung“ kann über das klassische Paradoxon von Achilles und der Schildkröte gegeben werden:

Graphische Veranschaulichung des Paradoxons (hinsichtlich des Beispiels nicht maßstabsgetreu)

Der für seine Schnelligkeit bekannte Heros Achilles liefert sich einen Wettkampf mit einer Schildkröte. Beide starten von der gleichen Position aus. Jedoch gewährt Achilles, der einhundert Mal schneller als die Schildkröte ist, dieser 100 Meter Vorsprung. Das Paradoxon besagt nun, dass Achilles die Schildkröte niemals einholen wird: Hat nämlich Achilles 100 Meter zurückgelegt, so hat sich die Schildkröte in der Zwischenzeit einen Meter von ihrer bisherigen Position weiter bewegt. Und läuft Achilles nun auch diesen weiteren Meter, so ist ihm die Schildkröte einen weiteren Zentimeter voraus. Und bewegt sich Achilles diesen Zentimeter, so hat die Schildkröte einen Zehntel Millimeter Vorsprung usw.

Das scheinbare Paradoxon entsteht dadurch, dass die Zeit nicht berücksichtigt wurde. Genau genommen ist die Aussage, dass Achilles die Schildkröte niemals aufholen wird, nicht korrekt. Die in dem Paradoxon aufgeführten Zwischenschritte, in denen die Schildkröte stets einen rasch abnehmenden Vorsprung vor Achilles hat, sind allesamt mit Zeitabschnitten verbunden, die jedoch ebenso rasant abnehmen (zum Beispiel dann, wenn Achilles nur noch einen Zentimeter läuft). Brauchte Achilles für die ersten 100 Meter noch „eine Zeiteinheit“, so wird er für einen Meter nur noch „$\frac{1}{100}$ Zeiteinheiten“ brauchen. Im nächsten Schritt braucht er für einen Zentimeter nur noch „$\frac{1}{10000}$ Zeiteinheiten“. Der Zeitpunkt, an dem Achilles und Schildkröte schließlich die gleiche Position haben werden, ist also, da deren Abstände immer weiter abnehmen, gegeben durch die unendliche Reihe

$1+\frac{1}{100}+\frac{1}{10000}+\frac{1}{1000000}+\cdots =1,0101010101\dots =\frac{100}{99}<\mathrm{\infty }.$

Obwohl also unendlich viele Terme addiert bzw. Zeitabschnitte betrachtet wurden, entsteht im Grenzwert eine endliche Zahl bzw. wird Achilles nach endlicher Zeit, nämlich nach $\frac{100}{99}$ Zeiteinheiten, die Schildkröte einholen.

Elementare Anwendungsbeispiele

Das Konzept der Reihe spielt disziplinübergreifend eine zentrale Rolle in der Mathematik. Hauptanwendungsgebiet ist zunächst die Analysis, jedoch auch alle durch diese Sparte beeinflussten Bereiche, nicht zuletzt angewandte Gebiete wie die Ingenieurwissenschaften.

Annäherung von Funktionen

Reihen entfalten ihre Nützlichkeit zum Beispiel dann, wenn es darum geht, bestimmte Funktionen annähernd auszurechnen, die für Anwendungen zwar nützlich, aber dennoch kompliziert sind. Ein besonders berühmtes und zugleich wichtiges Beispiel ist die Darstellung der natürlichen Exponentialfunktion durch ihre Taylorreihe im Punkt $x=0$:

$e^x=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\cdots +\frac{x^n}{n!}+\cdots ,$

wobei $n!$ die Fakultät von $n$ bezeichnet. Bemerkenswert ist, dass sich jeder Term auf der rechten Seite durch die vier Grundrechenarten berechnen lässt, was auf $e^x$ nicht mehr zutrifft. Die Konstruktion dieser Reihe ist dadurch motiviert, dass die (termweise) Ableitung der rechten Seite die Reihe unverändert lässt und diese in $x=0$ den Wert 1 annimmt (was beides auch auf $e^x$ zutreffen „soll“). Für kleine Werte $x$ nähert sich diese Reihe relativ schnell dem Grenzwert $e^x$ an und ist dort für eine Berechnung durchaus geeignet. Neben der (punktweisen) Berechnungsmöglichkeit liefert diese Reihendarstellung auch erste Analysemöglichkeiten: Da für $x>0$ alle Terme positiv sind, ist erkennbar, dass die Exponentialfunktion für $x\to \mathrm{\infty }$ jede Art polynomiellen Wachstums übersteigen wird, da beliebig hohe Potenzen $x^n$ in der Summation auftreten.

Animation der Approximation des Sinus durch seine Taylorreihe

Ein weiteres Beispiel sind die Winkelfunktionen, etwa der Sinus. Es gibt auch hier kein einfaches, „geschlossenes“ Verfahren, für Eingabewerte $x$ den Ausgabewert $\sin (x)$ zu berechnen, aber mittels Reihen können gute Näherungswerte relativ schnell berechnet werden, die in der Praxis ausreichen. Es gilt die Reihenentwicklung

$\sin (x)=\frac{x}{1}-\frac{x^3}{1\cdot 2\cdot 3}+\frac{x^5}{1\cdot 2\cdot 3\cdot 4\cdot 5}-\frac{x^7}{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7}+\cdots =x-\frac{x^3}{6}+\frac{x^5}{120}-\frac{x^7}{5040}+\cdots ,$

kurz:

$\sin (x)=\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k\frac{x^{2k+1}}{(2k+1)!}.$

Etwa ist $\sin (1)=0,84147098\dots$ und, wegen $1^{2k+1}=1$ für alle $k$, als Näherung bis zum $x^7$-Term

$1-\frac{1}{6}+\frac{1}{120}-\frac{1}{5040}\approx 0,8414682.$

Wahrscheinlichkeitstheorie

Münzwurf mit einer Euromünze

Bei der Untersuchung bestimmter Zufallsexperimente in der Wahrscheinlichkeitstheorie spielen Reihen eine wichtige Rolle. Ein einfaches Beispiel betrifft den „potenziell unendlichen Münzwurf“: Eine faire Münze wird dabei so oft geworfen, bis sie das erste Mal „$K$“ (= Kopf) zeigt. Mit der anderen Möglichkeit „$Z$“ (= Zahl) gibt es damit folgende Möglichkeiten, wie das Experiment endet:

$K,ZK,ZZK,ZZZK,$ usw.

Da sowohl $K$ als auch $Z$ mit gleicher Wahrscheinlichkeit $\frac{1}{2}$ auftreten, und die Würfe unabhängig ablaufen, haben die zugehörigen Wahrscheinlichkeiten die Werte $\frac{1}{2}(K),\frac{1}{4}(ZK),\frac{1}{8}(ZZK),\dots$ usw. Da aber gleichzeitig fast sicher irgendeines dieser Ereignisse eintreten muss, folgt

$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots =1,$

wobei die $1$ als die zum fast sicheren Ereignis gehörige Wahrscheinlichkeit („100 %“) zu interpretieren ist. Die besondere Bedeutung der Theorie der Reihen in der Praxis wird in diesem Zusammenhang jedoch beim Übergang zu Erwartungswerten ersichtlich. Um dies zu sehen, hilft es, das obige Experiment als ein Glücksspiel zu deuten, bei dem zum Beispiel stets die Zahl an Euro ausgezahlt wird, die angibt, wie oft „Zahl“ geworfen wurde (also zum Beispiel 3 Euro bei ZZZK) – zu Beginn aber eine Gebühr von 2 Euro verlangt wird. Es muss der Gewinn stets mit der zugehörigen Wahrscheinlichkeit gewichtet werden, und somit beträgt der zu erwartende Gewinn

$(-2)+(\frac{0}{2}+\frac{1}{4}+\frac{2}{8}+\frac{3}{16}+\cdots )=-1$

pro Runde. Die Teilnahme an diesem Glücksspiel ist demnach nicht zu empfehlen, da der Spieler pro Runde durchschnittlich 1 Euro verlieren wird. Für die Grenzwertermittlung der Reihe, die nicht ganz einfach ist, werden Methoden aus der Analysis herangezogen.

Definition und Grundlagen

Begriff

Eine Reihe wird selten Summenfolge oder unendliche Summe und vor allem in älteren Darstellungen auch unendliche Reihe genannt.

Für reelle und komplexe Folgen

Ist eine beliebige reelle (oder komplexe) Folge ${\left(a_j\right)}_{j\in {\mathbb{N}}_0}$ gegeben (${\mathbb{N}}_0$ ist die Menge der nichtnegativen ganzen Zahlen und $\in$ bezeichnet die „ist-Element-von“-Relation), kann man aus ihr eine neue Folge ${\left(s_n\right)}_{n\in {\mathbb{N}}_0}$ der Partialsummen bilden. Die $n$-te Partialsumme ist die Summe der ersten $n+1$ Glieder von ${\left(a_j\right)}_{j\in {\mathbb{N}}_0}$, ihre Definition lautet:

$s_n:=a_0+a_1+\cdots +a_n.$

Die Folge ${\left(s_n\right)}_{n\in {\mathbb{N}}_0}$ der $n$-ten Partialsummen heißt Reihe.

Zu bemerken ist, dass aus der Definition folgt, dass andersherum jede Zahlenfolge $a_0,a_1,a_2,a_3,\dots$ zu einer Reihe wird, wenn man diese als Partialsummen der Folge $a_0,(a_1-a_0),(a_2-a_1),(a_3-a_2),\dots$ auffasst. Eine Reihe ist also nichts anderes als eine Folge spezieller „Bauart“, deren Glieder rekursiv durch $s_0:=a_0$ und $s_{n+1}:=s_n+a_{n+1}$ definiert sind. Allerdings führt die einfache rekursive Struktur der Reihen zu vergleichsweise sehr handlichen Konvergenzkriterien, siehe unten.

Konvergenz und Divergenz

Obwohl Reihen auch als formale Objekte studiert werden können, also „ohne Wert“, sind in der Mathematik die Fälle von besonderem Interesse, in denen sich die Reihe langfristig einem ganz bestimmten Wert annähert. Falls die Reihe ${\sum }_{k=0}^{\mathrm{\infty }}{a}_k$, also die Folge der Partialsummen

$s_0=a_0$

$s_1=a_0+a_1$

$s_2=a_0+a_1+a_2$

$⋮$

$s_n=\sum _{k=0}^n{a}_k,\dots$ ($\sum$ ist das Summenzeichen)

konvergiert, so nennt man ihren Grenzwert

$\underset{n\to \mathrm{\infty }}{\lim }{s}_n=\underset{n\to \mathrm{\infty }}{\lim }\sum _{k=0}^n{a}_k$

den Wert der Reihe oder die Summe der Reihe. Dieser ist eindeutig bestimmt und wird meistens als ${\sum }_{k=0}^{\mathrm{\infty }}{a}_k$ notiert. Reihen, die nicht konvergieren, nennt man divergent.

Bildliche Veranschaulichung des Konvergenzprinzips. Um den Grenzwert lassen sich beliebig dünne „Schläuche“ mit Breite $\epsilon >0$ legen, und in jedem noch so dünnen Schlauch liegen fast alle Folgeglieder.

Anschaulich bedeutet Konvergenz, dass sich eine Folge auf Dauer einer reellen oder komplexen Zahl beliebig nah annähert. Da der Umgang mit „dem Unendlichen“ zunächst nicht sinnvoll ist, umgeht man diese Schwierigkeit, indem man den Konvergenzbegriff mit endlichen Mitteln erklärt. Die Reihe ${\sum }_{k=0}^{\mathrm{\infty }}{a}_k$ nennt man dann konvergent gegen den Grenzwert $S$, wenn es zu jeder noch so kleinen Zahl $\epsilon >0$ einen Index $N(\epsilon )$ gibt, sodass für alle noch größeren Indizes $N>N(\epsilon )$

$|a_0+a_1+a_2+\cdots +a_N-S|<\epsilon$

erfüllt ist. Hat eine Reihe $a_0+a_1+a_2+a_3+\cdots$ etwa den Grenzwert $1$, so besagt die Wahl $\epsilon =0,01$, dass alle bis auf endlich viele Partialsummen

$a_0+a_1+\cdots +a_N$

zwischen $0,99$ und $1,01$ liegen. Ebenso lässt sich mit $\epsilon =0,0001$ – ab einem gewissen Index liegen also alle Partialsummen zwischen $0,9999$ und $1,0001$ – usw. verfahren. In manchen Fällen ist dieses Kriterium für Konvergenz jedoch nicht brauchbar, da bereits ein Grenzwert $S$ bekannt sein muss, um es überhaupt anwenden zu können. Es ist im Allgemeinen jedoch überaus schwierig, den Grenzwert einer konvergenten Reihe anzugeben. Dies kann aber leicht umgangen werden, denn eine Reihe konvergiert genau dann, wenn es für jede Zahl $\epsilon >0$ einen Index $N(\epsilon )$ gibt, sodass für alle größeren Indizes $M\ge N>N(\epsilon )$ bereits

$|a_N+a_{N+1}+\cdots +a_{M-1}+a_M|<\epsilon$

gilt. Man bezeichnet dies als das Cauchy-Kriterium, und es kommt ohne Verwendung eines expliziten Grenzwertes aus. Allerdings eignet sich das Cauchy-Kriterium im Rahmen praktischer Konvergenztests von Reihen eher selten. Hierfür sind speziellere, aber dafür leichter handzuhabende Kriterien entwickelt worden, die jedoch nicht allgemeingültig sind (siehe unten). Häufigere Anwendung findet das Cauchy-Kriterium aber innerhalb mathematischer Beweise, etwa wenn aus der Konvergenz einer Reihe eine Schlussfolgerung gezogen werden soll. Ein erstes Beispiel ist die Aussage, dass aus der Konvergenz einer Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ bereits $a_n\to 0$ für $n\to \mathrm{\infty }$ folgt, also dass die Folge der Summanden $a_n$ eine Nullfolge bildet. In der Tat, ist $\epsilon >0$ beliebig gewählt, folgt mit dem Cauchy-Kriterium, angewandt auf den „Ein-Summand“-Spezialfall $M=N>N(\epsilon )$ schon

$|a_N|<\epsilon$ für alle $N>N(\epsilon )$.

Damit muss $a_n$ gegen 0 konvergieren. Zu beachten ist, dass die Rückrichtung dieser Aussage nicht richtig ist, da die Betrachtung einzelner Summanden $a_N$ im Allgemeinen keine wirkungsvollen Rückschlüsse auf ganze Summen $a_N+a_{N+1}+\cdots +a_{M-1}+a_M$ zulässt. Dies ist einer der Gründe schlechthin, weshalb die Theorie der unendlichen Reihen so schwierig ist.

In manchen Fällen müssen auch Reihen der Form ${\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_n=\dots +a_{-2}+a_{-1}+a_0+a_1+a_2+\dots$ untersucht werden. Diese heißen konvergent genau dann, wenn die beiden Reihen

$\sum _{n=0}^{\mathrm{\infty }}{a}_n,\sum _{n=1}^{\mathrm{\infty }}{a}_{-n}$

konvergieren.

Hinsichtlich divergenter Reihen ist zu beachten, dass das Phänomen der Divergenz keinesfalls mit der Unbeschränktheit der Partialsummen gleichzusetzen ist. So existieren divergente Reihen, deren Partialsummen beschränkt sind, zum Beispiel

$1-1+1-1+1-1+\cdots$

Das Themenfeld der Reihenkonvergenz ist bis heute ein schwieriges Gebiet, und es gibt kein allgemeingültiges und zugleich brauchbares Kriterium, um schnell zu entscheiden, ob eine vorgelegte Reihe konvergiert oder divergiert. Ein Grund hierfür ist, dass es keinen „klaren Übergang“ zwischen Konvergenz und Divergenz gibt. So existiert etwa keine „am langsamsten konvergierende Reihe“, und ebenso keine „am langsamsten divergierende Reihe“. Ist etwa ${\sum }_{n=1}^{\mathrm{\infty }}(r_{n-1}-r_n)$ mit einer Nullfolge $r_n>0$ konvergent, so auch ${\sum }_{n=1}^{\mathrm{\infty }}(\sqrt{r_{n-1}}-\sqrt{r_n})$, und letztere Reihe konvergiert langsamer als die vorherige. Darüber hinaus zeigte Alfred Pringsheim, dass die Glieder einer konvergenten Reihe keinesfalls mit einer „Mindestgeschwindigkeit“ gegen $0$ streben müssen. Es kann sogar jede konvergente Reihe für einen Beweis dieser Behauptung herangezogen werden.

Bedingte und absolute Konvergenz

Konvergenzschema einer alternierenden Reihe, also mit wechselnden Vorzeichen gekoppelt mit monoton gegen Null fallenden Summanden

Es gibt unterschiedliche Arten der Konvergenz. Dies betrifft nicht die Konvergenzdefinition, die stets dieselbe ist, sondern die „Güte“ der Konvergenz. So kann man zwei Typen konvergenter Reihen angeben: jene, die gewissermaßen „stabil“ konvergieren, und solche, bei denen größere Vorsicht zum Nachweis einer Konvergenz geboten ist, etwa bei der Umordnung von Summanden innerhalb der Reihe.

Eine Reihe ${\sum }_{k=0}^{\mathrm{\infty }}{a}_k$ heißt absolut konvergent, wenn auch die zugehörige Reihe der Absolutbeträge ${\sum }_{k=0}^{\mathrm{\infty }}|a_k|$ konvergiert. Darin ist $|\cdot |$ die Betragsfunktion.

Durch das Summieren der Beträge werden alle möglichen Vorzeichen bzw. Ausrichtungen der $a_k$ quasi „ignoriert“, was den Nachweis einer Konvergenz erschwert, da dann kein „Wegkürzen“ mehr möglich ist. Etwa ist die alternierende Reihe

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots$

konvergent, nicht aber die harmonische Reihe

$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots .$

Es ist $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots$ ein erstes Beispiel einer bedingt konvergenten Reihe, also einer, die nicht absolut konvergiert. Zudem zeigt das Beispiel der harmonischen Reihe, dass die Eigenschaft der Glieder, eine Nullfolge zu sein, nicht ausreicht, um Konvergenz zu erreichen. Es lässt sich das Nullfolgenkriterium also nicht umkehren.

Aus mathematischer Sicht ist absolute Konvergenz ein Vorteil, da diese das Rechnen mit Reihen vereinfacht. Hintergrund dessen ist, dass sich bei absolut konvergenten Reihen kanonisch die Dreiecksungleichung verwenden lässt, was in vielen Fällen verhältnismäßig einfache Schlussfolgerungen ermöglicht. Etwa ist es im Falle bedingter Konvergenz nicht ohne Weiteres erlaubt, die Reihenfolge der Summanden zu ändern, ohne dabei möglicherweise den Grenzwert zu verändern. Damit entfällt bei bedingt konvergenten Reihen das noch für endliche Summen gültige Kommutativgesetz. Im Gegensatz dazu ist es bei absolut konvergenten Reihen unerheblich, in welcher Reihenfolge summiert wird, da der Grenzwert stets derselbe bleibt. Dies kann wie folgt gesehen werden: Ist $s:={\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ absolut konvergent und $\sigma :\mathbb{N}\to \mathbb{N}$ eine Bijektion, so findet man zu $\epsilon >0$ ein $N(\epsilon )$ mit

$\sum _{n=N+1}^{\mathrm{\infty }}|a_n|<\epsilon$ für alle $N\ge N(\epsilon )$.

Ist nun $M(\epsilon )$ groß genug, beinhaltet $\{\sigma (1),\dots ,\sigma (M(\epsilon ))\}$ die Menge $\{1,\dots ,N(\epsilon )\}$. Dann gilt für alle $M\ge M(\epsilon )$ mit der Dreiecksungleichung

$|\sum _{n=1}^M{a}_{\sigma (n)}-\sum _{n=1}^{N(\epsilon )}{a}_n|\le \sum _{n=N(\epsilon )+1}^{\mathrm{\infty }}|a_n|<\epsilon .$

Mit $|s-{\sum }_{n=1}^{N(\epsilon )}{a}_n|<\epsilon$ folgt insgesamt, wieder mit der Dreiecksungleichung,

$|s-\sum _{n=1}^M{a}_{\sigma (n)}|=|s-\sum _{n=1}^{N(\epsilon )}{a}_n+\sum _{n=1}^{N(\epsilon )}{a}_n-\sum _{n=1}^M{a}_{\sigma (n)}|\le |s-\sum _{n=1}^{N(\epsilon )}{a}_n|+|\sum _{n=1}^{N(\epsilon )}{a}_n-\sum _{n=1}^M{a}_{\sigma (n)}|<2\epsilon$ für alle $M\ge M(\epsilon ).$

Zusätzlich besagt der Riemannsche Umordnungssatz, dass bei einer bedingt konvergenten Reihe mit reellen Gliedern durch Umordnungen jede reelle Zahl als Grenzwert und auch die Divergenz der neu entstehenden Reihe erzwungen werden kann.

Die absolute Konvergenz kann auch auf Multireihen ausgedehnt werden. Konvergiert ${\sum }_{m=-\mathrm{\infty }}^{\mathrm{\infty }}|a_{m,n}|$ für jedes $n$, und konvergiert ${\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}({\sum }_{m=-\mathrm{\infty }}^{\mathrm{\infty }}|a_{m,n}|)$, dann konvergieren die Reihen

• ${\sum }_{m=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_{m,n}$ für jedes $n$,
• ${\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_{m,n}$ für jedes $m$,
• ${\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}\left({\sum }_{m=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_{m,n}\right)$

und es gilt

$\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\left(\sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_{m,n}\right)=\sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}\left(\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_{m,n}\right)$.

Geschichte

Anfänge im 17. Jahrhundert

Die Kurve hat dieselbe Länge wie das entsprechende gerade Segment.

Reihen wurden in der Mathematik hauptsächlich eingeführt, um geometrische Probleme zu lösen. Ihre zunächst eher sporadische Verwendung gewann um 1650 an Bedeutung und war zum Beispiel entscheidend für die Entstehung der Infinitesimalrechnung. Besonders zu Zeiten von Isaac Newton und Gottfried Wilhelm Leibniz wurden viele Ergebnisse erzielt, und ein großer Teil des frühen Wissens um die Reihen geht auf sie zurück.

Obwohl Reihen schon früher gelegentlich vorkamen, wurden sie in der Mathematik erst ab dem 17. Jahrhundert wirklich bedeutsam. Ihre Verwendung erfolgte vor allem im Zusammenhang mit dem Problem der Quadratur und der Abmessung von Kurven durch Einteilung in lineare Segmente (siehe auch Rektifizierbarkeit). Im 17. Jahrhundert versuchten die Mathematiker, neue Methoden für die Quadratur gekrümmter Linien zu finden, die die Schwierigkeiten der sogenannten Exhaustionsmethode vermeiden.

Der Geistliche und Mathematiker Pietro Mengoli veröffentlichte 1650 in seinem Werk Novae quadraturae arithmeticae, seu de additione fractionum Resultate bezüglich unendlicher Reihen und baute seine Argumente auf zwei Axiome auf. Unter anderem fand er die Grenzwerte:

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n(n+2)}=\frac{3}{4},\sum _{n=1}^{\mathrm{\infty }}\frac{1}{(2n+1)(2n+3)(2n+5)}=\frac{1}{12}.$

Ferner fragte er nach dem Grenzwert der Reihe

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}=1+\frac{1}{4}+\frac{1}{9}+\cdots ,$

blieb bei dessen Suche aber erfolglos. Dieses Problem wurde später von Jakob Bernoulli aufgegriffen, und schließlich als Basler Problem bekannt. Erst Leonhard Euler fand den korrekten Grenzwert $\frac{{\pi }^2}{6}$ mit der Kreiszahl $\pi$ im Jahr 1735 und veröffentlichte ihn in seinem Werk De Summis Serierum Reciprocarum.

Isaac Newton im Jahr 1689

Im Jahr 1666 verfasste Newton eine Schrift De Analysi per Aequationes Numero Terminorum Infinitas, die zwar erst 1711 publiziert wurde, aber zuvor in Manuskriptform Wellen schlug. In dieser entwickelte er das heute als Newtonverfahren bekannte Prinzip, Nullstellen einer Funktion numerisch anzunähern. Er betrachtete den Spezialfall analytischer Funktionen, und es gibt nirgends einen Hinweis darauf, dass er das Verfahren auf geometrische Weise erhalten hat. Er wandte diese Technik auf die Umkehrung von Reihen an und gewann unter anderem dadurch die Reihenentwicklungen für Sinus und Kosinus. Inspiriert durch das von John Wallis verfasste Werk Arithmetica infinitorum entdeckte er zudem die allgemeine Binomialreihe, in heutiger Notation

$(1+x{)}^{\alpha }=\sum _{k=0}^{\mathrm{\infty }}(\genfrac{}{}{0ex}{}{\alpha }{k})x^k=1+\alpha x+\frac{\alpha (\alpha -1)}{2}{x}^2+\cdots (\alpha \in ℝ,|x|<1),$

die sich zur numerischen Annäherung von Wurzeln eignet. Dies geht aus einem Brief von Newton an Leibniz aus dem Jahre 1676 hervor. Newton hat für sein Theorem jedoch nie einen Beweis geliefert, denn für ihn gab es genug numerische und experimentelle Evidenz.

Fast zur gleichen Zeit, ab 1672, befasste sich Gottfried Wilhelm Leibniz mit der Theorie der unendlichen Reihen. Diese spielte eine wichtige Rolle bei seinen späteren Beiträgen zum Aufbau der Infinitesimalrechnung. Leibniz untersuchte Reihen oft mit einer geometrischen Fragestellung oder Anschauung; Beispiele hierfür sind seine Behandlung der geometrischen Reihe und der berühmten Leibniz-Reihe

$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+\cdots =\frac{\pi }{4},$

die er über die Geometrie des Kreises erklärte.

18. Jahrhundert

Brook Taylor

Im Laufe des 18. Jahrhunderts wurde die hauptsächlich von den gegenseitigen Widersachern Newton und Leibniz initiierte Theorie der unendlichen Reihen systematisch ausgebaut. Einen ersten Höhepunkt erlebte sie durch das Werk Methodus incrementorum von Brook Taylor, das 1715 veröffentlicht wurde. Darin entwickelte Taylor die heute nach ihm benannte Taylorreihe

$f(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(a)}{n!}(x-a{)}^n$

systematisch, also die Möglichkeit, eine hinreichend gutartige Funktion anhand all ihrer Ableitungen in einem Punkt in Umgebung dieses Punktes zu rekonstruieren. Dabei bezeichnet $f^{(n)}(a)$ die $n$-te Ableitung der Funktion $f$ im Punkt $a$ und $n!:=1\cdot 2\cdot 3\cdots n$ die Fakultät von $n$. Dieser Ansatz war bereits Newton bekannt gewesen, jedoch hatte er diesbezüglich nur kurze Ausführungen geliefert und es bleibt unklar, ob er die Wichtigkeit der Potenzreihen richtig einschätzte. Diese wurde in den folgenden Jahren jedoch zunehmend erfasst. Abraham de Moivre bewies einen Satz über Potenzreihen zu rekursiven Folgen und erkannte, wie andere Mathematiker dieser Zeit, dass diese eng mit sogenannten charakteristischen Polynomen der entsprechenden Rekursion zusammenhingen. Etwa gab Daniel Bernoulli 1728 mit deren Hilfe eine geschlossene Formel für die sonst nur über eine Rekursion definierte Fibonacci-Folge an.

James Stirling argumentierte in seiner 1730 publizierten Methodus differentialis, dass langsam konvergente Reihen „ebenso unnütz“ wie divergente Reihen seien, und stellte Verfahren vor, um die Konvergenz gewisser Reihen zu beschleunigen. Diese sollten auch dazu dienen, die Werte gewisser endlicher Summen schnell ausrechnen oder zumindest approximieren zu können. Unter seinen Entdeckungen fand sich auch die nach ihm benannte Stirlingformel, welche die Fakultät einer natürlichen Zahl über einen asymptotischen Reihenausdruck sehr schnell für große $n$ annähert. Die 1742 von Colin Maclaurin veröffentlichte und zeitgleich auch von Leonhard Euler entdeckte und genutzte Euler-Maclaurin-Formel, die die Arbeiten von Newton zur geometry of fluxions aufgriff, ging in eine ähnliche Richtung. Mit ihrer Hilfe konnte Maclaurin neue Beweise zu Aussagen von Newton und Stirling über Taylorreihen anfertigen und die Reihenkonvergenz durch seinen neuartigen Zugang in einigen Fällen beschleunigen.

Leonhard Euler

Besonders wichtige Beiträge zur Theorie der Reihen lieferte jedoch Leonhard Euler. Sie galten als eines seiner Lieblingsthemenfelder, und alleine drei Bände seiner Opera Omnia sind ihnen gewidmet. Zahlreiche bedeutende Entdeckungen Eulers fußen letztlich auf seiner Intuition. Darunter fallen seine Verallgemeinerung der Fakultät über die Gammafunktion, die Lösung des Basler Problems und zahlreiche weitere gefundene Grenzwerte bestimmter Reihen, wie etwa

$\frac{1}{15}+\frac{1}{63}+\frac{1}{80}+\frac{1}{255}+\frac{1}{624}+\cdots =\frac{7}{4}-\frac{{\pi }^2}{6}$ (die Nenner sind „perfekte Quadrate minus 1, die selbst auch andere Potenzen sind“, etwa $16=4^2=2^4$ usw.)

sowie seine Entdeckung der Euler-Maclaurin-Formel im Jahr 1732 (Beweis 1736). Euler zog praktischen Nutzen aus dieser Formel, um unendliche Reihen, die langsam konvergieren, schnell numerisch anzunähern. So gab er gute Näherungen für die Werte $\zeta (3)$ und $\zeta (4)$, wobei $\zeta (s)$ die Riemannsche Zeta-Funktion bezeichnet, und fand $\zeta (2)$ auf 20 Stellen genau:

$\zeta (2)=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}\approx 1,64493406684822643647.$

Erwiesenermaßen etablierte Eulers ursprüngliche Methode der Berechnung von $\zeta (m)$ für höhere Werte von $m$ die numerische Mathematik als ein neues Forschungsgebiet. Neuartig war auch sein Zugang zur Zahlentheorie über unendliche Reihen. Mit dem sog. Satz von Euler zeigte er, dass

$\sum _{p\text{Primzahl}}\frac{1}{p}=\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\frac{1}{17}+\cdots =\mathrm{\infty }$

gilt und deutete sein Resultat dahingehend, dass Primzahlen dichter in den natürlichen Zahlen liegen müssten als Quadratzahlen. Es war zudem Euler, der als erster divergente Reihen systematisch untersuchte. Dabei entging Euler jedoch keinesfalls die Problematik, welche die Zuweisung eines Summenwertes zu einer divergenten Reihe mit sich bringen konnte. So hatte schon Guido Grandi aus

„$\frac{1}{2}=1-1+1-1+\cdots$“

die Gleichheit $0=\frac{1}{2}$ abgeleitet, und damit die Möglichkeit der Erschaffung der Welt aus dem Nichts „bewiesen“. Später bemerkte man weitere Widersprüche, die durch das unbedarfte Rechnen mit divergenten Reihen entstehen können. Obwohl Euler für seinen Umgang mit divergenten Reihen kritisiert wurde, wird sein intuitiver Zugang bis heute anerkannt. So konnte er einige korrekte Resultate mit dessen Hilfe entdecken, und seine Intuition nahm Ideen aus der Theorie der Limitierungsverfahren, die den Umgang mit divergenten Reihen ab dem 19. Jahrhundert systematisch formalisierte, vorweg.

Nach 1760 entwickelte sich die Theorie der unendlichen Reihen schließlich maßgeblich in die Richtung, die Euler vorgegeben hatte. Der formale Zugang (es wurden etwa Fragen der Konvergenz oft ignoriert, und Terme wurden abstrakt umgeformt) bereitete vielen bemerkenswerten Resultaten den Boden, etwa der Lagrangeschen Inversionsformel, 1768 gezeigt von Joseph-Louis Lagrange in seiner Nouvelle méthode pour résoudre les équations littérales par le moyen des séries, und der Theorie erzeugender Funktionen von Pierre-Simon Laplace. Im Jahr 1797 konnte Lagrange schließlich die Theorie der analytischen Funktionen konstruieren mit dem Ziel, die Differentialrechnung rein durch formale Betrachtungen aufzubauen.

19. Jahrhundert

Augustin-Louis Cauchy

Zu Beginn des 19. Jahrhunderts stieß die formale Herangehensweise an die Theorie der unendlichen Reihen, also etwa jenseits von Fragen der Konvergenz, zunehmend auf Ablehnung. Ziel war es, zu einem „quantitativen Verständnis“ von Reihen zu gelangen. Die erste Arbeit in diese Richtung stammt von Carl Friedrich Gauß aus dem Jahr 1813. Zuvor hatte Joseph Fourier bereits Reihen trigonometrischer Funktionen untersucht, dabei aber einen anderen Ansatz gewählt als vorher Euler und Lagrange. Schließlich gab Augustin-Louis Cauchy die erste systematische Abhandlung eines rein quantitativen Zugangs zur Theorie der Reihen im Jahr 1821. Ein wesentlicher Grund, weshalb die formale Herangehensweise nicht mehr breite Akzeptanz fand, war, dass sie an einen Punkt gelangt war, an der die Analysis nicht weiter wachsen konnte. Cauchy erklärte dazu:

Im weiteren Verlauf verlagerte sich der Forschungsschwerpunkt entsprechend auf den „quantitativen Umgang“ mit Reihen, der sich in vielerlei Hinsicht als schwieriger und gleichzeitig fruchtbarer erwies. So kam die Frage nach Kriterien auf, wie man entscheiden könnte, ob eine unendliche Reihe überhaupt konvergiert. Beiträge in diese Richtung stammen unter anderem von Niels Henrik Abel, Augustin-Louis Cauchy, Peter Gustav Lejeune Dirichlet und Carl Friedrich Gauß. In dieser Zeit machten sich auch Cauchy und Karl Weierstraß um den Aufbau der modernen Funktionentheorie verdient. Besonders Weierstraß verwendete dafür systematisch eine moderne, bis heute gebräuchliche Theorie der Potenzreihen. In seinem 1859 verfassten Artikel Über die Anzahl der Primzahlen unter einer gegebenen Grösse nutzte Bernhard Riemann diese „strenge“ Funktionentheorie, um Primzahlen zu untersuchen. Die Schwierigkeit lag darin, der Reihe

$1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\cdots$

auch außerhalb ihres Konvergenzbereichs einen „quantitativen Sinn“ zu geben. Zuvor hatte Euler ebenfalls diese sogenannte Zeta-Funktion studiert, jedoch nur als formales Objekt und nicht über den komplexen Zahlen, weshalb ihm strenge Beweise, etwa für ihre Funktionalgleichung, verwehrt geblieben waren. Auch wurden die Unterschiede zwischen bedingter und absoluter Konvergenz herausgearbeitet. So zeigte Riemann im Jahr 1866 den Riemannschen Umordnungssatz. Auch konnten mit Hilfe der Reihen pathologische Beispiele in der Analysis konstruiert werden. Karl Weierstraß zeigte 1872, dass die Weierstraß-Funktion

$W(x):=\sum _{n=1}^{\mathrm{\infty }}{b}^n\cos (a^{n}x)$, mit $a\in {\mathbb{N}}_{>1}$ und $0<b<1$ mit $ab>1+\frac{3\pi }{2}$

in $ℝ$ zwar überall stetig, aber nirgends differenzierbar ist.

Die Theorie der divergenten Reihen wurde jedoch nicht gänzlich verworfen. War sie von Cauchy und Abel noch als „Erfindung des Teufels“ gebrandmarkt worden, lieferte ironischerweise der Abelsche Grenzwertsatz einen Grundstein für eine moderne und widerspruchsfreie Theorie der Limitierungsverfahren divergenter Reihen, die ab der zweiten Hälfte des 19. Jahrhunderts von Émile Borel und Ferdinand Georg Frobenius vorangetrieben wurde.

20. Jahrhundert bis heute

Im Laufe des 20. Jahrhunderts wurde unter anderem eine „strenge“ Theorie der divergenten Reihen, unter Vorbehalt gewisser Voraussetzungen, aufgebaut. Bei diesen Limitierungsverfahren wird, unter Berücksichtigung des quantitativen Verständnisses von Reihen, durch Limesbildung der Konvergenzbegriff verallgemeinert, sodass die Klasse „konvergenter Reihen“ ausgedehnt wird. Der Autodidakt Srinivasa Ramanujan hatte 1910 unter anderem durch die Behauptung

Srinivasa Ramanujan

„$1+2+3+4+5+6+\cdots =-\frac{1}{12}$“

für Aufmerksamkeit gesorgt, wobei neben weitestgehender Ablehnung (wegen der offensichtlichen Divergenz der Reihe zur linken Seite) der Brite Godfrey Harold Hardy darin eine korrekte „Auswertung“ des Funktionswertes $\zeta (-1)$ mit der Riemannschen Zeta-Funktion $\zeta (s):={\sum }_{n=1}^{\mathrm{\infty }}{n}^{-s}$ wiedererkannte (siehe auch Summe aller natürlichen Zahlen). Ramanujan hatte, ähnlich wie Leonhard Euler, eine gute Intuition für Limitierungsverfahren gehabt, und damit einige tiefgreifende Resultate vorhergesagt, ohne dafür strenge Beweise anzugeben. Zu seinen zahlreichen Entdeckungen gehörten Reihenformeln wie

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2+z^2+\frac{z^4}{n^2}}=\frac{\pi }{2z\sqrt{3}}\frac{\sinh (\pi z\sqrt{3})-\sqrt{3}\sin (\pi z)}{\cosh (\pi z\sqrt{3})-\cos (\pi z)}(z\notin e^{\pm \frac{\pi i}{3}}\mathbb{N})$

und auch

$\alpha \sum _{k=1}^{\mathrm{\infty }}\frac{\sinh (2\alpha nk)}{e^{2{\alpha }^{2}k}-1}+\beta \sum _{k=1}^{\mathrm{\infty }}\frac{\sin (2\beta nk)}{e^{2{\beta }^{2}k}-1}=\frac{\alpha \coth (\alpha n)}{4}-\frac{\beta \cot (\beta n)}{4}-\frac{1}{2}n(\alpha ,\beta ,n>0,\alpha \beta =\pi ,0<\beta n<\pi ).$

Dabei bezeichnen $\sinh ,\cosh ,\cot$ und $\coth$ den Sinus hyperbolicus, Cosinus hyperbolicus, Kotangens und den Kotangens hyperbolicus, $e$ bezeichnet die Eulersche Zahl.

Der Ramanujanexperte Bruce Berndt wies darauf hin, dass unter den Veröffentlichungen im 20. Jahrhundert, die durch Ramanujan vorhergesagte Formeln im Nachhinein bewiesen, ein Großteil zum Thema der unendlichen Reihen gehörte.

Konvergenzklassen in der Theorie der Limitierungsverfahren wurden als unterschiedlich groß erkannt. Zum Beispiel zeigte bereits Abel, dass, falls ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ konvergiert, auch der Grenzwert

$\underset{r\to 1^{-}}{\lim }\sum _{n=0}^{\mathrm{\infty }}{a}_n{r}^n=\sum _{n=0}^{\mathrm{\infty }}{a}_n$

existieren muss. Die Umkehrung dieses Resultats ist jedoch nicht richtig: Es existieren Reihen, die sich im obigen Sinne limitieren lassen mit divergenter Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$. Das Resultat Abels, das also eine Konvergenzklasse, nämlich die „klassische Konvergenz“, in eine größere Klasse einbettet, ist Spezialfall eines Abelschen Theorems. Sätze, die hinreichende Bedingungen für Umkehrungen von Abelschen Sätzen herausarbeiten, wurden durch Arbeiten von Alfred Tauber initiiert. Tauber zeigte, dass, falls $\underset{r\to 1^{-}}{\lim }{\sum }_{n=0}^{\mathrm{\infty }}{a}_n{r}^n$ existiert und $n{a}_n\to 0$, die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ konvergieren muss. Die sogenannten Tauber-Theoreme spielen bis heute in der Zahlentheorie, etwa beim Beweis des Primzahlsatzes, eine bedeutende Rolle. Besonders Godfrey Harold Hardy und John Edensor Littlewood griffen die Ideen Taubers auf und verallgemeinerten sie. Im Jahr 1949 erschien Hardys Buch mit dem Titel Divergent Series.

Auch in der Theorie der Fourierreihen wurden weitere Erfolge erzielt. 1923 konstruierte Andrei Nikolajewitsch Kolmogorow eine $L^1$-integrable Funktion, deren Fourierreihe fast überall divergiert. Dies widersprach Vermutungen seines Lehrers Nikolai Nikolajewitsch Lusin, der die punktweise Konvergenz solcher Fourierreihen vermutete. Für quadratintegrable Funktionen (Klasse $L^2$) vermutete man ebenfalls lange, dass sich Gegenbeispiele finden lassen würden, bis Lennart Carleson 1966 Lusins Vermutung für diese Klasse bewies.

Im weiteren Verlauf des 20. Jahrhunderts wurden Reihen verstärkt auch in formalen algebraischen Rahmen, also jenseits von Konvergenzfragen, als abstrakte Strukturen untersucht. So formen etwa die formalen Potenzreihen ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n{z}^n$ mit Koeffizienten $a_n\in R$ in einem Ring $R$ zusammen mit komponentenweiser Addition und dem Cauchyprodukt einen Ring $R[[z]]$. Häufig wird die Wahl $R=ℂ$ getroffen. In diesem Fall ist $ℂ[[z]]$ sogar faktoriell. Im Jahr 1959 konnten E. D. Cashwell und C. J. Everett zeigen, dass der Ring der formalen Dirichletreihen isomorph zu einem Potenzreihenring mit abzählbar vielen Veränderlichen, und damit insbesondere faktoriell, ist. Ferner erwies sich der „algebraische“ Umgang mit Reihen auch für die Kombinatorik von großem Nutzen. Diese Initiative wurde unter anderem von George Andrews seit den 1970er Jahren vorangetrieben, der zahlreiche kombinatorische Fragen, etwa zu den Partitionen, durch Reihenumformungen beantworten konnte, und an einem systematischen Ausbau der Theorie sogenannter „$q$-Reihen“ maßgeblich beteiligt war. Allerdings waren derartige Ansätze bereits zu den Zeiten Leonhard Eulers bekannt, der unter anderem den Pentagonalzahlensatz bewies.

Bis zum heutigen Tage sind Konvergenzfragen von Reihen von höchster Bedeutung und keinesfalls gelöst. So wird etwa die Riemannsche Vermutung, eines der sieben Millennium-Probleme, auf dessen Lösung der Preis von 1 Million US-Dollar ausgesetzt ist, von der Konvergenz der Reihe

$\sum _{n=1}^{\mathrm{\infty }}\frac{\mu (n)}{n^x}=1-\frac{1}{2^x}-\frac{1}{3^x}-\frac{1}{5^x}+\frac{1}{6^x}-\frac{1}{7^x}+\cdots$

für alle Werte $x>\frac{1}{2}$ impliziert. Dabei hängt die Möbiusfunktion $\mu (n)$ eng mit der Verteilung der Primzahlen zusammen. Bis dato ist lediglich Konvergenz für $x\ge 1$ und die Tatsache

$\sum _{n=1}^{\mathrm{\infty }}\frac{\mu (n)}{n}=0$

bekannt, was äquivalent zum Primzahlsatz ist.

Rechnen mit Reihen

Im Gegensatz zu gewöhnlichen (endlichen) Summen gelten für Reihen einige übliche Regeln der Addition nur bedingt. Man kann also nicht bzw. nur unter bestimmten Voraussetzungen mit ihnen wie mit endlichen Summenausdrücken rechnen. Es stellen sich grundsätzlich die Fragen:

• Wie kann man Reihen addieren, und wie wirkt sich das auf Konvergenz und Grenzwerte aus?
• Wie kann man Reihen multiplizieren, und wie wirkt sich das auf Konvergenz und Grenzwerte aus?

Summen und Vielfache

Man kann konvergente Reihen gliedweise addieren, subtrahieren oder mit einem festen Faktor (aber nicht einer anderen Reihe) multiplizieren (vervielfachen). Die resultierenden Reihen sind ebenfalls konvergent, und ihr Grenzwert ist die Summe bzw. Differenz der Grenzwerte der Ausgangsreihen bzw. das Vielfache des Grenzwertes der Ausgangsreihe. D. h.:

$\sum _{j=0}^{\mathrm{\infty }}(a_j\pm b_j)=\sum _{j=0}^{\mathrm{\infty }}{a}_j\pm \sum _{j=0}^{\mathrm{\infty }}{b}_j$

$\sum _{j=0}^{\mathrm{\infty }}A{a}_j=A\sum _{j=0}^{\mathrm{\infty }}{a}_j$.

Produkte

Man kann absolut konvergente Reihen gliedweise miteinander multiplizieren. Die Produktreihe ist ebenfalls absolut konvergent und ihr Grenzwert ist das Produkt der Grenzwerte der Ausgangsreihen. D. h.:

$\sum _{j,k=0}^{\mathrm{\infty }}(a_j{b}_k)=\left(\sum _{j=0}^{\mathrm{\infty }}{a}_j\right)\cdot \left(\sum _{k=0}^{\mathrm{\infty }}{b}_k\right)$

Da die Schreibweise (auf der linken Seite der Gleichung) der Produktreihe mit zwei Indizes in bestimmten Zusammenhängen „unhandlich“ ist, wird die Produktreihe auch in Form des Cauchyprodukts geschrieben. Der Name ergibt sich daraus, dass die Glieder der Produktreihe mit Hilfe des Cauchyschen Diagonalverfahrens gebildet werden, dabei werden die Glieder der Ausgangsfolgen in einem quadratischen Schema paarweise angeordnet, und die (durchnummerierten) Diagonalen dieses Schemas bilden die Produktglieder. Für die Produktreihe braucht man dann nur noch einen einzelnen Index. Die Produktreihe hat dann die folgende Form:

$\sum _{j,k=0}^{\mathrm{\infty }}(a_j{b}_k)=\sum _{n=0}^{\mathrm{\infty }}(a_0{b}_n+a_1{b}_{n-1}+\cdots +a_{n-1}{b}_1+a_n{b}_0)=\sum _{n=0}^{\mathrm{\infty }}\underset{:=c_n}{\underbrace{\left(\sum _{m=0}^n{a}_m{b}_{n-m}\right)}}$

Der Satz von Mertens besagt, dass das Produkt $\sum c_n$ beider Reihen $\sum a_j$ und $\sum b_k$ auch noch dann gegen das Produkt der Grenzwerte konvergiert, wenn mindestens eine der beiden Reihen absolut konvergiert. Es konvergiert die Reihe ${\sum }_{k=0}^{\mathrm{\infty }}{c}_k$ mit $c_k={\sum }_{j=0}^k{a}_j{b}_{k-j}$ genau dann für alle konvergenten ${\sum }_{k=0}^{\mathrm{\infty }}{b}_k$, falls ${\sum }_{k=0}^{\mathrm{\infty }}{a}_k$ absolut konvergiert.

Anwendungen haben Reihenprodukte zum Beispiel beim Nachweis von Funktionalgleichungen. Setzt man etwa

$\exp (x):=\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\cdots ,$

so konvergiert die betroffene Reihe für alle $x\in ℝ$ absolut. Mit dem binomischen Lehrsatz erhält man für $a_j:=\frac{x_1^j}{j!}$ und $b_k:=\frac{x_2^k}{k!}$:

$c_n=\sum _{k=0}^n{a}_k{b}_{n-k}=\sum _{k=0}^n\frac{x_1^k{x}_2^{n-k}}{k!(n-k)!}=\frac{1}{n!}\sum _{k=0}^n\frac{n!}{k!(n-k)!}{x}_1^k{x}_2^{n-k}=\frac{(x_1+x_2{)}^n}{n!}.$

Damit folgt mit dem Cauchyprodukt für alle $x_1,x_2\in ℝ$

$\exp (x_1)\exp (x_2)=\exp (x_1+x_2),$

was die Funktionalgleichung der Exponentialfunktion ist.

Rechnen innerhalb der Reihe

Klammerung (Assoziativität)

Man kann innerhalb einer konvergenten Reihe die Glieder beliebig durch Klammern zusammenfassen. Man kann also beliebig viele Klammern in den „unendlichen Summenausdruck“ einfügen, man darf sie nur nicht innerhalb eines (aus mehreren Termen zusammengesetzten) Gliedes setzen. Der Wert der Reihe ändert sich durch die zusätzlich eingefügte Klammerung dann nicht.

Dies gilt für divergente Reihen im Allgemeinen nicht, was man leicht am folgenden Beispiel erkennt: Die Reihe

$\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k=1-1+1-1+\cdots$

divergiert, während die beklammerte Reihe

$\sum _{k=0}^{\mathrm{\infty }}((-1{)}^{2k}+(-1{)}^{2k+1})=(1-1)+(1-1)+\cdots =0+0+\cdots =0$

gegen Null konvergiert und die anders beklammerte Reihe

$1+\sum _{k=1}^{\mathrm{\infty }}((-1{)}^{2k-1}+(-1{)}^{2k})=1+(-1+1)+(-1+1)+\cdots =1+0+0+\cdots =1$

gegen noch eine andere Zahl konvergiert.

Andererseits kann man aber keine Klammern ohne Weiteres weglassen. Man kann das aber immer dann, wenn die resultierende Reihe wieder konvergent ist. In diesem Falle bleibt auch der Reihenwert unverändert: Sind die Glieder $A_k$ einer konvergenten Reihe ${\sum }_{k=0}^{\mathrm{\infty }}{A}_k$ selbst in Summenform $A_k=a_{{\nu }_k+1}+\cdots +a_{{\nu }_{k+1}}$ (mit $k=0,1,\dots$ und ${\nu }_0=-1$), so „darf“ man die sie umschließenden Klammern genau dann weglassen, wenn die dadurch entstehende neue Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ wieder konvergiert.

Umordnung (Kommutativität)

Eine Umordnung einer Reihe wird durch eine Permutation ihrer Indexmenge dargestellt. Ist die Indexmenge zum Beispiel die Menge ${\mathbb{N}}_0$ der natürlichen Zahlen mit Null und $\sigma :{\mathbb{N}}_0\to {\mathbb{N}}_0,k\mapsto \sigma (k)$ eine bijektive Abbildung der natürlichen Zahlen auf sich, so heißt

$\sum _{k=0}^{\mathrm{\infty }}{a}_{\sigma (k)}$

eine Umordnung der Reihe

$\sum _{k=0}^{\mathrm{\infty }}{a}_k.$

Man kann konvergente Reihen unter Beibehaltung ihres Wertes dann und nur dann beliebig umordnen, wenn sie unbedingt bzw. absolut konvergent sind. Es gilt für unbedingt (oder absolut) konvergente Reihen:

$\sum _{k=0}^{\mathrm{\infty }}{a}_k=\sum _{k=0}^{\mathrm{\infty }}{a}_{\sigma (k)}$ für alle bijektiven $\sigma :{\mathbb{N}}_0\to {\mathbb{N}}_0$.

Bedingt konvergente Reihen dürfen zur Erhaltung des Grenzwerts nur endlich umgeordnet werden, d. h. ab einem gewissen Index muss für die Umordnung $\sigma (k)=k$ gelten. Der Riemannsche Umordnungssatz sagt aus, dass durch geeignete Umordnung einer fixierten, bedingt konvergenten Reihe reeller Zahlen jeder reelle Grenzwert erreicht werden kann.

Reihen von Funktionen

Allgemeines

Ein zentrales Problem der Analysis besteht darin, „komplizierte“ Funktionen zu studieren. Dabei bedeutet „kompliziert“ zum Beispiel, dass die Rechenvorschrift nicht aus einer endlichen Abfolge aus Anwendungen der vier Grundrechenarten besteht. Eine in diesem Sinne „einfache“ Vorschrift wäre: Nimm die Eingangszahl mal Zwei, dann das Ergebnis plus Eins, multipliziere dies mit sich selbst, teile dann alles durch die Drei. In Kurzform: $x\mapsto \frac{1}{3}(2x+1{)}^2$. Jedoch lassen sich sehr viele Phänomene in der Natur nicht so einfach beschreiben. Die Mathematik ist demnach bestrebt, Analyseverfahren nichttrivialer Funktionen zu entwickeln. Solche Verfahren kommen in den unterschiedlichsten Bereichen innerhalb der Mathematik und auch ihrer Anwendungen zum Einsatz.

Haben die betrachteten Funktionen Zielmengen $B$, in denen nicht gerechnet werden kann, so ist keine Darstellung als unendliche Reihe möglich.

Eine naheliegende Möglichkeit, „komplizierte“ Funktionen $f(x)$ zu konstruieren und untersuchen, ist, sie als Reihe von Funktionen $f_n(x)$ zu schreiben, wobei jeder einzelne Summand in der Praxis „einfache Eigenschaften“ besitzt:

$f(x):=\sum _{n=1}^{\mathrm{\infty }}{f}_n(x)=f_1(x)+f_2(x)+f_3(x)+\cdots .$

Anstatt also Folgen von Zahlen kann man auch Folgen von Funktionen betrachten und entsprechend Reihen definieren. Zudem ist zu beachten, dass im Darstellungsbereich alle $f_n$ notwendigerweise an allen Stellen $x$ aus dem Definitionsbereich von $f$ definiert sein müssen. Ferner muss im Zielbereich der Funktionen $f,f_1,f_2,\dots$ die Addition von Termen definiert sein, da sonst keine sinnvolle Reihe gebildet werden kann.

Eigenschaften der Grenzfunktionen

Im Falle der Konvergenz einer Funktionenreihe kommt noch die Frage nach den Eigenschaften der Grenzfunktion $f$ auf. Meistens wird gefragt: „Falls die $f_n$ einzeln betrachtet alle stetig/differenzierbar/integrierbar sind, ist es auch die Funktion $f$?“ Antworten bzw. hinreichende Entscheidungskriterien auf diese Fragen liefern Sätze aus der Analysis. Häufig nützt es zum Beispiel, wenn die Funktionenreihe nicht nur in jedem Punkt gegen die Grenzfunktion konvergiert, sondern im Definitionsbereich sogar gleichmäßige Konvergenz vorliegt. In einem solchen Fall ist, falls die $f_n$ alle stetige Funktionen waren, auch die Grenzfunktion stetig. Ähnliche Voraussetzungen gelten für Beschränktheit (falls alle Partialsummen beschränkt sind), Differenzierbarkeit und Integrierbarkeit der Grenzfunktion, falls alle Summanden die entsprechenden Eigenschaften haben.

Vertauschen von Reihen mit Differentialoperator und Integral

Im Gebiet $[a,b]$ der gleichmäßigen Konvergenz darf eine Reihe gliedweise integriert werden:

$\underset{t_0}{\overset{t}{\int }}\sum _{n=1}^{\mathrm{\infty }}{f}_n(x)\mathrm{d}x=\sum _{n=1}^{\mathrm{\infty }}\underset{t_0}{\overset{t}{\int }}{f}_n(x)\mathrm{d}x,t_0,t\in [a,b].$

Ebenso darf sie gliedweise differenziert werden, sofern die entstehende Reihe gleichmäßig konvergiert:

$(\sum _{n=1}^{\mathrm{\infty }}{f}_n(x))=\sum _{n=1}^{\mathrm{\infty }}{f_n}^{\prime }(x),x\in [a,b].$

Da Differenzierbarkeit eine lokale Eigenschaft ist, kann dies unter Ausschöpfen offener Bereiche durch kompakte Mengen gegebenenfalls auch auf allgemeinere Funktionen ausgeweitet werden.

In einigen Anwendungen stellen die oberen Kriterien beim Vertauschen von Summe und Integral jedoch zu große Hürden dar. Zum einen decken sie nicht Maßräume unendlichen Volumens ab (wie zum Beispiel Intervalle wie $ℝ$ oder $[0,\mathrm{\infty })$ mit dem eindimensionalen Lebesgue-Maß), zum anderen kann die Forderung nach gleichmäßiger Konvergenz große Schwierigkeiten mit sich bringen. Mit Resultaten aus der Funktionalanalysis, wie dem Satz von Fischer-Riesz, können jedoch weit allgemeinere Aussagen erzielt werden, die allerdings auch deutlich schwerer zu beweisen sind. Einer davon ist der Satz über die gliedweise Integration von Reihen: Ist $(E,||\cdot |{|}_E)$ ein Banachraum (zum Beispiel $E=ℝ,ℂ$) und $(f_j{)}_{j\in {\mathbb{N}}_0}:X\to E$ eine Folge in ${ℒ}^1(X,𝒜,\mu )$ (wobei $\mu$ ein Maß auf $X$ und $𝒜$ eine zugehörige $\sigma$-Algebra des Raumes $X$ ist), und gilt

$\sum _{j=0}^{\mathrm{\infty }}\underset{X}{\int }||f_j|{|}_E\mathrm{d}\mu <\mathrm{\infty }$,

so ist ${\sum }_{j=0}^{\mathrm{\infty }}{f}_j$ $\mu$-fast überall absolut konvergent und $\mu$-integrierbar. Es gilt zudem

$\sum _{j=0}^{\mathrm{\infty }}\underset{X}{\int }{f}_j\mathrm{d}\mu =\underset{X}{\int }\left(\sum _{j=0}^{\mathrm{\infty }}{f}_j\right)\mathrm{d}\mu .$

Dies ist eine Folgerung aus dem Satz von der majorisierten Konvergenz. Zu beachten ist, dass dieser sehr allgemeine Satz gänzlich auf Forderungen wie gleichmäßige Konvergenz verzichtet. Unter Benutzung der ${\ell }^1$-Folgenräume sowie des Zählmaßes ist ein Spezialfall, dass unter Voraussetzung von ${\sum }_{j=0}^{\mathrm{\infty }}{\sum }_{k=0}^{\mathrm{\infty }}|a_{j,k}|<\mathrm{\infty }$ bereits Konvergenz der Doppelreihe und zudem

$\sum _{j=0}^{\mathrm{\infty }}\sum _{k=0}^{\mathrm{\infty }}{a}_{j,k}=\sum _{k=0}^{\mathrm{\infty }}\sum _{j=0}^{\mathrm{\infty }}{a}_{j,k}$

folgt.

Es existieren jedoch auch Anwendungen, in denen weder gleichmäßige Konvergenz von ${\sum }_{j=0}^{\mathrm{\infty }}{f}_j$ noch Integrierbarkeit der oben gewählten „Majorante“ ${\sum }_{j=0}^{\mathrm{\infty }}||f_j||$ vorliegt. In solchen Fällen kann der Satz von der majorisierten Konvergenz unter Umständen dennoch einen Ausweg darstellen, wobei jedoch die Einzelfälle genauer betrachtet werden müssen. Es ist lediglich notwendig, die Partialsummen ${\sum }_{j=0}^n{f}_j$ der zu integrierenden punktweise konvergenten Funktionenreihe durch eine integrierbare und von $n$ unabhängige Majorante nach oben abzuschätzen, wobei aber manchmal auf die gegebenenfalls zu grobe Dreiecksungleichung verzichtet werden kann. Ein Beispiel ist der Beweis der Leibnizreihe

$\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{2k+1}=\frac{\pi }{4}$

durch Integrale. Jeder der Terme $\frac{(-1{)}^k}{2k+1}$ erfüllt

$\frac{(-1{)}^k}{2k+1}=\underset{0}{\overset{1}{\int }}(-1{)}^k{x}^{2k}\mathrm{d}x.$

Allerdings ist die Reihe ${\sum }_{k=0}^{\mathrm{\infty }}(-1{)}^k{x}^{2k}$ im Intervall $[0,1)$ zwar punktweise konvergent, aber weder gleichmäßig konvergent, noch ist die absolute „Majorante“ ${\sum }_{k=0}^{\mathrm{\infty }}{x}^{2k}=\frac{1}{1-x^2}$ auf $[0,1)$ integrierbar, weshalb die Dreiecksungleichung nicht verwendet werden kann. Mit der feineren Abschätzung alternierender Reihen werden jedoch die Vorzeichenwechsel berücksichtigt, und es ergibt sich mit der Monotonie der Folge $x^{2k}$

$|\sum _{k=0}^n(-1{)}^k{x}^{2k}|\le 1$

für alle $n$ und $0\le x<1$. Da $1$ offenbar über $[0,1)$ absolut integrierbar ist, darf Summation und Integration vertauscht werden:

$\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{2k+1}=\sum _{k=0}^{\mathrm{\infty }}\underset{[0,1)}{\int }(-1{)}^k{x}^{2k}\mathrm{d}x=\underset{[0,1)}{\int }\frac{\mathrm{d}x}{x^2+1}=\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}x}{x^2+1}=\arctan (1)-\arctan (0)=\frac{\pi }{4}.$

Hierbei bezeichnet $\arctan$ den Arkustangens.

Holomorphe Grenzfunktionen

Es gibt auch hinreichende Kriterien für die Holomorphie der Grenzfunktion. Genauer lässt sich der Weierstraßsche Konvergenzsatz auf unendliche Reihen anwenden: Ist $f_n:U\to ℂ$ eine Folge holomorpher Funktionen, so konvergiert $f={\sum }_{n=1}^{\mathrm{\infty }}{f}_n$ gegen eine holomorphe Funktion $f:U\to ℂ$, falls sie in $U$ normal konvergiert, d. h. für jeden Punkt $z\in U$ gibt es eine Umgebung $z\in V\subset U$, sodass

$\sum _{n=1}^{\mathrm{\infty }}\underset{w\in V}{\sup }|f_n(w)|<\mathrm{\infty }.$

Typen von Funktionenreihen

Man kann fragen, ob und durch welche Reihe sich eine Funktion darstellen lässt. So eine Darstellung nennt sich Reihenentwicklung. Es existieren je nach Kontext verschiedene relevante Reihenentwicklungen für gewisse Klassen von Funktionen.

Potenzreihen, Taylorreihen und analytische Funktionen

Bei analytischen Funktionen wird eine Funktion um einen „Definitionspunkt“ herum über Polynome angenähert. Eine Möglichkeit, dies zu realisieren und zu verstehen, besteht darin, die Funktion zunächst sehr stark einzuschränken, also nur Eingabewerte aus einem sehr „kleinen“ Vorrat einzusetzen. Klein bedeutet in diesem Zusammenhang, dass die betrachteten Eingabewerte sehr nahe beieinander liegen. Soll eine Funktion etwa um 0 herum studiert werden, würden Werte wie 0,000001 vielleicht noch in Betracht gezogen, möglicherweise aber nicht mehr 1, geschweige denn 100. In diesem Zusammenhang nennt man die 0 auch den Entwicklungspunkt. Hinter diesem Prinzip steckt eine gewisse Form der „Stetigkeit“: Wurde eine analytische Funktion im Punkt 0 gut verstanden, so lässt sich daraus schon auf ihr Verhalten in zum Beispiel 0,000001 schließen, und das nur anhand der vier Grundrechenarten. Präziser wird die Annäherung über Polynome realisiert, also Ausdrücke wie $x+2$, $x^3-4x^2+3x-1$ und ganz allgemein

$a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_0.$

Eine analytische Funktion kann also um jeden Wert ihres Definitionsbereichs durch Anwendung der Grundrechenarten entwickelt werden. Dabei ist zu beachten, dass es sich bei hinreichend „komplizierten“ Funktionen nur um eine Näherung handelt. Eine zentrale Eigenschaft der Analytizität ist aber, dass für solche komplizierten Funktionen beliebig lange Polynomketten, also addierte $x^n$-Terme, zur Annäherung gefunden werden können. Je länger diese Terme sind, desto besser. Lässt man diesen Prozess gegen Unendlich streben, ist die Annäherung in den umliegenden Punkten perfekt, es herrscht also Gleichheit. In diesem Sinne sind also analytische Funktionen, zumindest lokal, gerade „unendlich lange Polynome“. Diese werden auch als Potenzreihen bezeichnet. Obwohl dabei unendlich viele Terme addiert werden, kann Konvergenz vorliegen, wenn das Funktionsargument nahe genug am Entwicklungspunkt liegt. Wählt man zum Beispiel den Entwicklungspunkt 0 und für die Koeffizienten die Dezimalstellen der Kreiszahl $\pi$, also

$f(x):=3+x+4x^2+x^3+5x^4+9x^5+2x^6+6x^7+\cdots ,$

so gilt

$f\left(\frac{1}{10}\right)=3+\frac{1}{10}+\frac{4}{100}+\frac{1}{1000}+\frac{5}{10000}+\cdots =3,1415926\dots =\pi .$

Für Werte $|x|<\frac{1}{10}$ wird dann $f(x)$ „erst recht“ endlich sein. Diesem Gedanken folgend kann man etwa über das Majorantenkriterium (siehe unten) zeigen, dass Potenzreihen entweder überall oder innerhalb von Intervallen (für komplexe Zahlen Kreisscheiben) mit dem Entwicklungspunkt als Zentrum konvergieren.

Über das Beispiel des Sinus erklärt sich auch das allgemeine Verfahren zum Aufstellen einer Taylorreihe zu einer analytischen Funktion $f(x)$. Wird als Entwicklungspunkt $x_0$ gewählt, so gilt die Formel

$f(x)=\sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n,$ mit $f^{(n)}(x_0)=n$-te Ableitung von $f$ an der Stelle $x_0$,

für alle $x$, die nahe genug an $x_0$ liegen. Dabei bezeichnet $f^{(n)}(x_0)$ die $n$-te Ableitung von $f$ an der Stelle $x_0$. Genau genommen muss $|x-x_0|<R$ gelten, wobei die Zahl $R$ den Konvergenzradius der Taylorreihe bezeichnet. Ist der Entwicklungspunkt $x_0=0$, spricht man gelegentlich auch von einer Maclaurinschen Reihe. Sind auch negative ganzzahlige Exponenten von $(x-x_0)$ vorhanden, verallgemeinert sich das Konzept zu Laurent-Reihen.

Beispiel: Approximation der Zahl $\sqrt{26}$

Taylorentwicklungen lassen sich zum Beispiel an der Wurzelfunktion $x\mapsto \sqrt{x}$ demonstrieren, etwa um den Punkt $c=25$. Diese ist dort analytisch, man hat die Ableitungen $(\sqrt{x}{)}^{\prime }=\frac{1}{2\sqrt{x}}$ und $(\sqrt{x}{)}^{″}=-\frac{1}{4{\sqrt{x}}^3}$. Also gilt mit der Taylor-Formel die Approximation $\sqrt{x}\approx \sqrt{25}+\frac{1}{2\sqrt{25}}(x-25)-\frac{1}{8\cdot {\sqrt{25}}^3}(x-25{)}^2=5+\frac{1}{10}(x-25)-\frac{1}{1000}(x-25{)}^2$ für Zahlen $x$, die nahe an $25$ liegen. Der Ausdruck $5+\frac{1}{10}(x-25)-\frac{1}{1000}(x-25{)}^2$ auf der rechten Seite kann, wie oben, durch Anwendung nur der vier Grundrechenarten schnell berechnet werden. Er stimmt nach Einsetzen von $x=25$ exakt mit dem Funktionswert $5$ überein, doch auch in der näheren Umgebung von $25$ ist die Annäherung noch sehr genau. Man hat etwa $\sqrt{26}\approx 5+\frac{1}{10}-\frac{1}{1000}=5,099$ und es gilt für den exakten Wert $\sqrt{26}=5,0990195\dots$.

Die Theorie der analytischen Funktionen wird erst über den komplexen Zahlen vollständig erfassbar. Hier spricht man synonym von holomorphen Funktionen und es gilt der Cauchysche Entwicklungssatz: Ist $c\in U$ mit offenem $U$, $B_r(c)$ die größte Kreisscheibe um $c$ in $U$ und $f:U\to ℂ$ holomorph, so ist $f$ um $c$ in eine Taylorreihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n(z-c{)}^n$ entwickelbar, die in $B_r(c)$ auf kompakten Teilmengen absolut und gleichmäßig konvergiert. Die Koeffizienten sind gegeben durch

$a_n=\frac{f^{(n)}(c)}{n!}=\frac{1}{2\pi i}{\oint }_{\partial B_d(c)}\frac{f(w)}{(w-c{)}^{n+1}}\mathrm{d}w$, wobei $0<d<r.$

Dabei wird der Integrationsweg in mathematisch positiver Richtung einfach durchlaufen. Bemerkenswert ist die Tatsache, dass für den Beweis des Entwicklungssatzes lediglich die Reihenentwicklungen der Funktionen $z\mapsto (z-c{)}^{-k-1}$ benötigt werden (siehe auch geometrische Reihe) sowie Vertauschbarkeit von Summation und Integration. Für den Fall $k=0$ wurde dies bereits 1831 von Cauchy durchgeführt.

Da jede holomorphe Funktion analytisch ist und umgekehrt, lassen sich Eigenschaften von Potenzreihen direkt auf holomorphe Funktionen übertragen. Dies stellt gleichzeitig den Weierstraßschen Zugang zur Funktionentheorie dar, der die Darstellbarkeit von Funktionen als Potenzreihen zum Ausgangspunkt hat.

Potenzreihen können auch als sog. Lambertreihen geschrieben werden.

Fourierreihen

Als Fourierreihe einer Funktion bezeichnet man ihre Entwicklung nach trigonometrischen Funktionen. Dies betrifft vornehmlich periodische Funktionen, also Funktionen, die sich intervallweise immer wieder in ihrem Abbildungsverhalten wiederholen. Da eine Normierung der Periode durch entsprechende Skalierung im Funktionsargument erreicht werden kann, genügt es, sich $1$-periodische Funktionen anzuschauen, also solche mit der Eigenschaft $f(x+1)\equiv f(x)$.

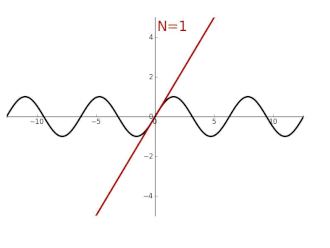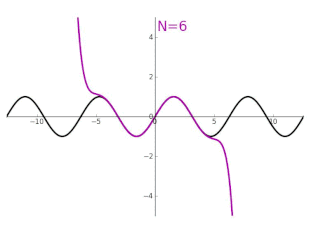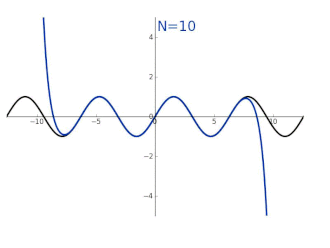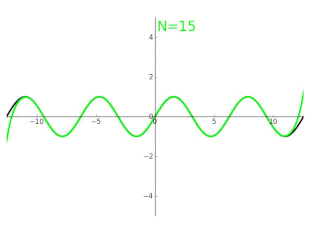
Fourierreihen spielen eine Rolle bei der Überlagerung von Wellen, zum Beispiel bei der Erzeugung von Klängen. Erklingen mehrere Töne gleichzeitig, etwa bei einem Musikstück, so entspricht dies physikalisch einer Überlagerung verschiedener Schallwellen. Um die Gesamtsituation zu erfassen, ist die Addition der entsprechenden (nach Phase und Amplitude skalierten) Sinuskurven erforderlich. Gewisse periodische Signale, zum Beispiel in der Elektrotechnik, haben jedoch ein derart komplexes Muster, dass eine unendliche Anzahl verschiedener Sinuswellen benötigt wird, um sie exakt darzustellen.

Animation der Approximation des Sägezahnsignals durch sich überlappende Sinuskurven

Ist eine $1$-periodische Funktion, etwa ein Signal, gegeben, so ist eine Entwicklung in eine Fourierreihe (zumindest formal) dann möglich, wenn $f$ auf dem Interval $[0,1]$ integrierbar ist. In diesem Fall macht es Sinn, den $n$-ten Fourierkoeffizienten über die Formel

$a_n:=\underset{0}{\overset{1}{\int }}f(x)e^{-2\pi inx}\mathrm{d}x=\underset{0}{\overset{1}{\int }}f(x)\cos (2\pi nx)\mathrm{d}x-i\underset{0}{\overset{1}{\int }}f(x)\sin (2\pi nx)\mathrm{d}x$

zu definieren. Es ist dabei die Eulersche Identität $e^{i\varphi }=\cos (\varphi )+i\sin (\varphi )$ zu beachten, die den entscheidenden Zusammenhang zwischen der komplexen Exponentialfunktion und den trigonometrischen Funktionen herstellt. Da $f$ $1$-periodisch ist, sollten diese Integrale „alle Daten“ von $f$ beinhalten. Die Aussage ist nun, dass die Kollektion der Koeffizienten $a_n$ mit $n\in \mathbb{Z}$ unter Umständen ausreicht, das gesamte Signal $f$ vollständig zu rekonstruieren. Dies wird über die Konvergenz der zunächst nur formalen Fourierreihe

$f(x)\sim \sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_n{e}^{2\pi inx}$

realisiert. Ist zum Beispiel $f$ stetig differenzierbar, so wird die zugehörige Fourierreihe gleichmäßig gegen $f$ konvergieren. Allgemein bezeichnet man Kriterien, die Konvergenz(arten) von Fourierreihen festlegen, auch als Dirichlet-Bedingungen. Zum Beispiel verrät das Verhalten der Funktion einiges über die Fourierkoeffizienten: Wenn eine 1-periodische Funktion $f(x)$ mit ihren Ableitungen bis zur $k$-ten Ordnung stetig ist, dann streben für $|n|\to \mathrm{\infty }$ die Terme $a_n{n}^{k+1}$ gegen Null. Ist umgekehrt $f$ stetig und konvergiert ${\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}|n||a_n|$, so ist $f$ bereits stetig differenzierbar und es gilt $\underset{N\to \mathrm{\infty }}{\lim }{\sum }_{n=-N}^{N}2\pi in{a}_n{e}^{2\pi inx}=f^{\prime }(x)$.

Es kann die Fourierreihe zu $f$ auch ausschließlich in Termen von Sinus und Kosinus ohne komplexe Zahlen statt der Exponentialfunktion ausgedrückt werden, wobei die Wellenüberlagerung ersichtlicher wird. Allerdings ist die Nutzung komplexer Zahlen in der Elektrotechnik, auch im Kontext von Wellen, durchaus üblich.

Fourierreihen können auch im Komplexen betrachtet werden. Ist $f$ auf dem offenen Streifen

$D=\{z\in ℂ\mid a<\mathrm{Im}(z)<b\},$

holomorph und $1$-periodisch, gilt also stets $f(z+1)=f(z)$, so besitzt $f$ eine Fourier-Entwicklung

$f(z)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_n{e}^{2\pi izn}.$

Dies ist auf ganz $D$ absolut und lokal gleichmäßig konvergent. Eine Berechnung der Koeffizienten ist für jedes $a<y<b$ durch

$a_n=\underset{0}{\overset{1}{\int }}f(x+iy)e^{-2\pi in(x+iy)}\mathrm{d}x$

möglich. Entscheidend für die Herleitung der Existenz einer Fourierreihe auf horizontalen Streifen ist das Abbildungsverhalten der komplexen Exponentialfunktion $z\mapsto e^{2\pi iz}$ sowie die Existenz der Laurent-Reihe. Die Entwicklung holomorpher Funktionen in Fourierreihen spielt zum Beispiel eine große Rolle in der Theorie der Modulformen.

Dirichletreihen

Dirichletreihen kommen vor allen Dingen in der Zahlentheorie zum Einsatz. Damit ist die Teildisziplin der Mathematik gemeint, die sich mit den Eigenschaften ganzer und auch rationaler Zahlen befasst. Viele Fragestellungen, etwa aus der multiplikativen Zahlentheorie, hängen dabei mit Primfaktorzerlegungen zusammen. An diesem Punkt kommen Dirichletreihen ins Spiel. Diese ahmen in manchen Fällen Primfaktorzerlegungen nach und übertragen dieses zahlentheoretische Element damit direkt in die Funktionentheorie.

Als Dirichletreihe bezeichnet man eine Entwicklung

$F(s)=\sum _{n=1}^{\mathrm{\infty }}\frac{a_n}{n^s}$ mit $s=\sigma +it\in ℂ.$

In gewisser Weise handelt es sich um eine „Potenzreihe unter Vertauschung der Rollen“: Bei Dirichletreihen wird über die Basis der Potenz $n^{-s}$ summiert und nicht über den Exponenten, wie es bei $x^n$ in Potenzreihen noch der Fall war. Während Potenzreihen im Komplexen auf Kreisscheiben konvergieren, konvergieren Dirichletreihen im Komplexen auf rechten Halbebenen. Ist eine Dirichletreihe zudem in einem Punkt $s_0$ konvergent, so ist sie in jedem Punkt $s_0+1+\delta$ mit $\delta >0$ absolut konvergent. Der Bereich der absoluten Konvergenz ist wieder eine Halbebene, die von der Halbebene der Konvergenz umschlossen wird.

Die sich aus den Potenzgesetzen ergebende Rechenregel $m^{-s}{n}^{-s}=(mn{)}^{-s}$ macht Dirichletreihen für die Zahlentheorie interessant. Sind nämlich die Koeffizienten $a_n$ ebenfalls (stark) multiplikativ, gilt also $a_m{a}_n=a_{mn}$ so existiert im Bereich der absoluten Konvergenz das Euler-Produkt

$F(s)=\prod _{p\text{Primzahl}}\frac{1}{1-a_p{p}^{-s}}=\frac{1}{1-a_2\cdot 2^{-s}}\times \frac{1}{1-a_3\cdot 3^{-s}}\times \frac{1}{1-a_5\cdot 5^{-s}}\times \cdots .$

Kann die Funktion $F(s)$, ähnlich wie ein Polynom, auch über ihre Nullstellen in ein Produkt faktorisiert werden, können damit Verbindungen zwischen Primzahlen und Eigenschaften von Nullstellen spezieller Funktionen aufgebaut werden. Dies betrifft zum Beispiel die Riemannsche Zeta-Funktion

$\zeta (s)=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^s}=\prod _{p\text{Primzahl}}\frac{1}{1-p^{-s}}(\sigma >1),$

deren Nullstellen in Dualität zur Folge der Primzahlen steht. Die Lage der Nullstellen in der komplexen Ebene ist Gegenstand der Riemannschen Vermutung. Eine ähnlich tiefe Vermutung, die Vermutung von Birch und Swinnerton-Dyer, befasst sich ebenfalls mit Nullstellen von Dirichletreihen, die ein Euler-Produkt besitzen. Eine sehr weitreichende Verallgemeinerung findet die Riemannsche Zeta-Funktion in den L-Funktionen.

Partialbruchzerlegungen und elliptische Funktionen

In der komplexen Ebene können manche Funktionen durch „Interpolation ihrer Singularitäten“ generiert werden. Dies trifft auf rationale Funktionen zu, kann aber in einigen Fällen durch unendliche Reihen ausgedehnt werden. Ist $f$ eine ganze Funktion, die für Konstanten $C,\varrho >0$ stets die Ungleichung

$|f(z)|<C{e}^{\varrho |\mathrm{Im}(z)|}$

erfüllt, so gilt bereits

$\frac{\mathrm{d}}{\mathrm{d}z}\left(\frac{f(z)}{\sin (\varrho z)}\right)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\varrho (-1{)}^{n+1}f\left(\frac{\pi n}{\varrho }\right)}{(\varrho z-n\pi {)}^2}.$

Ist $f$ zusätzlich eine ungerade Funktion, ist also stets $f(-z)=-f(z)$, gilt

$\frac{f(z)}{2\varrho z\cos (\varrho z)}=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^{n}f(\frac{\pi (n+\frac{1}{2})}{\varrho })}{(\pi (n+\frac{1}{2}){)}^2-{\varrho }^2{z}^2}.$

Für $f(z)=\sin (\pi z)$ führt dies, nach einem Shift im Argument, zur Partialbruchzerlegung des Kotangens:

$\pi \cot (\pi z)=\frac{1}{z}+\sum _{n=1}^{\mathrm{\infty }}[\frac{1}{z+n}+\frac{1}{z-n}].$

Dieses Konzept lässt sich auf Gitter ausweiten. Seien ${\omega }_1,{\omega }_2\in ℂ\setminus \{0\}$ zwei komplexe Zahlen, die über $ℝ$ linear unabhängig sind und sei $\mathrm{\Lambda }:=\{m{\omega }_1+n{\omega }_2:m,n\in \mathbb{Z}\}$ das Gitter, das von ${\omega }_1$ und ${\omega }_2$ erzeugt wird. Dann ist die Weierstraßsche $\mathrm{\wp }$-Funktion zum Gitter $\mathrm{\Lambda }$ wie folgt definiert:

$\mathrm{\wp }(z,\mathrm{\Lambda }):=\frac{1}{z^2}+\sum _{\lambda \in \mathrm{\Lambda }\setminus \{0\}}(\frac{1}{(z-\lambda {)}^2}-\frac{1}{{\lambda }^2}).$

Die Reihe konvergiert lokal gleichmäßig absolut in $ℂ\setminus \mathrm{\Lambda }$. Es handelt sich um eine doppelperiodische, also elliptische Funktion. Eng verwandt zu den elliptischen Funktionen sind die sog. Eisensteinreihen.

Konvergenzkriterien

Zwar gibt es kein brauchbares, allgemeingültiges Kriterium, um zu entscheiden, ob eine Reihe konvergiert, aber in manchen Spezialfällen lassen sich unter zusätzlichen Annahmen Kriterien angeben, die auf ganz unterschiedlichen mathematischen Techniken basieren.

Allgemeine Kriterien

Nullfolgenkriterium

Vorlage:Hauptartikel Wenn die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ konvergiert, dann konvergiert die Folge $a_n$ der Summanden für $n\to \mathrm{\infty }$ gegen 0. Kontraponiert: Ist $a_n$ keine Nullfolge, so divergiert die entsprechende Reihe.

Zudem gilt der Satz von Olivier: Ist $a_n$ monoton fallend und ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ konvergent, so folgt bereits $n{a}_n\to 0$.

Beispiel

Es kann die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}(-1{)}^n=1-1+1-1+\cdots$ (trotz beschränkter Partialsummen) nicht konvergieren, da $a_n=(-1{)}^n$ nicht gegen 0 konvergiert.

Die Umkehrung ist nicht allgemeingültig (ein Gegenbeispiel ist die harmonische Reihe). Das Nullfolgenkriterium wird daher in erster Linie zum Nachweis der Divergenz einer Reihe verwendet.

Teleskopreihen

Die Teleskopreihe $\sum _{n=1}^{\mathrm{\infty }}(b_n-b_{n+1})$ konvergiert genau dann, wenn die Folge $(b_n{)}_{n\in \mathbb{N}}$ gegen eine Zahl $L$ konvergiert. Der Wert der Reihe ist dann $b_1-L$.

Beispiel

Es gilt ${\sum }_{n=1}^{\mathrm{\infty }}\frac{1}{n(n+1)}={\sum }_{n=1}^{\mathrm{\infty }}(\frac{1}{n}-\frac{1}{n+1})=1$, da $a_n=\frac{1}{n}$ gegen $L=0$ konvergiert, und $a_1=1$.

Majorantenkriterium

Vorlage:Hauptartikel Wenn alle Glieder $a_n$ der Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ nichtnegative reelle Zahlen sind, ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ konvergiert und für alle $n$ zudem $a_n\ge |b_n|$ gilt, dann konvergiert auch die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{b}_n$ absolut, und es ist

$\left|\sum _{n=0}^{\mathrm{\infty }}{b}_n\right|\le \sum _{n=0}^{\mathrm{\infty }}{a}_n$.

Beispiel

Es konvergiert für alle $\alpha \in ℝ$ die Reihe ${\sum }_{n=1}^{\mathrm{\infty }}\frac{\sin (\alpha n)}{n^2}$. In der Tat, da $|\sin (\alpha n)|\le 1$, folgt über $\sum _{n=1}^{\mathrm{\infty }}\left|\frac{\sin (\alpha n)}{n^2}\right|\le \sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}<\mathrm{\infty }$ die Behauptung mit dem Majorantenkriterium.

Minorantenkriterium

Wenn alle Glieder $a_n$ der Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ nichtnegative reelle Zahlen sind, ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ divergiert und für alle $n$ zudem $a_n\le b_n$ mit nichtnegativen reellen Zahlen $b_n$ gilt, dann divergiert auch die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{b}_n$.

Beispiel

Es gilt $\frac{1}{\sqrt{n}}\ge \frac{1}{n}\ge 0$ für alle $n\in \mathbb{N}$. Da nun $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}=\mathrm{\infty },$ folgt die Divergenz der Reihe ${\sum }_{n=1}^{\mathrm{\infty }}\frac{1}{\sqrt{n}}$ mit dem Minorantenkriterium.

Quotientenkriterium

Vorlage:Hauptartikel Es wird die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ mit $a_n=0$ für alle bis auf endlich viele $n$ betrachtet (alternativ kann im Voraus die Folge $a_n$ auch unter Weglassen der Nullen auf eine Teilfolge verdichtet werden, die ohne Einschränkung wieder als $a_n$ bezeichnet werden kann). Dann gilt:

• Falls $\underset{n\to \mathrm{\infty }}{\mathrm{lim\; sup}}\left|\frac{a_{n+1}}{a_n}\right|<1$, so ist die Reihe absolut konvergent (dabei steht $\mathrm{lim\; sup}$ für den Limes superior).
• Falls $\underset{n\to \mathrm{\infty }}{\mathrm{lim\; inf}}\left|\frac{a_{n+1}}{a_n}\right|>1$, so ist die Reihe divergent (dabei steht $\mathrm{lim\; inf}$ für den Limes inferior).
• In den verbleibenden Fällen kann keine Aussage getroffen werden, d. h., sowohl bedingte oder absolute Konvergenz, aber auch Divergenz sind möglich.

Die Berechnung der obigen Limites superior und inferior kann schwierig sein, weshalb in vielen Fällen lediglich eine Abschätzung gemacht wird. Ist zum Beispiel $\left|\frac{a_{n+1}}{a_n}\right|\le q<1$ für alle bis auf endlich viele $n$ für eine feste Zahl $q$, so gilt insbesondere $\underset{n\to \mathrm{\infty }}{\mathrm{lim\; sup}}\left|\frac{a_{n+1}}{a_n}\right|\le q<1$, also ist die Reihe absolut konvergent.

Wurzelkriterium

Vorlage:Hauptartikel Zu einer Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ wird die Größe $\alpha :=\underset{n\to \mathrm{\infty }}{\mathrm{lim\; sup}}\sqrt[n]{|a_n|}$ betrachtet (dabei steht $\mathrm{lim\; sup}$ für den Limes superior). Dann gelten folgende Aussagen:

• Ist $\alpha <1$, so konvergiert die Reihe absolut.
• Ist $\alpha >1$, so ist die Reihe divergent.
• Ist $\alpha =1$, so kann keine Aussage getroffen werden, d. h., sowohl bedingte oder absolute Konvergenz, aber auch Divergenz sind möglich.

Im Falle von Potenzreihen dient das Wurzelkriterium beim Beweis der Formel von Cauchy-Hadamard für deren Konvergenzradius.

Die Berechnung des obigen Limes superior kann schwierig sein, weshalb in vielen Fällen lediglich eine Abschätzung gemacht wird. Ist zum Beispiel $\sqrt[n]{|a_n|}\le q<1$ für alle bis auf endlich viele $n$ für eine feste Zahl $q$, so gilt insbesondere $\alpha \le q<1$, also ist die Reihe absolut konvergent.

Kriterium von du Bois-Reymond und Dedekind

Vorlage:Siehe auch Dieses Kriterium kann in zwei Unterkriterien unterteilt werden.

1. Es ist die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n{b}_n$ konvergent, falls ${\sum }_{n=0}^{\mathrm{\infty }}(b_n-b_{n+1})$ absolut und ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ wenigstens bedingt konvergiert.
2. Es ist die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n{b}_n$ konvergent, falls außer der absoluten Konvergenz von ${\sum }_{n=0}^{\mathrm{\infty }}(b_n-b_{n+1})$ lediglich die Beschränktheit der Partialsummen von ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ und $b_n\to 0$ vorausgesetzt wird.

Gaußsches und Weierstraßsches Kriterium

Kann man den Quotienten $\frac{a_{n+1}}{a_n}$ in der Form $1-\frac{\alpha }{n}-\frac{{\vartheta }_n}{n^{\lambda }}$ mit einer beschränkten Folge ${\vartheta }_n$ und $\lambda >1$ schreiben, so ist die Reihe ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ im Falle $\alpha >1$ konvergent, und im Falle $\alpha \le 1$ divergent.

Dieses Kriterium von Gauß kann für komplexe Folgen ausgeweitet werden, wo es als Kriterium von Weierstraß benannt ist. Erfüllen die komplexen Glieder $a_n$

$\frac{a_{n+1}}{a_n}=1-\frac{\alpha }{n}-\frac{A_n}{n^{\lambda }}$

mit $\lambda >1$ und beschränkten $A_n$, so konvergiert die zugehörige Reihe genau dann absolut, wenn $\mathrm{R}\mathrm{e}(\alpha )>1$. Ist $0<\mathrm{R}\mathrm{e}(\alpha )\le 1$, so sind wenigstens die Reihen ${\sum }_{n=1}^{\mathrm{\infty }}|a_n-a_{n+1}|$ und ${\sum }_{n=1}^{\mathrm{\infty }}(-1{)}^n{a}_n$ konvergent.

Kriterien unter Monotoniebedingungen

Monotoniekriterium

Vorlage:Hauptartikel Gilt $a_n\ge 0$ für alle $n\in \mathbb{N}$, so konvergiert ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ genau dann, wenn die Folge $s_N={\sum }_{n=1}^N{a}_n$ beschränkt ist, und der Grenzwert ist $\underset{N\in \mathbb{N}}{\sup }{s}_N$. Ist $a_n$ in diesem Szenario zusätzlich monoton fallend, impliziert die Konvergenz der Reihe auch $n{a}_n\to 0$.

Es ist für beliebige positive $a_n$ die Reihe

$\sum _{n=1}^{\mathrm{\infty }}\frac{a_n}{(1+a_1)(1+a_2)\cdots (1+a_n)}$

konvergent.

Integralkriterium

Vorlage:Hauptartikel Ist $f:[1,\mathrm{\infty })\to [0,\mathrm{\infty })$ eine monoton fallende Funktion mit

$f(n)=a_n$ für alle $n$,

dann konvergiert ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ genau dann, wenn das uneigentliche Integral

$\underset{1}{\overset{\mathrm{\infty }}{\int }}f(x)\mathrm{d}x$

existiert.

Beispiel

Die Dirichletreihe $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^r}$ konvergiert für $r>1$ und divergiert für $r\le 1$, was mit dem Integralkriterium gezeigt werden kann. Als Funktion von $r$ aufgefasst, ergibt diese Reihe die Riemannsche Zeta-Funktion.

Leibniz-Kriterium

Vorlage:Hauptartikel Eine Reihe der Form

$S=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n{a}_n$

mit nichtnegativen $a_n$ wird alternierende Reihe genannt. Eine solche Reihe konvergiert, wenn die Folge $a_n$ monoton gegen 0 konvergiert. Die Umkehrung ist nicht allgemeingültig.

Kriterium von Abel

Vorlage:Hauptartikel Es ist die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n{b}_n$ konvergent, falls die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ konvergiert, und die Folge $b_n$ monoton und beschränkt ist.

Kriterium von Dirichlet

Vorlage:Hauptartikel Es ist die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n{b}_n$ konvergent, falls

$\underset{N\in \mathbb{N}}{\sup }\left|\sum _{n=0}^N{a}_n\right|<\mathrm{\infty },$

also die Partialsummen der $a_n$ beschränkt sind, und wenn $b_n$ eine monoton fallende Nullfolge ist. Dabei steht $\sup$ für das Supremum.

Cauchysches Verdichtungskriterium

Vorlage:Hauptartikel Ist $a_n$ eine monoton fallende Nullfolge, so konvergiert die Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ genau dann, wenn die Reihe ${\sum }_{n=1}^{\mathrm{\infty }}{2}^n{a}_{2^n}$ konvergiert.

Multiplikative Funktionen

Es ist $f:\mathbb{N}\to ℂ$ eine multiplikative Funktion, falls $f(mn)=f(m)f(n)$ für alle teilerfremden $m$ und $n$ gilt.

Es konnte Peter D. T. A. Elliott Folgendes zeigen: Es sei $f$ multiplikativ, sodass

$0=A=\underset{n\to \mathrm{\infty }}{\lim }\frac{1}{n}\sum _{m=1}^{n}f(m)$

existiert, und ferner

$\underset{n\to \mathrm{\infty }}{\mathrm{lim\; sup}}\frac{1}{n}\sum _{m=1}^n|f(m){|}^2<\mathrm{\infty }.$

Dann gilt bereits, dass die Reihen

$\sum _{p\text{Primzahl}}\frac{f(p)-1}{p},\sum _{p\text{Primzahl}}\frac{|f(p)-1{|}^2}{p},\sum _{p\text{Primzahl}}\sum _{k=2}^{\mathrm{\infty }}\frac{|f(p^k)|}{p^k}$

sämtlich konvergieren.

Funktionentheoretische Mittel

Sätze von Tauber und Littlewood

Der Satz von Tauber, bewiesen von Alfred Tauber im Jahr 1897, nutzt das Randverhalten einer Potenzreihe, um ein hinreichendes Kriterium für dortige Konvergenz zu geben. Ist

$f(z)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{z}^n$

für alle $|z|<1$ konvergent, existiert $f(1):=\underset{r\to 1^{-}}{\lim }f(r)$ und gilt $n{a}_n\to 0$ für $n\to \mathrm{\infty }$, so konvergiert ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ gegen $f(1)$. John Edensor Littlewood konnte dieses Resultat verbessern, indem er zeigte, dass bereits die abgeschwächte Bedingung $|n{a}_n|\le C$ für alle $n$ mit einer Konstante $C$ für die Aussage des Satzes hinreichend ist. Diese Bedingung kann im allgemeinen Fall nicht weiter verbessert werden: Zu jeder positiven, wachsenden Funktion $\varphi$ mit $\varphi (n)\to \mathrm{\infty }$ existiert eine Abel-summierbare Folge $a_n$ mit $|a_n|\le \frac{\varphi (n)}{n}$, sodass ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ divergiert. Wird allerdings gefordert, dass die $a_n$ fast alle nichtnegativ sind, kann die Bedingung der Beschränktheit von $n{a}_n$ gänzlich weggelassen werden.

${\sum }_{n=0}^{\mathrm{\infty }}{a}_n=A$ genau dann, wenn $\underset{r\to 1^{-}}{\lim }{\sum }_{n=0}^{\mathrm{\infty }}{a}_n{r}^{2^n}=A$.

Ist stets $n{a}_n\ge -K$ für eine reelle Zahl $K$, dann folgt aus $\underset{\sigma \to 0^{+}}{\lim }{\sum }_{n=0}^{\mathrm{\infty }}{a}_n{e}^{-\sigma n^2}=s$ bereits ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n=s$.

Kriterien von Fatou und Korevaar

Vorlage:Siehe auch Wieder habe $f(z)={\sum }_{n=0}^{\mathrm{\infty }}{a}_n{z}^n$ einen Konvergenzradius von mindestens 1. Gibt es sogar eine Konstante $\alpha >0$, sodass $|f(r)-f(1)|=O((1-r{)}^{\alpha })$ mit $r\to 1^{-}$, so folgt bereits

$|\sum _{k=0}^n{a}_k-f(1)|=O\left(\frac{1}{\log (n)}\right).$

Ist $f$ um $z=1$ holomorph fortsetzbar und gibt es eine nicht-fallende Funktion $\psi :ℝ\to [1,\mathrm{\infty })$, sodass $\psi (x)=1$ für $x\le 0$ und $\psi (2x)\le C\psi (x)$ für $x\ge 0$ mit einer Konstanten $C>0$; gilt zudem $a_n\ge -\frac{1}{\psi (n)}$ für alle $n\ge 0$, dann konvergiert ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ gegen $f(1)$ und zudem gilt

$\sum _{k\le x}{a}_k=f(1)+O\left(\frac{1}{\psi (x)}\right).$

Eine ähnliche Aussage gilt für Dirichlet-Reihen: Ist $F(s):={\sum }_{n=1}^{\mathrm{\infty }}{a}_n{n}^{-s}$ eine Funktion, die für alle $\mathrm{R}\mathrm{e}(s)>1$ konvergiert und sich nach $s=1$ holomorph fortsetzen lässt; gilt ferner $a_n\ge -\frac{1}{\psi (\log (n))}$ für ein $\psi$ wie oben, so gilt bereits

$\sum _{n\le x}\frac{a_n}{n}=F(1)+O\left(\frac{1}{\psi (\log (x))}\right).$

Abel-Summierbarkeit

Vorlage:Siehe auch Man nennt eine formale Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ Abel-summierbar gegen $A$, falls

$\underset{r\to 1^{-}}{\lim }\sum _{n=0}^{\mathrm{\infty }}{a}_n{r}^n=A,$

wobei die Reihe zur Linken für alle $0\le r<1$ konvergiere. Es ist eine Abel-summierbare Reihe genau dann konvergent, wenn

$\underset{n\to \mathrm{\infty }}{\lim }\frac{a_1+2a_2+\cdots +n{a}_n}{n}=0.$

Satz von Fatou

Der Satz Fatou besagt, dass, wenn die Potenzreihe

$f(z)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{z}^n$

für alle $|z|<1$ konvergiert, und sich die Funktion $f$ in einer Umgebung des Randpunkts $|z_0|=1$ holomorph fortsetzen lässt, aus $a_n\to 0$ bereits folgt, dass ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ konvergiert, und den Wert $f(z_0)$ annimmt.

Der Satz von Fatou kann, unter Umgehung der Bedingung der Holomorphie in $z_0$, ausgeweitet werden. Dafür wird das Konzept des Hardy-Raums $H^1(D)$ eines Gebietes $D$ benötigt. Erfüllt $f$ im Randpunkt $z_0=e^{i{t}_0}$ die lokale $H^1$-Bedingung, so existiert eine Zahl $\lambda >0$, sodass $f(r{e}^{it})$ für $r\to 1^{-}$ in $L^1(t_0-\lambda ,t_0+\lambda )$ gegen eine (integrierbare) Funktion $t\mapsto f(e^{it})$ konvergiert (siehe auch Lp-Raum), also

$\underset{r\to 1^{-}}{\lim }\underset{t_0-\lambda }{\overset{t_0+\lambda }{\int }}|f(r{e}^{it})-f(e^{it})|\mathrm{d}t=0.$

Ist die Menge $ℰ$ der Randpunkte $\zeta$, mit $|\zeta |=1$, an der $f$ singulär ist in dem Sinne, dass sie dort nicht die lokale $H^1$-Bedingung erfüllt, eine Nullmenge, und gilt

$\underset{\zeta \in ℰ}{\sup }\underset{n\in {\mathbb{N}}_0}{\sup }\left|\sum _{k=0}^n{a}_k{\zeta }^k\right|=M<\mathrm{\infty },$

dann konvergiert $f$ in jedem Punkt $z_1=e^{i{t}_1}$ gegen $f(z_1)$, an dem der Differenzenquotient

$q_{z_1}(z)=\frac{f(z)-f(z_1)}{z-z_1},|z|<1$

die lokale $H^1$-Bedingung in $z_1$ erfüllt. Dabei steht $\sup$ für das Supremum.

Satz von Ingham

Ein im Jahr 1935 gegebener Satz von Albert Ingham war Ausgangspunkt für weitere Untersuchungen von Donald Newman, der diesen mit einfachen funktionentheoretischen Mitteln beweisen konnte. Sei eine Dirichletreihe

$f(s)=\sum _{n=1}^{\mathrm{\infty }}\frac{a_n}{n^s}$

für alle $s$ mit $\mathrm{R}\mathrm{e}(s)>1$ konvergent (d. h., sie stellt in dieser offenen Halbebene eine holomorphe Funktion dar). Lässt sich $f$ nun holomorph auf eine offene Menge fortsetzen, die $\{s\in ℂ:\mathrm{R}\mathrm{e}(s)\ge 1\}$ vollständig enthält, und sind die $a_n$ beschränkt, so gilt bereits für alle $t\in ℝ$

$\sum _{n=1}^{\mathrm{\infty }}\frac{a_n}{n^{1+it}}=f(1+it).$

Für unbeschränkte $a_n$ ist die obige Aussage bekanntlich falsch.

Methoden zur Grenzwertbestimmung

Es existiert kein allgemein brauchbares Verfahren, den Grenzwert einer konvergenten Reihe explizit auszurechnen. In einigen Fällen lassen sich Grenzwerte auch nicht auf „elementare“ mathematische Konstanten zurückführen, etwa im Fall der Apéry-Konstante

$\zeta (3):=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^3}.$

Allerdings gibt es einige Techniken, die in speziellen Situationen die geschlossene Berechnung eines konvergenten Reihenausdrucks ermöglichen.

Teleskopreihen

Hat eine Reihe die Gestalt ${\sum }_{n=1}^{\mathrm{\infty }}(b_n-b_{n+1})$ mit einer Folge $b_n$, die gegen einen Grenzwert $B$ konvergiert, so konvergiert jene ebenfalls und hat den Grenzwert $b_1-B$. Dieses Resultat lässt sich weiter verallgemeinern. Sind die Glieder der Reihe ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ gegeben durch

$a_n=c_1{x}_n+c_2{x}_{n+1}+\cdots +c_k{x}_{n+k-1}$ mit $k\ge 2$,

wobei $x_n$ gegen den Grenzwert $x$ konvergiert und $c_1+c_2+\cdots +c_k=0$, so konvergiert ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ und der Grenzwert ist explizit gegeben durch

$\sum _{n=1}^{\mathrm{\infty }}{a}_n=c_1{x}_1+(c_1+c_2)x_2+\cdots +(c_1+c_2+\cdots +c_{k-1})x_{k-1}+(c_2+2c_3+\cdots +(k-1)c_k)x$.

Ein Anwendungsbeispiel dieser Regel ist

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{(3n+1)(3n+10)}=\sum _{n=1}^{\mathrm{\infty }}(\frac{1}{9(3n+1)}-\frac{1}{9(3n+10)})=\frac{1}{9}\cdot \frac{1}{4}+\frac{1}{9}\cdot \frac{1}{7}+\frac{1}{9}\cdot \frac{1}{10}+3\cdot (-\frac{1}{9})\cdot 0=\frac{23}{420}.$

Abelscher Grenzwertsatz

Es sei ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ eine konvergente Reihe. Eine Möglichkeit, ihren Grenzwert zu bestimmen, geht über die von den $a_n$ erzeugte Funktion. Niels Henrik Abel konnte beweisen, dass sich die Funktion

$f(x):=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n$

stetig nach $x=1$ fortsetzen lässt. Ferner gilt

$f(1)=\sum _{n=0}^{\mathrm{\infty }}{a}_n.$

In einem rechtwinkligen, gleich­schenkligen Dreieck mit $45$°-Winkeln (entspricht $\frac{\pi }{4}$ im Bogenmaß) berechnet sich der Tangens von $\frac{\pi }{4}$ durch das Verhältnis beider (gleichlanger) Katheten, ist also gerade $1$. Entsprechend nimmt seine Umkehrfunktion, der Arkustangens, an der Stelle $1$ den Wert $\frac{\pi }{4}$ an.

Mit diesem Ansatz können manche klassischen Reihengrenzwerte berechnet werden. Beispielsweise gilt für alle $x$ mit $|x|<1$ gilt die Reihendarstellung

$\arctan (x)=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n+1}}{2n+1}.$

Mit dem Leibniz-Kriterium und der Abel-Summierbarkeit folgt damit die Leibniz-Reihe:

$\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots =\arctan (1)=\frac{\pi }{4}.$

Ähnlich verhält es sich mit der Taylorreihe des natürlichen Logarithmus:

$\log (1+x)=\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{n+1}}{n+1}.$

Damit folgt, dass die alternierende harmonische Reihe den Grenzwert $\log (2)$ besitzt:

$\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n-1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots =\log (2).$

Beide Reihen zeigen zwar ein klares „Bildungsgesetz“, sind jedoch für numerische Berechnungen unbrauchbar.

Differential- und Integralrechnung

Ansätze über Differential- und Integralrechnung greifen primär auf Eigenschaften von Potenzreihen zurück. In manchen Fällen kann der Grenzwert einer Reihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n$ ermittelt werden, indem man die allgemeinere Potenzreihe ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n{x}^n$ für Werte $|x|\le 1$ studiert. Im einfachsten Fall gilt:

• Die Reihe $f(x)={\sum }_{n=0}^{\mathrm{\infty }}{a}_n{x}^n$ hat Konvergenzradius $R>1$,
• und es lässt sich $f(x)$ durch bekannte Funktionen geschlossen ausdrücken.

Dann kann mit

$f(1)=\sum _{n=0}^{\mathrm{\infty }}{a}_n$

direkt ein geschlossener Grenzwert hingeschrieben werden, und Konvergenz folgt ebenso automatisch. Ist der Konvergenzradius jedoch genau $R=1$, muss im Rahmen des Abelschen Grenzwertsatzes zunächst Konvergenz nachgewiesen werden (siehe oben).

Dieser Ansatz kann schnell auf Reihen des Typs

$\sum _{n=0}^{\mathrm{\infty }}{n}^k{a}_n$

mit $k\in {\mathbb{N}}_0$ verallgemeinert werden. In der obigen Situation mit Konvergenzradius $R>1$ sind diese sämtlich absolut konvergent, und Grenzwerte können geschlossen über die höheren Ableitungen der Funktion $f$ an der Stelle $x=1$ ausgedrückt werden. Zum Beispiel gilt mit obiger Notation

$\sum _{n=0}^{\mathrm{\infty }}n{a}_n=f^{\prime }(1),$

$\sum _{n=0}^{\mathrm{\infty }}{n}^2{a}_n=f^{″}(1)+f^{\prime }(1),$

$\sum _{n=0}^{\mathrm{\infty }}{n}^3{a}_n=f^{‴}(1)+3f^{″}(1)+f^{\prime }(1)$

und ganz allgemein

$\sum _{n=0}^{\mathrm{\infty }}{n}^k{a}_n=\sum _{\ell =1}^k\left\{\genfrac{}{}{0ex}{}{k}{\ell }\right\}{f}^{(\ell )}(1),$ (für $k\in \mathbb{N}$),

wobei $\left\{\genfrac{}{}{0ex}{}{k}{\ell }\right\}$ die Stirling-Zahlen zweiter Art sind. Ein einfaches Beispiel betrifft die Reihe

$\sum _{n=0}^{\mathrm{\infty }}\frac{n}{2^n}=\frac{0}{1}+\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+\frac{4}{16}+\cdots .$

Es gilt mit der geometrischen Reihe $f(x)={\sum }_{n=0}^{\mathrm{\infty }}\frac{x^n}{2^n}=\frac{1}{1-\frac{x}{2}}$ für alle $|x|<2$ (weshalb die betrachtete Reihe definitiv absolut konvergiert), und mit $f^{\prime }(x)=\frac{1}{2(1-\frac{x}{2}{)}^2}$ der Grenzwert ${\sum }_{n=0}^{\mathrm{\infty }}\frac{n}{2^n}=f^{\prime }(1)=2$.

Mitunter noch einfacher gestaltet sich dieser Ansatz beim Übergang zu Fourierreihen durch den Variablenwechsel $x=e^{it}$. Man betrachtet dann

$\varphi (t)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{e}^{itn}$

im Punkt $t=0$ und beim Ableiten dieser Reihe sind keine Stirling-Zahlen mehr vonnöten (allerdings wird gleichzeitig wegen Verkettung das Aufstellen geschlossener Ableitungsterme meist schwieriger). Im Rahmen der charakteristischen Funktion ist dieses Vorgehen in der Wahrscheinlichkeitstheorie bei der Berechnung von Momenten diskreter Zufallsvariablen nützlich, siehe auch momenterzeugende Funktion.

In einigen Fällen können Reihen direkt auf gewisse Integrale zurückgeführt werden, wobei Letztere dann mit Methoden der Analysis, zum Beispiel durch Auswertung mit Angabe einer Stammfunktion, gelegentlich geschlossen berechnet werden können. Die Umwandlung von Integral in Reihe ergibt sich dabei im Falle von Funktionenreihen oft durch gliedweise Integration. Ein Beispiel ist die Leibniz-Reihe:

$\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{2n+1}=\sum _{n=0}^{\mathrm{\infty }}\underset{0}{\overset{1}{\int }}(-1{)}^n{x}^{2n}\mathrm{d}x=\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}x}{x^2+1}=\arctan (1)-\arctan (0)=\frac{\pi }{4}.$

David Bailey, Peter Borwein und Simon Plouffe benutzten die Integralformel

$\pi =\underset{0}{\overset{\frac{1}{\sqrt{2}}}{\int }}\frac{4\sqrt{2}-8x^3-4\sqrt{2}{x}^4-8x^5}{1-x^8}\mathrm{d}x=\underset{0}{\overset{1}{\int }}\frac{16y-16}{y^4-2y^3+4y-4}\mathrm{d}y=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{16^n}(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6})$

beim Beweis der Bailey-Borwein-Plouffe-Formel für die Kreiszahl $\pi$. Ein anderes Beispiel betrifft eine Lösung des Basler Problems über den Ansatz

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}=\frac{4}{3}\underset{0}{\overset{1}{\int }}\frac{\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(x)}{x}\mathrm{d}x=\frac{{\pi }^2}{6}$,

wobei $\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}$ den Areatangens Hyperbolicus bezeichnet.

Fourieranalysis

Die Grenzwertbestimmung über Fourierreihen ähnelt dem Grenzwertsatz von Abel insofern, als dass die Reihe auch hier als Wert einer zu bestimmenden Funktion interpretiert wird. Weiß man, dass ${\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_n$ absolut konvergiert, so kann man diesen Wert als $f(0)$ mit

$f(x):=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_n{e}^{2\pi ixn}$

auffassen. Dann ist $f$ eine 1-periodische Funktion und die rechte Seite ihre Darstellung als Fourierreihe. Über die Umrechnungsformel

$a_n=\underset{0}{\overset{1}{\int }}f(x)e^{-2\pi inx}\mathrm{d}x$

können die Koeffizienten der Reihe aus $f$ zurückgewonnen werden. Es muss also ein „passendes“ $f$ zu den $a_n$ gefunden werden. Zum Beispiel findet man mit partieller Integration schnell

$\frac{(\pi -x{)}^2}{4}=\frac{{\pi }^2}{12}+\sum _{n=1}^{\mathrm{\infty }}\frac{\cos (xn)}{n^2},(0\le x\le 2\pi ),$

womit durch Einsetzen von $x=0$ die Antwort auf das Basler Problem folgt. Ist $f$ lediglich als auf dem Intervall $[0,1]$ integrierbar vorausgesetzt, und hat die assoziierte Fourierreihe ${\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_n{e}^{2\pi ixn}$, so gilt außerdem die Parsevalsche Identität

$\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}|a_n{|}^2=\underset{0}{\overset{1}{\int }}|f(x){|}^2\mathrm{d}x.$

Residuensatz

In manchen Fällen, besonders bei unendlichen Reihen über rationale Funktionen, kann der Residuensatz aus der Funktionentheorie verwendet werden. Ist $f:ℂ\to \overline{ℂ}$ eine meromorphe Funktion mit endlichen vielen, nicht ganzzahligen Polstellen $z_1,\dots ,z_n$, so gilt, falls zusätzlich $f(z)=O(|z{|}^{-\nu })$ mit $|z|\to \mathrm{\infty }$ und $\nu >1$, die Formel

$\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}f(k)=-\sum _{j=1}^n{\mathrm{R}\mathrm{e}\mathrm{s}}_{z=z_j}(\pi \cot (\pi z)f(z)).$

Ähnlich gilt

$\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}(-1{)}^{k}f(k)=-\sum _{j=1}^n{\mathrm{R}\mathrm{e}\mathrm{s}}_{z=z_j}(\pi \csc (\pi z)f(z)).$

Dabei bezeichnet $\cot$ den Kotangens und $\csc$ den Kosekans. Diese Aussage beinhaltet folgenden Spezialfall: Sind $P(z)$ und $Q(z)$ Polynome, sodass $\mathrm{deg}(Q)\ge \mathrm{deg}(P)+2$ und $Q(k)=0$ für alle $k\in \mathbb{Z}$, so folgt

$\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{P(k)}{Q(k)}=-\sum _{Q(w)=0}{\mathrm{R}\mathrm{e}\mathrm{s}}_{z=w}\left(\frac{\pi \cot (\pi w)P(z)}{Q(z)}\right).$

Mit diesem Verfahren lässt sich zum Beispiel ${\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{k^2+1}=\pi \coth (\pi )=\pi \frac{e^{2\pi }+1}{e^{2\pi }-1}$ und ${\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{(-1{)}^k}{k^2+1}=\pi \mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}(\pi )=\pi \frac{2e^{\pi }}{e^{2\pi }-1}$ zeigen.

Ist $f$ eine ganze Funktion, sodass es eine Folge $0<R_n\to \mathrm{\infty }$ gibt, sodass

$\underset{n\to \mathrm{\infty }}{\lim }{\oint }_{|z|=R_n}\frac{f(z)}{z\cos \left(\frac{\pi z}{2}\right)}\mathrm{d}z=0$,

dann gilt

$\underset{N\to \mathrm{\infty }}{\lim }\sum _{k=-N}^N\frac{(-1{)}^{k}f(2k+1)}{2k+1}=\frac{\pi }{2}f(0).$

Wird $\cos (\frac{\pi z}{2})$ durch $\sin (\pi z)$ ersetzt, gilt unter sonst gleichen Bedingungen

$\underset{N\to \mathrm{\infty }}{\lim }\sum _{\genfrac{}{}{0ex}{}{k=-N}{k=0}}^N\frac{(-1{)}^{k-1}f(k)}{k}=f^{\prime }(0).$

Ungleichungen

Ungleichungen für Reihen verwenden oft spezielle analytische Methoden, etwa aus der Fourier-Analysis.

Dreiecksungleichungen

Es gilt stets für reelle oder auch komplexe $z_n$

$\left|\sum _{n=1}^{\mathrm{\infty }}{z}_n\right|\le \sum _{n=1}^{\mathrm{\infty }}|z_n|.$

Dies ist die Dreiecksungleichung für Reihen. Sind die Zahlen $z_n$ reell, gilt Gleichheit genau dann, wenn sämtliche $z_n$ nicht-negativ oder nicht-positiv sind. Für allgemeine komplexe Zahlen gilt Gleichheit genau dann, wenn alle $z_n$ auf einer gleichen, bei $0$ startenden, Halbgeraden in der komplexen Ebene liegen (mit anderen Worten, dass alle $z_n=0$ dasselbe komplexe Argument haben). Dies ergibt sich mit $\cos (0)=1$ aus der umgekehrten Dreiecksungleichung, siehe unten.

Allgemeiner gilt für Multireihen

$|\sum _{n_1=1}^{\mathrm{\infty }}\sum _{n_2=1}^{\mathrm{\infty }}\cdots \sum _{n_{\ell }=1}^{\mathrm{\infty }}{z}_{n_1,n_2,\dots ,n_{\ell }}|\le \sum _{n_1=1}^{\mathrm{\infty }}|\sum _{n_2=1}^{\mathrm{\infty }}\cdots \sum _{n_{\ell }=1}^{\mathrm{\infty }}{z}_{n_1,n_2,\dots ,n_{\ell }}|\le \sum _{n_1=1}^{\mathrm{\infty }}\sum _{n_2=1}^{\mathrm{\infty }}|\sum _{n_3=1}^{\mathrm{\infty }}\cdots \sum _{n_{\ell }=1}^{\mathrm{\infty }}{z}_{n_1,n_2,\dots ,n_{\ell }}|\le \cdots \le \sum _{n_1=1}^{\mathrm{\infty }}\sum _{n_2=1}^{\mathrm{\infty }}\cdots \sum _{n_{\ell }=1}^{\mathrm{\infty }}\left|z_{n_1,n_2,\dots ,n_{\ell }}\right|.$

Im Laufe der Zeit wurden zahlreiche Varianten solcher „Dreiecksungleichungen“ gefunden. Sind zum Beispiel $a_1,\dots ,a_n$ positive Zahlen mit ${\sum }_{j=1}^n\frac{1}{a_j}=1$, so gilt stets

${\left|\sum _{j=1}^n{z}_j\right|}^2\le \sum _{j=1}^n{a}_j|z_j{|}^2.$

Allgemeiner gilt für irgendwelche positiven Zahlen $p_1,\dots ,p_n$ und $r>1$ sogar stets

${\left|\sum _{j=1}^n{z}_j\right|}^r\le {\left(\sum _{j=1}^n{p}_j^{\frac{1}{1-r}}\right)}^{r-1}(\sum _{j=1}^n{p}_j|z_j{|}^r).$

Auch umgekehrte Dreiecksungleichungen wurden gefunden. Ist $0\le \theta <\frac{\pi }{2}$ und $a$ eine reelle Zahl, sodass für komplexen Zahlen $z_1,\dots ,z_n$ stets ein $a-\theta \le {\alpha }_j\le a+\theta$ und $r_j\ge 0$ existiert mit $z_j=r_j{e}^{i{\alpha }_j}$, so gilt

$\sum _{j=1}^n|z_j|\le \frac{1}{\cos (\theta )}\left|\sum _{j=1}^n{z}_j\right|.$

Diese Ungleichung verallgemeinert das Kriterium absoluter Konvergenz auf komplexe Zahlen: Liegen alle Summanden $z_j$ einer Reihe in einem gemeinsamen Winkelbereich, dessen Aufspannung weniger als $\pi$ (also 180 Grad) entspricht, konvergiert ${\sum }_{j=1}^{\mathrm{\infty }}{z}_j$ genau dann absolut, wenn die Folge der Absolutwerte der Partialsummen $\left|{\sum }_{j=1}^n{z}_j\right|$ beschränkt ist. Zu beachten ist jedoch, dass dieses Kriterium und auch eine Ungleichung oberen Typs für den Fall reeller $z_j$ mit gemischten Vorzeichen im Allgemeinen nicht existiert, da $\cos (\frac{\pi }{2})=0$, weshalb hier je nach Einzelfall andere Methoden zur Abschätzung gefunden werden müssen. Aus unter anderem diesem Grund sind Reihen mit reellen Gliedern gemischten Vorzeichens nicht nur besonders interessant, sondern gleichzeitig auch besonders schwierig.

Sind allgemein $z_1,\dots ,z_m$ komplexe Zahlen, so existiert stets eine (von diesen Zahlen abhängige) Teilmenge $I\subset \{1,\dots ,m\}$, sodass

$\sum _{j=1}^m|z_j|\le \pi \left|\sum _{j\in I}{z}_j\right|.$

Dabei bezeichnet $\pi$ die Kreiszahl.

Vergleich zum geometrischen Mittel

Für nicht-negative Zahlen $a_1,a_2,\dots ,a_n$ gilt

$n\cdot \sqrt[n]{a_1{a}_2\cdots a_n}\le \sum _{k=1}^n{a}_k.$

Diese Ungleichung ist scharf in dem Sinne, dass Gleichheit genau dann gilt, falls $a_1=a_2=\cdots =a_n$. In allen anderen Fällen ist die linke Seite echt kleiner als die rechte. Diese Ungleichung vergleicht arithmetisches und geometrisches Mittel.

Integralvergleich

Ist $f:[1,\mathrm{\infty })\to {ℝ}_{\ge 0}$ monoton fallend, so gilt

$\sum _{n=2}^{N}f(n)\le \underset{1}{\overset{N}{\int }}f(x)\mathrm{d}x\le \sum _{n=1}^{N-1}f(n).$

Daraus folgt direkt das Integralkriterium, also dass unter obigen Voraussetzungen die Reihe ${\sum }_{n=1}^{\mathrm{\infty }}f(n)$ genau dann konvergiert, falls ${\int }_1^{\mathrm{\infty }}f(x)\mathrm{d}x$ existiert.

Fehler- und Restgliedabschätzung

Alternierende Reihen

Ist $a_n$ eine monoton fallende Nullfolge, so konvergiert ${\sum }_{n=1}^{\mathrm{\infty }}(-1{)}^{n-1}{a}_n$ nach dem Leibnizkriterium gegen einen Grenzwert $S$ und es gilt

$|S-\sum _{n=1}^N(-1{)}^{n-1}{a}_n|\le a_{N+1}.$

Ferner gilt stets $|S|\le a_1$. Dies kann weitreichend verallgemeinert werden: Es gilt unter oberen Voraussetzungen

$|\sum _{n=m}^M(-1{)}^{n-1}{a}_n|\le a_m$

für alle $M\ge m\ge 1$.

Abelsche Ungleichung

Sei $a_n$ eine monoton fallende Nullfolge und $b_n$ eine Folge mit beschränkten Partialsummen, also

$\underset{N\in \mathbb{N}}{\sup }\left|\sum _{n=1}^N{b}_n\right|=:B<\mathrm{\infty }$

Dann konvergiert ${\sum }_{k=1}^{\mathrm{\infty }}{a}_k{b}_k$ und es gilt für alle $m\in \mathbb{N}$ die Ungleichung

$\left|\sum _{k=m}^{\mathrm{\infty }}{a}_k{b}_k\right|\le 2B{a}_m$.

Taylorreihen

Es können auch Restglieder in Taylorreihen abgeschätzt werden. Ist $f$ innerhalb einer offenen Menge der komplexen Zahlen, die die Kreisscheibe $\overline{B_R(0)}$ enthält, holomorph bzw. analytisch, so gilt für alle $|z|<R$

$f(z)=\sum _{k=0}^{N-1}\frac{f^{(k)}(0)}{k!}{z}^k+\frac{z^N}{2\pi i}{\oint }_{\partial B_R(0)}\frac{f(w)}{w^N(w-z)}\mathrm{d}w.$

Damit folgt für $|z|<R$ die Restgliedabschätzung

$\left|\sum _{k=N}^{\mathrm{\infty }}\frac{f^{(k)}(0)}{k!}{z}^k\right|\le \frac{|z{|}^N}{2\pi }{\oint }_{\partial B_R(0)}\left|\frac{f(w)}{w^N(w-z)}\mathrm{d}w\right|\le R{\left(\frac{|z|}{R}\right)}^N\underset{|w|=R}{\max }\left|\frac{f(w)}{w-z}\right|$.

Ist insbesondere $z$ hinreichend klein, etwa $|z|<\frac{R}{2}$, so kann dies vereinfacht durch

$\left|\sum _{k=N}^{\mathrm{\infty }}\frac{f^{(k)}(0)}{k!}{z}^k\right|{\ll }_{R,N}{z}^N\underset{|w|=R}{\max }|f(w)|$

ausgedrückt werden, wobei die implizite Konstante von $R$ und $N$, aber nicht von $z$ und $f$ abhängt.

Symmetrische Ungleichungen

Eine Funktion $f:I\to {ℝ}^{+}$ auf einem Intervall $I$ gehört der Klasse $Q(I)$ an, falls für alle $0<\lambda <1$ sowie $x,y\in I$ die Ungleichung

$f(\lambda x+(1-\lambda )y)\le \frac{f(x)}{\lambda }+\frac{f(y)}{1-\lambda }$

erfüllt ist. Unter diesen Voraussetzungen gilt für $[m,M]\subset I$, $(x_1,\dots ,x_n)\in [m,M{]}^n$, und beliebige positive $p_1,\dots ,p_n$ die Ungleichung

$\sum _{j=1}^n\frac{f(x_j)}{p_j}\le f(m)\sum _{j=1}^n\frac{M-m}{p_j(M-x_j)}+f(M)\sum _{j=1}^n\frac{M-m}{p_j(x_j-m)}.$

Eine direkte Folgerung ist im Falle von $m=0=f(0)$ sowie $M:={\sum }_{j=1}^n{x}_j$:

$\sum _{j=1}^{n}f(x_j)\le f\left(\sum _{j=1}^n{x}_j\right)\left(\sum _{j=1}^n{x}_j\right)\left(\sum _{j=1}^n\frac{1}{x_j}\right).$

Besselsche Ungleichung und die Halasz-Montgomery-Ungleichungen

Es sei $V$ ein $ℂ$-Vektorraum mit Skalarprodukt $⟨,⟩$. Ist $(e_j{)}_{j\in J}$ ein orthonormales System von $|J|$ Vektoren aus $V$, so gilt

$\sum _{j\in J}|⟨e_j,v⟩{|}^2\le ⟨v,v⟩.$

Dies ist die sog. Besselsche Ungleichung. Diese lässt sich auf die Halasz-Montgomery-Ungleichungen verallgemeinern. Sind $(w_j{)}_{j\in J}$ dieses Mal irgendwelche Elemente aus $V$, so gelten

$\sum _{j\in J}|⟨w_j,v⟩|\le {(⟨v,v⟩\sum _{r,s\in J}|⟨w_r,w_s⟩|)}^{\frac{1}{2}}$

$\sum _{j\in J}|⟨w_j,v⟩{|}^2\le ⟨v,v⟩\underset{j\in J}{\sup }\sum _{s\in J}|⟨w_j,w_s⟩|.$

Hausdorff-Young-Ungleichung

Sei $f:ℝ\to ℂ$ 1-periodisch, auf $[0,1]$ integrierbar mit assoziierter Fourierreihe ${\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}{a}_n{e}^{2\pi ixn}$. Sind $1\le p\le 2$ und $2\le q\le \mathrm{\infty }$ so gewählt, dass $\frac{1}{p}+\frac{1}{q}=1$, so gilt die Hausdorff-Young-Ungleichung

${(\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}|a_n{|}^q)}^{\frac{1}{q}}\le {(\underset{0}{\overset{1}{\int }}|f(x){|}^p\mathrm{d}x)}^{\frac{1}{p}}$

und ihre „Duale“

${(\underset{0}{\overset{1}{\int }}|f(x){|}^q\mathrm{d}x)}^{\frac{1}{q}}\le {(\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}|a_n{|}^p)}^{\frac{1}{p}}$.

Cauchy-Schwarzsche Ungleichung und Höldersche Ungleichung

Für beliebige komplexe Zahlen $a_j,b_j\in ℂ$ gilt die folgende Ungleichung für Partialsummen

$\sum _{j=1}^n|a_j{b}_j|\le {(\sum _{j=1}^n|a_j{|}^2)}^{\frac{1}{2}}{(\sum _{j=1}^n|b_j{|}^2)}^{\frac{1}{2}}.$

Diese wird als Cauchy-Schwarzsche Ungleichung bezeichnet. Konvergieren beide Reihen für $n\to \mathrm{\infty }$ zur Rechten, kann auch auf die Konvergenz der linken Seite geschlossen werden, und es gilt die entsprechende Ungleichung für die Grenzwerte. Eine unter Zusatzbedingungen verbesserte Version stammt von Nicolaas Govert de Bruijn: Sind $a_1,\dots ,a_n$ reell und $z_1,\dots ,z_n$ komplex, dann gilt

${\left|\sum _{j=1}^n{a}_j{z}_j\right|}^2\le \frac{1}{2}(\sum _{j=1}^n|z_j{|}^2+\left|\sum _{j=1}^n{z}_j^2\right|)\left(\sum _{j=1}^n{a}_j^2\right)$.

Hat man allgemein $1<p,q<\mathrm{\infty }$ mit $\frac{1}{p}+\frac{1}{q}=1$, so gilt allgemeiner die Höldersche Ungleichung

$\sum _{j=1}^n|a_j{b}_j|\le {(\sum _{j=1}^n|a_j{|}^p)}^{\frac{1}{p}}{(\sum _{j=1}^n|b_j{|}^q)}^{\frac{1}{q}}.$

Es kann aus der Konvergenz des rechten Ausdrucks auf die Konvergenz der linken Reihe rückgeschlossen werden. Im Grenzfall $q=\mathrm{\infty }$ entspricht dies

$\sum _{j=1}^{\mathrm{\infty }}|a_j{b}_j|\le (\sum _{j=1}^{\mathrm{\infty }}|a_j|)\cdot \underset{j\in \mathbb{N}}{\sup }|b_j|$.

Die Hölder-Ungleichung lässt sich gewichten. Für positive $w_1,\dots ,w_n$ gilt

$\sum _{j=1}^n{w}_j|a_j{b}_j|\le {(\sum _{j=1}^n{w}_j|a_j{|}^p)}^{\frac{1}{p}}{(\sum _{j=1}^n{w}_j|b_j{|}^q)}^{\frac{1}{q}}.$

Minkowski-Ungleichung

Wenn $p\ge 1$ ist und $a_j$ und $b_j$ beliebige komplexe Zahlen sind, so gilt bereits die Minkowski-Ungleichung

${(\sum _{j=1}^{\mathrm{\infty }}|a_j+b_j{|}^p)}^{\frac{1}{p}}\le {(\sum _{j=1}^{\mathrm{\infty }}|a_j{|}^p)}^{\frac{1}{p}}+{(\sum _{j=1}^{\mathrm{\infty }}|b_j{|}^p)}^{\frac{1}{p}}.$

Die Minkowski-Ungleichung lässt sich verallgemeinern: Ist $f:[0,\mathrm{\infty })\to ℝ$ stetig, streng monoton steigend und konvex mit $f(0)=0$ sowie $F(x):=\log (f(e^x))$ konvex für alle $x\in ℝ$, so gilt für alle nicht-negativen $a_1,\dots ,a_n$ und $b_1,\dots ,b_n$

$f^{-1}(\sum _{j=1}^{n}f(a_j+b_j))\le f^{-1}(\sum _{j=1}^{n}f(a_j))+f^{-1}(\sum _{j=1}^{n}f(b_j)).$

Dabei ist $f^{-1}$ die Umkehrfunktion von $f$.

Gutzmersche Ungleichung

Ist $f$ eine in einer Umgebung $U$ von $0$ holomorphe Funktion mit Potenzreihe $f(z)={\sum }_{n=0}^{\mathrm{\infty }}{a}_n{z}^n$ mit dem Konvergenzradius $r>0$, dann gilt für jedes $0<\varrho <r$ mit $B_{\varrho }(0)\subset U$ die Ungleichung

$\sum _{n=0}^{\mathrm{\infty }}|a_n{|}^2{\varrho }^{2n}\le {(\underset{|z|=\varrho }{\max }|f(z)|)}^2.$

Die Ungleichung geht auf August Gutzmer aus dem Jahr 1888 zurück.

Hilbert-Ungleichung

Ist $f(z)={\sum }_{n=0}^{\mathrm{\infty }}{a}_n{z}^n$ auf der abgeschlossenen Einheitskreis­scheibe $\{z\in ℂ:|z|\le 1\}$ holomorph, so gilt bereits die Hilbert-Ungleichung

$\sum _{m=0}^{\mathrm{\infty }}\sum _{n=0}^{\mathrm{\infty }}\frac{|a_m{a}_n|}{m+n+1}\le \pi \sum _{n=0}^{\mathrm{\infty }}|a_n{|}^2<\mathrm{\infty }.$

Der Faktor $\pi$ ist dabei optimal. Dies kann auf allgemeinere diskrete Mengen ausgeweitet werden. Sind ${\lambda }_1<{\lambda }_2<\cdots <{\lambda }_R$ und

$\delta :=\underset{s=r}{\min }|{\lambda }_r-{\lambda }_s|,{\delta }_r:=\underset{s:s=r}{\min }|{\lambda }_r-{\lambda }_s|,$

dann gelten

$\left|\sum _{\genfrac{}{}{0ex}{}{1\le r,s\le R}{r=s}}\frac{u_r\overline{u_s}}{{\lambda }_r-{\lambda }_s}\right|\le \pi {\delta }^{-1}\sum _{r=1}^R|u_r{|}^2,$

$\left|\sum _{\genfrac{}{}{0ex}{}{1\le r,s\le R}{r=s}}\frac{u_r\overline{u_s}}{{\lambda }_r-{\lambda }_s}\right|\le \sqrt{22}\sum _{r=1}^R|u_r{|}^2{\delta }_r^{-1}.$

Eine weitere Variante der Hilbert-Ungleichung betrifft stetige Funktionen $f:[0,1]\to ℝ$. Es gilt

$\sum _{n=0}^{\mathrm{\infty }}{(\underset{0}{\overset{1}{\int }}{x}^{n}f(x)\mathrm{d}x)}^2\le \pi \underset{0}{\overset{1}{\int }}f(x{)}^2\mathrm{d}x.$

Eine andere Variante betrifft bestimmte Exponentialreihen. Für komplexe $a_n$ und reelle Zahlen $1\le t_1<t_2<\cdots <t_R\le T$ mit $t_r+1\le t_{r+1}$ für alle $1\le r<R$ gilt

$\sum _{r=1}^R{\left|\sum _{n=1}^N{a}_n{n}^{i{t}_r}\right|}^2\le 2\log (N)(T\sum _{n=1}^N|a_n{|}^2+16\sum _{n=1}^{N}n|a_n{|}^2).$

Van der Corputsche Ungleichung

Diese ist eine Anwendung der Cauchy-Schwarzschen Ungleichung. Für komplexe Zahlen $a_n$ sowie natürliche Zahlen $N,H$ gilt

${\left|\sum _{n=1}^N{a}_n\right|}^2\le \frac{N+H}{H+1}\sum _{n=1}^N|a_n{|}^2+\frac{2(N+H)}{H+1}\sum _{h=1}^H(1-\frac{h}{H+1})\left|\sum _{n=1}^{N-h}{a}_{n+h}\overline{a_n}\right|.$

Dabei bezeichnet $\bar{z}$ die komplexe Konjugation der Zahl $z$.

Diese Aussage kann weiter verallgemeinert werden. Sei $T$ ein Fourier-Polynom

$T(x):=\sum _{h=0}^H{b}_h\cos (2\pi hx)$

mit $T(0)=1$ und $T(x)\ge 0$ für alle $x\in ℝ$. Dann gilt

${\left|\sum _{n=1}^N{a}_n\right|}^2\le (N+H)(b_0\sum _{n=1}^N|a_n{|}^2+\sum _{h=1}^H\left|b_h\sum _{n=1}^{N-h}{a}_{n+h}\overline{a_n}\right|).$

Exponentialsummen

Kusmin-Landau-Ungleichung

Es sei $f:\mathbb{Z}\to ℝ$, sodass $\mathrm{\Delta }f(n):=f(n+1)-f(n)$ monoton für $a+1\le n\le b-1$ für gewählte ganzzahlige $a<b$. Es gebe nun $N\in \mathbb{Z}$ und $0<\vartheta ,\phi <1,$ sodass

$N+\vartheta \le \mathrm{\Delta }f(n)\le N+1-\phi$

für alle $a+1\le n\le b-1$. Dann gilt

$\left|\sum _{a<n\le b}{e}^{2\pi if(n)}\right|\le \frac{1}{2}(\cot \left(\frac{\pi \vartheta }{2}\right)+\cot \left(\frac{\pi \phi }{2}\right)).$

In einer Variante bleibt die Gültigkeit dieser Ungleichung bestehen, wenn $f:[a,b]\to ℝ$ stetig differenzierbar ist mit monotoner Ableitungsfunktion $f^{\prime }$, sodass $N+\vartheta \le f^{\prime }(t)\le N+1-\phi$.

Der Satz von van der Corput

Sei $f:\mathbb{Z}\to ℝ$, und seien ganze $a,b$ mit $b\ge a+3\ge 3$ gewählt. Es sei ${\mathrm{\Delta }}^{2}f(n):=f(n+2)-2f(n+1)+f(n)$ stets positiv oder stets negativ. Ist $|{\mathrm{\Delta }}^{2}f(n)|\ge \lambda >0$, so ist

$\left|\sum _{a<n\le b}{e}^{2\pi if(n)}\right|\le \frac{5|f(b)-f(b-1)-f(a+2)+f(a+1)|+11}{\sqrt{\lambda }}.$

Ist überdies $|{\mathrm{\Delta }}^{2}f(n)|\le c\lambda$ mit einem $c\ge 1$, so gilt

$\left|\sum _{a<n\le b}{e}^{2\pi if(n)}\right|\le 5c(a-b)\sqrt{\lambda }+\frac{11}{\sqrt{\lambda }}.$

Sowohl die Kusmin-Landau-Ungleichung als auch der Satz von van der Corput besitzen höherdimensionale Verallgemeinerungen.

Weyl-Ungleichung

Ist $P$ ein reelles Polynom mit Grad $k$, dessen Leitkoeffizient $\alpha$ eine Approximation

$|\alpha -\frac{a}{q}|\le \frac{c}{q^2}$

mit $q\ge 1$ und $\mathrm{g}\mathrm{g}\mathrm{T}(a,q)=1$ sowie einem fixierten $c>0$ hat, so gibt es für jedes $\epsilon >0$ eine Konstante $C(c,\epsilon )>0$ mit

$\left|\sum _{m=1}^N{e}^{2\pi iP(m)}\right|\le C(c,\epsilon )N^{1+\epsilon }{(\frac{1}{N}+\frac{1}{q}+\frac{q}{N^k})}^{\frac{1}{2^{k-1}}}.$

Das große Sieb

Es seien $a_n$ komplexe Zahlen, $M\in \mathbb{Z},N\in \mathbb{N}$ und $\alpha$ eine reelle Zahl. Definiere die Exponentialsumme

$S(\alpha ):=\sum _{M<n\le M+N}{a}_n{e}^{2\pi in\alpha }.$

Dann gilt für jedes $\delta >0$ die Abschätzung

$|S(\alpha ){|}^2\le \frac{1}{\delta }\underset{\alpha -\frac{\delta }{2}}{\overset{\alpha +\frac{\delta }{2}}{\int }}|S(\beta ){|}^2\mathrm{d}\beta +\underset{\alpha -\frac{\delta }{2}}{\overset{\alpha +\frac{\delta }{2}}{\int }}|S(\beta )S^{\prime }(\beta )|\mathrm{d}\beta .$

Mit Hilfe dieser Integralungleichung können weitere Ungleichungen des folgenden Typs erhalten werden. Ist $({\alpha }_r{)}_{1\le r\le R}$ eine Familie reeller Zahlen

$\delta =\underset{i=j}{\min }||{\alpha }_i-{\alpha }_j||$

wobei $0\le ||x||<1$ das eindeutige Element von $x+\mathbb{Z}$ in $[0,1)$ ist, gilt die Ungleichung (auch Das große Sieb genannt)

$\sum _{r=1}^R|S({\alpha }_r){|}^2\le (N-1+\frac{1}{\delta })\sum _{M<n\le M+N}|a_n{|}^2.$

Der Faktor $N-1+\frac{1}{\delta }$ kann in dieser Abschätzung nicht verbessert werden. Aufgrund dieser Tatsache gilt die Ungleichung als scharf und sehr mächtig. Das große Sieb hat zahlreiche Anwendungen in der analytischen Zahlentheorie, siehe auch Siebtheorie.

Bohr-Ungleichung

Im Jahr 1914 konnte Harald Bohr zeigen, dass falls die Potenzreihe $f(z)={\sum }_{n=0}^{\mathrm{\infty }}{a}_n{z}^n$ in der Einheitskreisscheibe $𝔼=\{z\in ℂ:|z|<1\}$ konvergiert und die holomorphe Funktion $|f(z)|<1$ in $𝔼$ erfüllt, bereits

$\sum _{n=0}^{\mathrm{\infty }}\frac{|a_n|}{6^n}\le 1$

gilt. Dass sogar ${\sum }_{n=0}^{\mathrm{\infty }}\frac{|a_n|}{3^n}\le 1$ gilt und $r=\frac{1}{3}$ der größtmögliche Bohr-Radius ist, konnte unabhängig von Friedrich Wilhelm Wiener, Marcel Riesz und Issai Schur gezeigt werden.

Dualitätsprinzip

Für Einträge $(c_{n,r})$ einer $N\times R$-Matrix und eine reelle Zahl $D\ge 0$ sind die folgenden Aussagen äquivalent:

• $\sum _{r=1}^R{\left|\sum _{n=1}^N{c}_{n,r}{z}_n\right|}^2\le D\sum _{n=1}^N|z_n{|}^2$, für alle komplexen Zahlen $z_1,\dots ,z_N$,
• ${\left|\sum _{r=1}^R\sum _{n=1}^N{c}_{n,r}{z}_n{w}_r\right|}^2\le D\sum _{n=1}^N|z_n{|}^2\sum _{r=1}^R|w_r{|}^2$, für alle komplexen Zahlen $z_1,\dots ,z_N,w_1,\dots ,w_R$,
• $\sum _{n=1}^N{\left|\sum _{r=1}^R{c}_{n,r}{w}_r\right|}^2\le D\sum _{r=1}^R|w_r{|}^2$, für alle komplexen Zahlen $w_1,\dots ,w_R$.

Dies wird auch als Dualitätsprinzip bezeichnet. Eine Folgerung dessen ist die Existenz einer von den $c_{n,r}$ abhängigen Konstanten $D\ge 0$, sodass für alle $z_1,\dots ,z_N$

$\sum _{r=1}^R{\left|\sum _{n=1}^N{c}_{n,r}{z}_n\right|}^2\le D(\sum _{n=1}^N|z_n{|}^2)\underset{||w||=1}{\sup }\sum _{n=1}^N\left|\sum _{r=1}^R{c}_{n,r}{w}_r\right|,$

wobei $||w||:=\sqrt{\sum _{r=1}^R|w_r{|}^2}$. Dabei steht $\sup$ für das Supremum.

Weitere Ungleichungen

Don Zagier zeigte die Ungleichung

$X^2\sum _{k_1=1}^n\sum _{k_2=1}^n|y_{k_1}-y_{k_2}|+Y^2\sum _{j_1=1}^m\sum _{j_2=1}^m|x_{j_1}-x_{j_2}|\le 2XY\sum _{j=1}^m\sum _{k=1}^n|x_j-y_k|$

mit positiven Zahlen $x_j,y_k$, $X:={\sum }_{j=1}^m{x}_j$ und $Y:={\sum }_{k=1}^n{y}_k$. Verwandt hierzu ist die für reelle Zahlen $x_1\le x_2\le \dots \le x_n$ gültige Ungleichung

${(\sum _{j=1}^n\sum _{k=1}^n|x_j-x_k|)}^2\le \frac{2(n^2-1)}{3}(\sum _{j=1}^n\sum _{k=1}^n(x_j-x_k{)}^2),$

die 2003 auch eine Aufgabe in der Internationalen Mathematik-Olympiade war.

Sind $a_1,\dots ,a_n$ positive Zahlen und $\sigma \in S_n$ eine Permutation, so gilt

$\sum _{j=1}^n{a}_j\le \sum _{j=1}^n\frac{a_j^2}{a_{\sigma (j)}}.$

Zudem gilt die Carleman-Ungleichung

$\sum _{j=1}^n(a_1\cdots a_j{)}^{\frac{1}{j}}\le e\sum _{j=1}^n{a}_j$

mit der Eulerschen Zahl $e$.

Spezielle Reihen

Neben der Konvergenz und dem numerischen Wert einer Reihe ist auch der symbolische Wert einer Reihe von Bedeutung. Beispielsweise lassen sich so mathematische Konstanten darstellen und numerisch berechnen. Für wichtige Reihendarstellungen existieren zudem Tabellierungen in Reihentafeln.

Geometrische Reihe

Konvergenz der geometrischen Reihe für $q=\frac{1}{2}$

Es gilt für alle Werte $q=1$ und $N\in \mathbb{N}$ die Formel

$\sum _{n=0}^N{q}^n=\frac{1-q^{N+1}}{1-q}.$

Daraus ergibt sich für $|q|<1$ die geometrische Reihe

$\sum _{n=0}^{\mathrm{\infty }}{q}^n=\frac{1}{1-q}.$

Eine sehr weitreichende Verallgemeinerung der geometrischen Reihe sind die hypergeometrischen Reihen.

Harmonische Reihe

Die harmonische Reihe

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots$

ist divergent. Dies ist ein Beispiel dafür, dass das Nullfolgenkriterium für Konvergenz nur notwendig, aber nicht hinreichend ist. Die Divergenz ist von „logarithmischer Geschwindigkeit“, dies sieht man zum Beispiel durch

$\sum _{n\le x}\frac{1}{n}\sim \underset{1}{\overset{x}{\int }}\frac{\mathrm{d}t}{t}=\log (x)\stackrel{x\to \mathrm{\infty }}{⟶}\mathrm{\infty }.$

Es wurde jedoch die Frage untersucht, was passiert, wenn man die harmonische Reihe „ausdünnt“, also systematisch Summanden weglässt. Man spricht dann von subharmonischen Reihen. Leonhard Euler zeigte, dass auch, wenn man sich nur auf die Menge der Primzahlen beschränkt, immer noch Divergenz vorliegt. Viggo Brun gelang zu Beginn des 20. Jahrhunderts ein Durchbruch, indem er zeigte, dass bei erneuter Einschränkung auf die Komponenten $p$ und $p+2$ von Primzahlzwillingen $(p,p+2)$, die Reihe konvergent ist:

$\sum _{p,p+2\text{Primzahl}}(\frac{1}{p}+\frac{1}{p+2})=(\frac{1}{3}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{7})+(\frac{1}{11}+\frac{1}{13})+(\frac{1}{17}+\frac{1}{19})+(\frac{1}{29}+\frac{1}{31})+\cdots <\mathrm{\infty }.$

Der Grenzwert dieser Reihe ist auch als Brunsche Konstante bekannt. Die Frage, ob Konvergenz nach Wegstreichen von Zahlen mit bestimmten Ziffern in ihrer Dezimalschreibweise vorliegt, ist Gegenstand der Kempner-Reihen. Es kann damit Konvergenz erreicht werden.

Darstellung mathematischer Konstanten

Kreiszahl

Es wurden neben der Leibniz-Reihe

$\pi =4-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{4(-1{)}^n}{2n+1}$

zahlreiche weitere, teils sehr schnell konvergente, Reihendarstellungen für die Kreiszahl $\pi$ gefunden. Von historischer Bedeutung ist etwa das Basler Problem, das nach dem Grenzwert der Reihe $1+\frac{1}{4}+\frac{1}{9}+\cdots$ aller reziproken Quadratzahlen fragte. Leonhard Euler publizierte 1735 in seiner De Summis Serierum Reciprocarum die Lösung:

$\frac{{\pi }^2}{6}=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}.$

Euler konnte allgemein für $k\in \mathbb{N}$ sogar

$(-1{)}^{k-1}\frac{(2\pi {)}^{2k}}{2(2k)!}{B}_{2k}=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^{2k}}$

mit den Bernoulli-Zahlen $B_k$ zeigen. Der Fall ungerader Exponenten ist deutlich schwieriger, und es existieren hier keine geschlossenen Analoga. Allerdings konnte Matyáš Lerch im Jahr 1900 folgende Reihenidentität aufzeigen:

$\frac{7{\pi }^3}{180}=\sum _{n=1}^{\mathrm{\infty }}(\frac{1}{n^3}+\frac{2}{n^3(e^{2\pi n}-1)}).$

Während all diese Reihen vergleichsweise langsam konvergieren, ist die 1914 von Srinivasa Ramanujan veröffentlichte, auf Untersuchungen von elliptischen Funktionen und Modulfunktionen basierende Gleichung zur Berechnung der Kreiszahl gut geeignet:

$\frac{1}{\pi }=\frac{2\sqrt{2}}{9801}\sum _{n=0}^{\mathrm{\infty }}\frac{(4n)!(1103+26390n)}{(n!{)}^{4}396^{4n}}.$

Die Brüder David und Gregory Chudnovsky berechneten mit ihrer Hilfe 2 Milliarden Nachkommastellen von $\pi$ in den frühen neunziger Jahren. Der davon inspirierte Chudnovsky-Algorithmus basiert auf der folgenden verwandten Reihendarstellung:

$\frac{1}{\pi }=\frac{\sqrt{10005}}{4270934400}\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n(6n)!(545140134n+13591409)}{(3n)!(n!{)}^{3}640320^{3n}}.$

1995 entdeckte Simon Plouffe zusammen mit Peter Borwein und David Harold Bailey die Bailey-Borwein-Plouffe-Formel:

$\pi =\sum _{n=0}^{\mathrm{\infty }}\frac{1}{16^n}(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6}).$

Diese Reihe ermöglicht es, die $n$-te Stelle einer binären, hexadezimalen oder einer zu einer beliebigen anderen Zweierpotenz als Basis gehörenden Darstellung von $\pi$ zu berechnen, ohne dass zuvor die $n-1$ vorherigen Ziffernstellen berechnet werden müssen.

Eulersche Zahl

Die Eulersche Zahl $e=2,718\dots$ ist die Basis des natürlichen Logarithmus. Ihre bekannteste Reihendarstellung ergibt sich aus der Taylor-Entwicklung der natürlichen Exponentialfunktion:

$e=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}=1+1+\frac{1}{2}+\frac{1}{6}+\frac{1}{24}+\frac{1}{120}+\cdots .$

Aufgrund ihrer schnellen Konvergenz ist diese Reihe nicht nur zur Berechnung von Dezimalstellen der Eulerschen Zahl geeignet. Es kann mit ihrer Hilfe auch ein elementarer Beweis erbracht werden, dass $e$ eine irrationale Zahl ist. Allerdings reicht die Konvergenzgeschwindigkeit bei Weitem nicht aus, die Transzendenz von $e$ nachzuweisen (im Gegensatz etwa zur Liouvilleschen Konstanten), und für den Beweis dieser Aussage sind speziellere Techniken vonnöten.

Weitere Konstanten

Für zahlreiche weitere mathematische Konstanten existieren diverse Reihendarstellungen. Zum Beispiel geht die Reihendarstellung

$\sqrt{2}=1+\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n-1}}{2^{2n}(2n-1)}(\genfrac{}{}{0ex}{}{2n}{n})=1+\frac{1}{2}-\frac{1}{2\cdot 4}+\frac{1\cdot 3}{2\cdot 4\cdot 6}-\cdots$

mit den zentralen Binomialkoeffizienten $(\genfrac{}{}{0ex}{}{2n}{n})$ auf Isaac Newton zurück.

Roger Apéry nutzte im Jahr 1979 die Reihe

$\zeta (3)=\frac{5}{2}\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n^3(\genfrac{}{}{0ex}{}{2n}{n})},$

um die Irrationalität von $\zeta (3)$, der Apéry-Konstante, zu zeigen. Es gilt hingegen auch

$\zeta (2)=3\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2(\genfrac{}{}{0ex}{}{2n}{n})},\zeta (4)=\frac{36}{17}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^4(\genfrac{}{}{0ex}{}{2n}{n})}.$

Reihen dieser Art werden auch als Apéry-Reihen bezeichnet. In dem Wunsche, Apérys Beweismethode gegebenenfalls auch auf andere Zeta-Werte anwenden zu können, sind diese bis heute Gegenstand intensiver Forschung. Beiträge lieferten unter anderem Ablinger, Bailey, Borwein, Sun und Zucker. Beim Versuch einer Verallgemeinerung stößt man natürlicherweise auf Verbindungen zu allgemeinen harmonischen Summen und multiplen Polylogarithmen. Doch trotz Formeln wie zum Beispiel

$\zeta (7)=\frac{5}{2}\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n^7(\genfrac{}{}{0ex}{}{2n}{n})}+\frac{25}{2}\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n^3(\genfrac{}{}{0ex}{}{2n}{n})}\sum _{k=1}^{n-1}\frac{1}{k^4}$

steht der Durchbruch bis heute aus. In diesem Kontext ist auch die Reihe

$\log (\mathrm{\Phi }{)}^2=\frac{1}{2}\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n^2(\genfrac{}{}{0ex}{}{2n}{n})}$

mit dem natürlichen Logarithmus des Goldenen Schnittes $\mathrm{\Phi }$ bemerkenswert.

Reihen mit rationalen Gliedern sind für die Euler-Mascheroni-Konstante $\gamma$ vergleichsweise schwer zu finden. Ein berühmtes Beispiel ist eine von Giovanni Enrico Eugenio Vacca gegebene Reihe

$\gamma =\sum _{n=2}^{\mathrm{\infty }}(-1{)}^n\frac{\lfloor {\log }_2(n)\rfloor }{n}=\frac{1}{2}-\frac{1}{3}+2(\frac{1}{4}-\frac{1}{5}+\frac{1}{6}-\frac{1}{7})+3(\frac{1}{8}-\dots -\frac{1}{15})+\dots$

aus dem Jahr 1910. Es bedeutet $\lfloor \rfloor$ die Gaußklammer.

Summenformeln und Transformationen

Partielle Summation

Sind die Glieder von Reihen, bzw. ihrer Partialsummen, von der Gestalt $a_n{b}_n$, so kann durch Umordnung „partiell summiert“ werden. Etwa gilt für $N\in \mathbb{Z}$ und $M\in \mathbb{N}$

$\sum _{n=N+1}^{N+M}{a}_n{b}_n=A_{N+M}{b}_{N+M+1}+\sum _{n=N+1}^{N+M}{A}_n(b_n-b_{n+1}),$ wobei $A_n:=\sum _{m=N+1}^n{a}_m$.

Dies bezeichnet man auch als Abelsche partielle Summation. Bestätigen lässt sich dies durch sukzessives Ausmultiplizieren und Verrechnen der Terme. Trotz ihrer Einfachheit erweist sich die partielle Summation als sehr hilfreich in vielen Situationen. Sie kommt vor allem dann zum Einsatz, wenn die Zahlen $a_n$ „schwanken“ (etwa ständige Vorzeichenwechsel), womit deren Summen $A_n$ verhältnismäßig klein sind, während die Zahlen $b_n$ sukzessive kleiner werden, da dann die Differenzen $b_n-b_{n+1}$ eventuell viel schneller gegen Null streben als die $b_n$ selbst. Zum Beispiel ist sie dazu geeignet, die Existenz einer Abszisse bedingter Konvergenz für Dirichletreihen zu zeigen.

Eine Variante der partiellen Summation ist die Identität

$\sum _{k=0}^n{a}_k(b_{k+1}-b_k)+\sum _{k=1}^n{b}_k(a_k-a_{k-1})=a_n{b}_{n+1}-a_0{b}_0.$

Eine weitere Variante betrifft den Fall, dass $b_n=f(n)$ mit einem auf dem Intervall $[1,x]$ stetig differenzierbaren $f$. Dann gilt mit $A(t):=\sum _{1\le n\le t}{a}_n$

$\sum _{1\le n\le x}{a}_{n}f(n)=A(x)f(x)-\underset{1}{\overset{x}{\int }}A(t)f^{\prime }(t)\mathrm{d}t.$

Diese Transformation ist dann hilfreich, wenn $A(x)$ durch „Schwankungen“ der Summanden verhältnismäßig klein ist, während $f^{\prime }$ „schnell“ gegen Null geht. Ein Beispiel ist $f(x)=\frac{1}{x}$, dessen Ableitung für $x\to \mathrm{\infty }$ sogar quadratisch gegen Null strebt. Dies führt zum Spezialfall

$\sum _{1\le n\le x}\frac{a_n}{n}=\frac{A(x)}{x}+\underset{1}{\overset{x}{\int }}\frac{A(t)}{t^2}\mathrm{d}t.$

Integralvergleich

Ist $f$ eine reellwertige, monotone Funktion auf dem Intervall $[M,N]$ mit ganzen $M<N$, so existiert eine Konstante $\vartheta =\vartheta (M,N)\in [0,1]$, sodass

$\sum _{n=M+1}^{N}f(n)=\underset{M}{\overset{N}{\int }}f(x)\mathrm{d}x+\vartheta \cdot (f(N)-f(M)).$

Euler-Maclaurin-Formel

Eine Möglichkeit, eine Reihe auszuwerten oder anzunähern, bietet die Euler-Maclaurin-Summenformel. Diese drückt Summen explizit in der Sprache der Integralrechnung aus und ist allgemein gegeben durch:

$\begin{array}{cc}\sum _{n=N}^{M}f(n)=& \underset{N}{\overset{M}{\int }}f(x)\mathrm{d}x+\frac{f(M)+f(N)}{2}+\sum _{k=1}^{\lfloor p/2\rfloor }\frac{B_{2k}}{(2k)!}(f^{(2k-1)}(M)-f^{(2k-1)}(N))+(-1{)}^{p+1}\underset{N}{\overset{M}{\int }}{f}^{(p)}(x)\frac{B_p(x-\lfloor x\rfloor )}{p!}\mathrm{d}x.\end{array}$

Hierbei ist $f$ eine auf dem Intervall $(N,M)$ mindestens $p$-mal differenzierbare Funktion und $p\ge 1$ eine natürliche Zahl. Es bezeichnen zudem $B_k$ die Bernoulli-Zahlen, $B_{\nu }(x)$ die Bernoulli-Polynome und $\lfloor x\rfloor$ den ganzzahligen Anteil von $x$. Die ersten Formen haben die Gestalt: $$\begin{array}{cc}\sum _{n=N}^{M}f(n)-\underset{N}{\overset{M}{\int }}f(x)\mathrm{d}x& =\frac{f(M)+f(N)}{2}+\underset{N}{\overset{M}{\int }}{f}^{\prime }(x)(x-\lfloor x\rfloor -\frac{1}{2})\mathrm{d}x\\ & =\frac{f(M)+f(N)}{2}+\frac{1}{6}\frac{f^{\prime }(M)-f^{\prime }(N)}{2!}-\underset{N}{\overset{M}{\int }}{f}^{″}(x)\frac{P_2(x)}{2!}\mathrm{d}x\\ & =\frac{f(M)+f(N)}{2}+\frac{1}{6}\frac{f^{\prime }(M)-f^{\prime }(N)}{2!}+\underset{N}{\overset{M}{\int }}{f}^{‴}(x)\frac{P_3(x)}{3!}\mathrm{d}x\\ & =\frac{f(M)+f(N)}{2}+\frac{1}{6}\frac{f^{\prime }(M)-f^{\prime }(N)}{2!}-\frac{1}{30}\frac{f^{‴}(M)-f^{‴}(N)}{4!}-\underset{N}{\overset{M}{\int }}{f}^{(4)}(x)\frac{P_4(x)}{4!}\mathrm{d}x\\ & =\frac{f(M)+f(N)}{2}+\frac{1}{6}\frac{f^{\prime }(M)-f^{\prime }(N)}{2!}-\frac{1}{30}\frac{f^{‴}(M)-f^{‴}(N)}{4!}+\underset{N}{\overset{M}{\int }}{f}^{(5)}(x)\frac{P_5(x)}{5!}\mathrm{d}x\\ & =\frac{f(M)+f(N)}{2}+\frac{1}{6}\frac{f^{\prime }(M)-f^{\prime }(N)}{2!}-\frac{1}{30}\frac{f^{‴}(M)-f^{‴}(N)}{4!}+\frac{1}{42}\frac{f^{(5)}(M)-f^{(5)}(N)}{6!}-\underset{N}{\overset{M}{\int }}{f}^{(6)}(x)\frac{P_6(x)}{6!}\mathrm{d}x\\ & =\frac{f(M)+f(N)}{2}+\frac{1}{6}\frac{f^{\prime }(M)-f^{\prime }(N)}{2!}-\frac{1}{30}\frac{f^{‴}(M)-f^{‴}(N)}{4!}+\frac{1}{42}\frac{f^{(5)}(M)-f^{(5)}(N)}{6!}+\underset{N}{\overset{M}{\int }}{f}^{(7)}(x)\frac{P_7(x)}{7!}\mathrm{d}x,\end{array}$$ wobei abkürzend $P_{\nu }(x):=B_{\nu }(x-\lfloor x\rfloor )$.

Eine Anwendung dieser Summenformel ist die effiziente Berechnung der Partialsummen konvergenter oder auch divergenter Reihen. Ein Beispiel ist die harmonische Reihe:

$\sum _{m=1}^n\frac{1}{m}=\log (n)+\gamma +\frac{1}{2n}-\frac{1}{12n^2}+\frac{{\vartheta }_n}{60n^4}$

mit der Euler-Mascheroni-Konstanten $\gamma$ und einer beschränkten Folge ${\vartheta }_n\in [0,1]$. Zum Beispiel ist

$H_{1000}=1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{1000}=7,4854708605503449126\dots ,$ und $\log (1000)+\gamma +\frac{1}{2000}-\frac{1}{12000000}=7,4854708605503365793\dots .$

Abel-Plana-Summenformel

Ähnlichkeit zur Euler-Maclaurin-Summenformel hat die Abel-Plana-Summenformel. Sei $f(z)$ holomorph für $m\le \mathrm{R}\mathrm{e}(z)\le n$ mit $m,n\in {\mathbb{N}}_0$ und $m\le n$. Man nehme an, dass

$\underset{y\to \mathrm{\infty }}{\lim }|f(x\pm iy)|e^{-2\pi y}=0,$

gleichmäßig für $m\le x\le n$. Dann gilt

$\sum _{k=m}^{n}f(k)=\underset{m}{\overset{n}{\int }}f(x)\mathrm{d}x+\frac{f(m)+f(n)}{2}-i\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{f(n+iu)-f(n-iu)-f(m+iu)+f(m-iu)}{e^{2\pi u}-1}\mathrm{d}u.$

Die Poissonsche Summationsformel

Klassisch

Gelten für $f:ℝ\to ℂ$ geeignete Wachstumsbedingungen, ist es zum Beispiel eine Schwartz-Funktion, so gilt ferner die Poissonsche Summenformel:

$\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}f(n)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\hat{f}(n).$

Diese ermöglicht es, eine Reihe über Funktionswerte an ganzen Stellen in jene bezüglich der Fourier-Transformierten

$\hat{f}(x):=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(y)e^{-2\pi ixy}\mathrm{d}y$

umzuwandeln, und umgekehrt. Benutzt wird diese Summenformel unter anderem beim Nachweis der Transformationsformel für die Jacobische Theta-Reihe.

Verwandt dazu ist der folgende Satz. Ist $\alpha ,\beta >0$ mit $\alpha \beta =\pi$, und $\phi :[0,\mathrm{\infty })\to ℂ$ eine stetige Funktion mit endlicher Variation auf $(0,\mathrm{\infty })$, die über $(0,\mathrm{\infty })$ integrierbar ist, so gilt für

$\psi (r):=\underset{0}{\overset{\mathrm{\infty }}{\int }}\phi (x)\cos (rx)\mathrm{d}x$

bereits

$\alpha (\frac{\phi (0)}{2}+\sum _{k=1}^{\mathrm{\infty }}\phi (\alpha k))=\psi (0)+2\sum _{k=1}^{\mathrm{\infty }}\psi (\beta k).$

Verallgemeinerungen

Die Poisson’sche Summationsformel kann sehr weitreichend verallgemeinert werden. Zu Grunde liegen Folgen $a_n$, die besondere Eigenschaften mitbringen müssen:

1. Die zugehörige Dirichlet-Reihe $L(a;s):=\sum _{n=1}^{\mathrm{\infty }}{a}_n{n}^{-s}$ konvergiert für alle $s$ mit $\mathrm{R}\mathrm{e}(s)>1$, besitzt eine holomorphe Fortsetzung nach $ℂ\setminus \{1\}$ und hat einen Pol der Ordnung $r\ge 0$ in $s=1$.
2. Die Komplettierung $\mathrm{\Lambda }(a;s):=\gamma (s)L(a;s)$ erfüllt eine Funktionalgleichung $\mathrm{\Lambda }(a;s)=w\mathrm{\Lambda }(a^{*};1-s)$, wobei $a_n^{*}$ eine andere – zu $a_n$ „duale“ – Folge ist und $w$ eine komplexe Zahl mit $|w|=1$. Es ist zudem $\gamma (s):=A^s\prod _{j=1}^g\mathrm{\Gamma }(b_{j}s+c_j)$ für positive $A,b_j$ (mit der Gammafunktion $\mathrm{\Gamma }(s)$) ein sog. „Gammafaktor“, und für $a_n^{*}$ wird all dies analog definiert (mit Gammafaktor ${\gamma }^{*}(s)$ etc.).

Gelten dann alle Notationen wie oben, und setzt man für $0<c<1$

$K(x):=\frac{1}{2\pi i}\underset{c-i\mathrm{\infty }}{\overset{c+i\mathrm{\infty }}{\int }}\frac{\gamma (s)}{\gamma (1-s)}{x}^{-s}\mathrm{d}x$ und $g(x):=\underset{0}{\overset{\mathrm{\infty }}{\int }}f(t)K(xt)\mathrm{d}t,$

so gilt

$\sum _{n=0}^{\mathrm{\infty }}{a}_{n}f(n)={\mathrm{r}\mathrm{e}\mathrm{s}}_{s=1}(L(a;s)\underset{0}{\overset{\mathrm{\infty }}{\int }}f(t)t^{s-1}\mathrm{d}t)+w\sum _{n=1}^{\mathrm{\infty }}{a}_n^{*}g(n),$

vorausgesetzt, alle Ausdrücke konvergieren. Es bezeichnet ${\mathrm{r}\mathrm{e}\mathrm{s}}_{s=1}$ dabei das Residuum an der Stelle $s=1$.

Beispiele für diesen Formalismus sind:

Ist $a_n=1$, so gilt $L(a;s)=\zeta (s)$ mit der Riemannschen Zeta-Funktion. Setzt man $\gamma (s):={\pi }^{-\frac{s}{2}}\mathrm{\Gamma }(s)$, ist diese wegen ihrer Funktionalgleichung selbst-dual. Es gilt ferner

$\underset{0}{\overset{\mathrm{\infty }}{\int }}\cos (2\pi x)x^{s-1}\mathrm{d}x=(2\pi {)}^{-s}\cos \left(\frac{\pi s}{2}\right)\mathrm{\Gamma }(s),$

aber gleichzeitig auch

$\frac{\gamma (s)}{\gamma (1-s)}=2(2\pi {)}^{-s}\cos \left(\frac{\pi s}{2}\right)\mathrm{\Gamma }(s)$

mit dem Eulerschen Ergänzungssatz sowie der Duplikationsformel für die Gammafunktion. Damit ergibt sich $K(x)=2\cos (2\pi x)$ und für gerade Funktionen $f$

$\sum _{n=1}^{\mathrm{\infty }}f(n)+\frac{f(0)}{2}=\underset{0}{\overset{\mathrm{\infty }}{\int }}f(x)\mathrm{d}x+2\sum _{n=1}^{\mathrm{\infty }}\underset{0}{\overset{\mathrm{\infty }}{\int }}f(t)\cos (2\pi nt)\mathrm{d}t,$

was eine Variante der Poisson’schen Summationsformel ist.

Van der Corputsche Summenformel

Sei $\eta >0$ vorgegeben. Dann gibt es eine Konstante $C(\eta )>0$ mit folgender Eigenschaft: Für $b>a$ seien $f:[a,b]\to ℝ$ und $g:[a,b]\to [0,\mathrm{\infty })$ stetig differenzierbare Funktionen. Es seien $f^{\prime }$, $g$ und $|g^{\prime }|$ monoton fallend. Dann gilt

$\sum _{a<n\le b}g(n)e^{2\pi if(n)}=\sum _{f^{\prime }(b)-\eta <h<f^{\prime }(a)+\eta }\underset{a}{\overset{b}{\int }}g(\xi )e^{2\pi i(f(\xi )-h\xi )}\mathrm{d}\xi +R,$

mit der Restgliedabschätzung

$|R|\le C(\eta )(|g^{\prime }(a)|+g(a)\log (|f^{\prime }(a)|+|f^{\prime }(b)|+2)).$

Perronsche Formel

Die Perronsche Formel behandelt Folgen $a_n$, die höchstens polynomiell anwachsen. Sie stellt eine Verbindung der Partialsummen $\sum _{n\le x}{a}_n$ zu der Dirichlet-erzeugenden Funktion ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n{n}^{-s}$ über Kurvenintegrale her.

Es sei $F(s):={\sum }_{n=1}^{\mathrm{\infty }}{a}_n{n}^{-s}$ eine Dirichlet-Reihe, die irgendwo konvergiert, ${\sigma }_c$ ihre Konvergenzabszisse. Für jedes $x\in ℝ\setminus \mathbb{N}$ definiert man die summatorische Funktion

$A^{*}(x)=\sum _{n<x}{a}_n+\frac{1}{2}{a}_x$

wobei $a_x$ für alle nicht-natürlichen $x$ einfach 0 ist. Dann gilt für $\kappa >\max (0,{\sigma }_c)$ die Formel

$A^{*}(x)=\frac{1}{2\pi i}\underset{\kappa -i\mathrm{\infty }}{\overset{\kappa +i\mathrm{\infty }}{\int }}F(s)x^s\frac{\mathrm{d}s}{s},$

wobei das Integral im Falle von $x\in {ℝ}_{>0}\setminus \mathbb{N}$ bedingt konvergiert und für $x\in \mathbb{N}$ im Sinne des Cauchyschen Hauptwertes existiert.

Mellintransformation

Srinivasa Ramanujan, der für seine starke analytische Intuition bekannt ist, machte laut Godfrey Harold Hardy „intensiven Gebrauch“ von der Formel

$\underset{0}{\overset{\mathrm{\infty }}{\int }}{x}^{s-1}[\varphi (0)-\varphi (1)x+\varphi (2)x^2-\cdots ]\mathrm{d}x=\frac{\pi }{\sin (\pi s)}\varphi (-s).$

Eine äquivalente Form ist

$\underset{0}{\overset{\mathrm{\infty }}{\int }}{x}^{-s}[\varphi (1)-\varphi (2)x+\varphi (3)\frac{x^2}{2!}-\varphi (4)\frac{x^3}{3!}+\cdots ]\mathrm{d}x=\mathrm{\Gamma }(1-s)\varphi (s).$

Dabei bezeichnet $\mathrm{\Gamma }(s)$ die Gammafunktion. Diese Identitäten sind jedoch nur formal zu verstehen, und Konvergenz liegt nur unter bestimmten Voraussetzungen vor. Hardy gab schließlich strenge Kriterien: Es sei $s=\sigma +it$ und $H_{\delta }:=\{s\in ℂ:\mathrm{R}\mathrm{e}(s)\ge -\sigma \}$, wobei $0<\delta <1$ fest gewählt ist. Man nehme an, dass $\varphi (s)$ holomorph im Bereich $H_{\delta }$ ist, und es Konstanten $C,P$ und $A<\pi$ gibt mit

$|\varphi (s)|\le C{e}^{P\sigma +A|t|}$

für alle $s\in H_{\delta }$. Für $x>0$ und $0<c<\delta$ definiere man

$\mathrm{\Phi }(x):=\frac{1}{2\pi i}\underset{c-i\mathrm{\infty }}{\overset{c+i\mathrm{\infty }}{\int }}\frac{\pi }{\sin (\pi s)}\varphi (-s)x^{-s}\mathrm{d}s.$

Im Fall $0<x<e^{-P}$ gilt die Reihendarstellung

$\mathrm{\Phi }(x)=\sum _{k=0}^{\mathrm{\infty }}\varphi (k)(-x{)}^k.$

Dann gilt für $0<\sigma <\delta$

$\underset{0}{\overset{\mathrm{\infty }}{\int }}\mathrm{\Phi }(x)x^{s-1}\mathrm{d}x=\frac{\pi }{\sin (\pi s)}\varphi (-s).$

Allgemeiner ist die Mellintransformation in der Lage, Potenzreihen in Dirichletreihen überzuführen.

Möbiussche Umkehrformel

Sind $F$ und $G$ reell- oder komplexwertige Funktionen auf $[1,\mathrm{\infty })$, und ist

$G(x)=\sum _{1\le n\le x}F\left(\frac{x}{n}\right)$ (für alle $x\ge 1$),

so lässt sich $F$ aus $G$ „rekonstruieren“ durch

$F(x)=\sum _{1\le n\le x}\mu (n)G\left(\frac{x}{n}\right)$ (für alle $x\ge 1$).

Dabei bezeichnet $\mu$ die Möbiusfunktion aus der Zahlentheorie. Die Summationsschranken können unter der Fortsetzung von $F$ und $G$ auf $[0,\mathrm{\infty })$ via $F(x)=G(x)=0$ für alle $0\le x<1$ weggelassen werden. In diesem Fall folgt aus $G(x)={\sum }_{n=1}^{\mathrm{\infty }}F(\frac{x}{n})$ stets $F(x)={\sum }_{n=1}^{\mathrm{\infty }}\mu (n)G(\frac{x}{n})$.

Eine Variante dieser Umkehrformel betrifft Dirichletreihen. Es gilt

$g(x)=\sum _{m=1}^{\mathrm{\infty }}\frac{f(mx)}{m^s}$ (für alle $x\ge 1$) $⟺f(x)=\sum _{m=1}^{\mathrm{\infty }}\mu (m)\frac{g(mx)}{m^s}$ (für alle $x\ge 1$)

für alle $s\in ℂ$, sodass beide Reihen für alle $x\in [1,\mathrm{\infty })$ absolut konvergieren.

Reihentransformationen

Es zeigte Sarvadaman Chowla eine Identität zwischen Reihen periodischer Funktionen. Ist $c_n=O(n^{\varphi })$ eine Folge mit $\varphi <\frac{1}{3}$, so gilt für fast alle reellen $\theta$ (also alle bis auf Nullmenge)

$\sum _{n=1}^{\mathrm{\infty }}\frac{c_n}{n}\{n\theta \}=-\frac{1}{\pi }\sum _{n=1}^{\mathrm{\infty }}\frac{G_n}{n}\sin (2\pi n\theta ),$

wobei $G_n=\sum _{d|n}{c}_d$ mit $\{\theta \}=\theta -\lfloor \theta \rfloor -\frac{1}{2}$. Es bedeutet $\lfloor \rfloor$ die Gaußklammer. Ein Spezialfall dieser Identität ist, mit $c_1=1$ und $c_n=0$ für alle $n>1$,

$\{\theta \}=-\frac{1}{\pi }\sum _{n=1}^{\mathrm{\infty }}\frac{\sin (2\pi in\theta )}{n},(\theta \notin \mathbb{Z}).$

In manchen Fällen kann Konvergenz beschleunigt werden. Dazu kann die Reihe in eine andere transformiert werden. Ein Beispiel ist die Eulersche Reihentransformation. Ist

$\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k{a}_k$

eine beliebige konvergente Reihe, so ist stets

$\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k{a}_k=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{2^{n+1}}\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})a_k.$

Eine Anwendung ist

$\frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots =\frac{1}{2}(1+\frac{1}{3}+\frac{1\cdot 2}{3\cdot 5}+\frac{1\cdot 2\cdot 3}{3\cdot 5\cdot 7}+\cdots ).$

Asymptotische Analysis und Taubersätze

Asymptotik von Reihen mit holomorphen Gliedern

In manchen Anwendungen ist es vonnöten, Reihen der Gestalt $g(z)={\sum }_{n=1}^{\mathrm{\infty }}f(nz)$ für $z\to 0^{+}$ (in einem Winkelbereich) zu verstehen. Erfüllt $f$ gewisse Eigenschaften, darunter Holomorphie, kann dies bewerkstelligt werden. Im Folgenden sei stets $D_{\theta }:=\{r{e}^{i\alpha }:r\ge 0,|\alpha |\le \theta \}$ mit einem $0\le \theta <\frac{\pi }{2}$.

Es sei nun $f:ℂ\to ℂ$ eine Funktion, die in einer Umgebung von $D_{\theta }$ holomorph ist, insbesondere im Ursprung. Ferner gebe es für jedes $k\in {\mathbb{N}}_0$ ein $\epsilon >0$, sodass $f(w)=O(w^{-1-\epsilon }),$ wenn $|w|\to \mathrm{\infty }$ in $D_{\theta }$. Dann gilt für alle $a\in ℝ$ und $N\in {\mathbb{N}}_0$:

$\sum _{m=0}^{\mathrm{\infty }}f(w(m+a))=\frac{1}{w}\underset{0}{\overset{\mathrm{\infty }}{\int }}f(x)\mathrm{d}x-\sum _{n=0}^{N-1}\frac{B_{n+1}(a)f^{(n)}(0)}{(n+1)!}{w}^n+O_N(w^N)$

gleichmäßig, sofern $w\to 0$ in $D_{\theta }$. Dabei bezeichnen $B_n(x)$ die Bernoulli-Polynome und $O_N$ das Landau-Symbol (die Konstante hängt nur von der Wahl von $N$ ab). Die Aussage lässt sich sogar auf den Fall verallgemeinern, dass $f$ einen einfachen Pol im Ursprung mit Residuum $b_{-1}$ hat. Gelten sonst alle Voraussetzungen wie oben, so gilt in dieser Situation für $a\in ℝ\setminus (-{\mathbb{N}}_0)$

$\sum _{m=0}^{\mathrm{\infty }}f(w(m+a))=\frac{b_{-1}\mathrm{Log}(\frac{1}{w})}{w}+\frac{b_{-1}(1-a)}{w}\sum _{m=0}^{\mathrm{\infty }}\frac{1}{(m+a)(m+1)}+\frac{1}{w}\underset{0}{\overset{\mathrm{\infty }}{\int }}(f(x)-\frac{b_{-1}{e}^{-x}}{x})\mathrm{d}x-\sum _{n=0}^{N-1}\frac{B_{n+1}(a)f^{(n)}(0)}{(n+1)!}{w}^n+O_N(w^N)$

gleichmäßig, sofern $w\to 0$ in $D_{\theta }$.

Taubersatz von Wiener-Ikahara

Der Satz von Wiener-Ikahara trifft manchmal Aussagen über Summen $\sum _{n\le x}{a}_n$, wenn die Reihe ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n{n}^{-s}$ gewisse Eigenschaften hat. Im Jahre 1954 konnte Delange den Satz von Wiener-Ikehara deutlich verallgemeinern, nämlich auf Singularitäten gemischten Typs. Es sei $F(s)={\sum }_{n=1}^{\mathrm{\infty }}{a}_n{n}^{-s}$ eine Dirichlet-Reihe mit nicht-negativen Koeffizienten, die auf einer Halbebene $\mathrm{R}\mathrm{e}(s)>\sigma >0$ konvergiert. Man nehme an, $F$ lasse sich mit Ausnahme des Punktes $s=\sigma$ holomorph auf die gesamte Gerade $\mathrm{R}\mathrm{e}(s)=\sigma$ fortsetzen und dass es sich in einer kleinen Umgebung um $s=\sigma$ in der Form

$F(s)=\frac{1}{(s-\sigma {)}^{w+1}}\sum _{j=0}^q{g}_j(s){\{\log \left(\frac{1}{s-\sigma }\right)\}}^j+g(s)$

schreiben lässt, wobei $w$ eine reelle Zahl und die Funktionen $g_j$ und $g$ holomorph sind mit $g_q(\sigma )=0$. Dann gilt: Ist $w$ keine negative ganze Zahl, so folgt

$\sum _{n\le x}{a}_n\sim \frac{g_q(\sigma )}{\sigma \mathrm{\Gamma }(w+1)}{x}^{\sigma }(\log (x){)}^w(\log (\log (x)){)}^q,$

und ist es eine negative ganze Zahl $w=-m-1$ und $q\ge 1$:

$\sum _{n\le x}{a}_n\sim (-1{)}^{m}m!\frac{q{g}_q(\sigma )}{\sigma }\frac{x^{\sigma }(\log (\log (x)){)}^{q-1}}{(\log (x){)}^{m+1}}.$

Dabei bedeutet das Symbol $\sim$, dass beide Seiten für wachsende Werte $x$ asymptotisch gleich schnell anwachsen, ihr Quotient also für $x\to \mathrm{\infty }$ gegen 1 strebt.

Weitere Anwendungen

Unendliche Produkte

Ein unendliches Produkt ${\prod }_{n=1}^{\mathrm{\infty }}{a}_n$ wird, analog zur unendlichen Reihe, als Folge der Partialprodukte

$p_N:=\prod _{n=1}^N{a}_n$

definiert. Allerdings ist der Konvergenzbegriff für unendliche Produkte subtiler; es ist $0$ als Grenzwert nur zugelassen, falls ab einem gewissen $M$ die Partialprodukte ${\prod }_{n=M}^N{a}_n$ für $N\to \mathrm{\infty }$ gegen einen Grenzwert $=0$ konvergieren. Durch Logarithmusbildung bzw. Exponenzierung besteht ein Zusammenhang zwischen unendlichen Produkten und Reihen. So ist ein unendliches Produkt

$\prod _{n=1}^{\mathrm{\infty }}(1+a_n)$

genau dann absolut konvergent (bzw. unbedingt konvergent, der Grenzwert hängt also nicht von der Reihenfolge der Faktoren ab), falls die Reihe ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ absolut konvergiert. ${\prod }_{n=1}^{\mathrm{\infty }}(1+a_n)$ konvergiert, falls ${\sum }_{n=1}^{\mathrm{\infty }}(a_n-\frac{1}{2}{a}_n^2)$ und ${\sum }_{n=1}^{\mathrm{\infty }}|a_n{|}^3$ konvergieren. Andererseits kann besagtes Produkt unter Umständen bedingt konvergieren, selbst wenn ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n$ und ${\sum }_{n=1}^{\mathrm{\infty }}{a}_n^2$ beide divergieren.

Wahrscheinlichkeitstheorie

In der Wahrscheinlichkeitstheorie sind unendliche Reihen unter anderem im Kontext mit stochastischen Prozessen von Bedeutung. Ein Resultat in dieser Richtung ist etwa der kolmogoroffsche Dreireihensatz. Das asymptotische Verhalten der Partialsummen der unendlichen Reihe ${\sum }_{n=1}^{\mathrm{\infty }}{X}_n$ mit gewissen identisch verteilten Zufallsvariablen $X_n$ ist Gegenstand des Gesetzes der großen Zahlen und des zentralen Grenzwertsatzes. Allerdings tauchen sie bereits bei der Axiomatisierung der Wahrscheinlichkeitstheorie durch Kolmogoroff auf: Darin wird verlangt, dass ein Wahrscheinlichkeitsmaß $P$ für eine abzählbare Folge von disjunkten Ereignissen $(A_n{)}_{n\in \mathbb{N}}\subseteq \mathrm{\Omega }$ eines Wahrscheinlichkeitsraums $\mathrm{\Omega }$ stets

$P\left(\bigcup _{n=1}^{\mathrm{\infty }}{A}_n\right)=\sum _{n=1}^{\mathrm{\infty }}P(A_n)$

erfüllen muss. Die Reihe zur Rechten ist dabei stets absolut konvergent mit einem Grenzwert in $[0,1]$, da das Maß nicht-negativ und monoton ist und zudem $P(\mathrm{\Omega })=1$ verlangt wird. Eine Verallgemeinerung auf Ebene endlicher Vereinigungen ist die Inklusions-/Exklusionsformel, die für beliebige Ereignisse $A_1,\dots ,A_n$ gilt:

$P(A_1\cup A_2\cup \dots \cup A_n)=\sum _{k=1}^n(-1{)}^{k-1}\sum _{1\le j_1<\dots <j_k\le n}P(A_{j_1}\cap \dots \cap A_{j_k}).$

In Kontexten der probabilistischen Zahlentheorie untersuchte unter anderem Emmanuel Kowalski Zufallsreihen.

Finanzmathematik

Annuitätendarlehen sind das gängigste Modell zur Finanzierung privater Immobilien. Zwischen Kreditgeber und -nehmer werden ein Zinssatz, eine monatlich zu zahlende Rate und eine Laufzeit vereinbart. Am Ende der Laufzeit bleibt eine Restschuld, für die dann ein neuer Kreditvertrag abgeschlossen wird, wobei die Zinsrate an die aktuelle Geldmarktsituation angepasst wird. Um das Risiko zu kennen, ist es ergo für jeden Hausbauer wichtig, die Restschuld zu bestimmen.

Es bezeichnen $K$ die Kreditsumme, $R$ die monatliche Rate und $p$ die jährliche Zinsrate. Die nach $n$ Monaten noch verbleibende Restschuld sei $a_n$. Die im $n$-ten Monat zu entrichtenden Zinsen werden im Bankwesen zu $\left(\frac{p}{12}\right)a_{n-1}$ bestimmt. Die $a_n$ folgen mit $a_0:=K$ der Rekursion

$a_n=a_{n-1}\underset{:=c}{\underbrace{(1+\frac{p}{12})}}-R.$

Unter Betrachtung der erzeugenden Funktion der $a_n$ kann unter Ausnutzung dieser Rekursion

$f(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n=K+\sum _{n=1}^{\mathrm{\infty }}(c{a}_{n-1}-R)x^n$

gezeigt werden, und durch einige Umformungen erhält man

$f(x)=\sum _{n=0}^{\mathrm{\infty }}(K{c}^n-R\frac{1-c^n}{1-c})x^n.$

Durch Koeffizientenvergleich erhält man damit die geschlossene Formel

$a_n=K{c}^n-R\frac{1-c^n}{1-c}.$

Zahlentheorie

Reihen haben auch bedeutende Anwendung in der analytischen Zahlentheorie. So kann es in vielen Fällen helfen, einer zu untersuchenden zahlentheoretischen Funktion $a_n$ die erzeugenden Funktionen

$F(z):=\sum _{n=0}^{\mathrm{\infty }}{a}_n{z}^n$ oder $f(s):=\sum _{n=1}^{\mathrm{\infty }}\frac{a_n}{n^s}$

zuzuordnen. Mit Hilfe von Tauber-Sätzen, Integraltransformationen (wie der Perronschen Formel) oder der Kreismethode können dann gegebenenfalls detaillierte Aussagen über das langfristige Verhalten der $a_n$ getroffen werden. Handelt es sich bei $F(z)$ sogar (im Wesentlichen) um eine Modulform, kann in bestimmten Fällen eine exakte Formel in Form einer unendlichen Reihe für die $a_n$ hergeleitet werden. Dies ist etwa bei der Partitionsfunktion der Fall:

$p(n)=\frac{2\pi }{(24n-1{)}^{\frac{3}{4}}}\sum _{k=1}^{\mathrm{\infty }}\frac{A_k(n)}{k}{I}_{\frac{3}{2}}\left(\frac{\pi \sqrt{24n-1}}{6k}\right),$

wobei $I_{\frac{3}{2}}$ die Bessel-Funktion und $A_k$ eine sog. Kloosterman-Summe bezeichnet.

Auch bei Dichteresultaten, etwa im Umfeld der Duffin-Schaeffer-Vermutung oder des Satzes von Green-Tao, spielen unendliche Reihen eine zentrale Rolle. Die Duffin-Schaeffer-Vermutung besagt, dass für jede Funktion $f:\mathbb{N}\to (0,\mathrm{\infty })$ die Ungleichung

$|\alpha -\frac{p}{q}|<\frac{f(q)}{q}$

für fast alle $\alpha \in [0,1]$ (im Sinne des Lebesgue-Maßes) für unendlich viele teilerfremde $q>p>0$ lösbar ist, genau dann, wenn

$\sum _{q=1}^{\mathrm{\infty }}\frac{\phi (q)f(q)}{q}=\mathrm{\infty }.$

Dabei ist $\phi (q)$ die Eulersche Phi-Funktion. Gilt hingegen ${\sum }_{q=1}^{\mathrm{\infty }}\frac{\phi (q)f(q)}{q}<\mathrm{\infty }$, so ist die entsprechende Ungleichung fast sicher nicht unendlich oft erfüllt. Aus probabilistischer Sicht handelt es sich um ein Null-Eins-Gesetz. Während diese letzte Richtung über Argumente des Borel-Cantelli-Lemmas recht schnell ersichtlich ist, galt die andere Richtung, also aus der Reihendivergenz die fast sichere unendlich frequentierte Lösbarkeit zu folgern, lange als extrem schwieriges zahlentheoretisches Problem. Ein vollständiger Beweis der Vermutung konnte erst 2019 durch Dimitris Koukoulopoulos und James Maynard erbracht werden. Eine Abschwächung der Vermutung war bereits als Satz von Chintschin bekannt, wobei die Beweise hier vergleichsweise elementar sind. Darüber hinaus „messen“ Reihen in gewisser Weise „ab“, wie dicht gewisse arithmetische Objekte, etwa Primzahlen, in anderen Objekten verteilt sind. Verwandt zum Satz von Green-Tao, der besagt, dass die Folge der Primzahlen beliebig lange arithmetische Progressionen enthält, ist eine Vermutung von Paul Erdős. Sie sagt aus, dass eine Folge $a_1<a_2<a_3<\cdots$ natürlicher Zahlen mit der Eigenschaft

$\sum _{j=1}^{\mathrm{\infty }}\frac{1}{a_j}=\mathrm{\infty }$

bereits beliebig lange arithmetische Progressionen enthalten muss. Diese weit offene Vermutung würde zusammen mit dem Satz von Euler, $\sum _{p\text{Primzahl}}\frac{1}{p}=\mathrm{\infty }$, den Satz von Green-Tao implizieren.

Bereits der im 19. Jahrhundert bewiesene Dirichletsche Primzahlsatz kann über die Divergenz bestimmter unendlicher Reihen formuliert werden. Dirichlet konnte nachweisen, dass für teilerfremde $a\in \mathbb{Z}$ und $N\in \mathbb{N}$

$\sum _{\genfrac{}{}{0ex}{}{p\text{Primzahl}}{p\equiv a(\mathrm{mod}N)}}\frac{1}{p}=\mathrm{\infty },$

und verifizierte sogar das noch stärkere Resultat

$\underset{x\to 1^{+}}{\lim }\frac{\sum _{\genfrac{}{}{0ex}{}{p\text{Primzahl}}{p\equiv l_1(\mathrm{mod}N)}}\frac{1}{p^x}}{\sum _{\genfrac{}{}{0ex}{}{p\text{Primzahl}}{p\equiv l_2(\mathrm{mod}N)}}\frac{1}{p^x}}=1$

für zu $N$ teilerfremde $l_1$ und $l_2$. Trivialerweise implizieren diese Resultate die Aussage, dass es unendlich viele Primzahlen in der entsprechenden arithmetischen Progression $(a+kN{)}_{k\in \mathbb{Z}}$ gibt, wobei letzteres Resultat sogar auf eine Form der „Gleichverteilung“ hinweist.

Literatur (Auswahl)

• Herbert Amann, Joachim Escher: Analysis III. Zweite Auflage, Birkhäuser, Basel 2008, ISBN 978-3-7643-8883-6.
• Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Springer Spektrum, Berlin/Heidelberg 2022, ISBN 978-3-662-64388-4.
• Edwin F. Beckenbach, Richard Bellmann: Inequalities. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 30, Second Revised Printing, Springer-Verlag, Berlin / Heidelberg / New York 1965.
• Ludmila Bourchtein, Andrei Bourchtein: Theory of Infinite Sequences and Series. Birkhäuser, Cham 2022, ISBN 978-3-030-79430-9.
• Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer-Verlag, Berlin Heidelberg 1995, ISBN 3-540-58821-3.
• Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s (= Sources and Studies in the History of Mathematics and Physical Sciences.). Springer, New York (NY) 2008, ISBN 978-0-387-73467-5.
• Eberhard Freitag, Rolf Busam: Funktionentheorie 1. Springer-Verlag, 1993/ 4., korrigierte und erweiterte Auflage, Springer Spektrum, Berlin 2006, ISBN 3-540-31764-3.
• Izrail Solomonovic Gradshteyn, Iosif Mojseevic Ryzhik: Table of Integrals, Series and Products. Herausgegeben von Alan Jeffrey und Daniel Zwillinger. 7. Ausgabe. Elsevier Academic Press, Amsterdam u. a. 2007, ISBN 978-0-12-373637-6.
• Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Springer-Verlag, Berlin u. a. 1996, ISBN 3-540-59111-7 (Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 2).
• Jacob Korevaar: Tauberian Theory. A century of developments (= Grundlehren der mathematischen Wissenschaften.). Springer-Verlag, Berlin / Heidelberg / New York 2004, ISBN 3-540-21058-X.
• D. Mitrinovic: Analytic inequalities. Die Grundlehren der mathematischen Wissenschaften Band 165, Springer-Verlag, Berlin / Heidelberg / New York 1970, ISBN 978-3-642-99972-7.
• Anil Nerode, Noam Greenberg: Algebraic Curves and Riemann Surfaces for Undergraduates. Springer-Verlag, Switzerland 2022, ISBN 978-3-031-11615-5.
• Marius Overholt: A Course in Analytic Number Theory. (= Graduate Studies in Mathematics. Band 160). American Mathematical Society, Providence (R.I.) 2014, ISBN 978-1-4704-1706-2.
• Reinhold Remmert, Georg Schumacher: Funktionentheorie 1 (= Springer-Lehrbuch.). 5., neu bearbeitete Auflage, Springer-Verlag, Berlin/Heidelberg 2002, ISBN 3-540-41855-5.
• Thomas Sonar: 3000 Jahre Analysis. Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin 2016, ISBN 978-3-662-48917-8.
• Terence Tao: Analysis I (= Text and Readings in Mathematics.). Third Edition, Hindustan Book Agency, New Delhi 2006, ISBN 978-93-80250-64-9.
• Terence Tao: Analysis II (= Texts and readings in mathematics.). Third Edition, Hindustan Book Agency, New Delhi 2006, ISBN 978-93-80250-65-6.
• K. Zeller, W. Beekmann: Theorie der Limitierungsverfahren (= Ergebnisse der Mathematik und ihrer Grenzgebiete. Band 15). Springer-Verlag, Berlin / Heidelberg / New York 1970.
• Vorlage:Literatur