Differentialform

Der Begriff Differentialform (oft auch alternierende Differentialform genannt) geht auf den Mathematiker Élie Joseph Cartan zurück. Differentialformen sind ein grundlegendes Konzept der Differentialgeometrie. Sie erlauben eine koordinatenunabhängige Integration auf allgemeinen orientierten differenzierbaren Mannigfaltigkeiten.

Kontext

Es sei $U$

• eine offene Teilmenge des ${ℝ}^n$
• oder eine differenzierbare Untermannigfaltigkeit des ${ℝ}^n$
• oder eine differenzierbare Mannigfaltigkeit.

In jedem dieser Fälle gibt es

• den Begriff der differenzierbaren Funktion auf $U;$ der Raum der beliebig oft differenzierbaren Funktionen auf $U$ werde mit $C^{\mathrm{\infty }}(U)$ bezeichnet;
• den Begriff des Tangentialraums ${\mathrm{T}}_{p}U$ an $U$ in einem Punkt $p\in U;$
• den Begriff der Richtungsableitung $\frac{\partial f}{\partial X}$ für einen Tangentialvektor $X\in {\mathrm{T}}_{p}U$ und eine differenzierbare Funktion $f;$
• den Begriff des differenzierbaren Vektorfeldes auf $U;$ der Raum der Vektorfelder auf $U$ sei mit $\mathrm{\Gamma }(\mathrm{T}U)$ bezeichnet.

Der Dualraum des Tangentialraums ${\mathrm{T}}_{p}U$ wird als Kotangentialraum ${\mathrm{T}}_p^{*}U$ bezeichnet.

Definition

Differentialform

Eine Differentialform vom Grad $k$ auf $U$ oder kurz $k$-Form $\omega$ ist ein glatter Schnitt in der $k$-ten äußeren Potenz des Kotangentialbündels von $U$. In symbolischer Schreibweise bedeutet dies $\omega \in \mathrm{\Gamma }({\mathrm{\Lambda }}^k(T^{*}U))$, wobei $T^{*}U$ das Kotangentialbündel von $U$, ${\mathrm{\Lambda }}^k(T^{*}U)$ die $k$-te äußere Potenz von $T^{*}U$ und $\mathrm{\Gamma }({\mathrm{\Lambda }}^k(T^{*}U))$ somit die Menge der glatten Schnitte von ${\mathrm{\Lambda }}^k(T^{*}U)$ bezeichnet.

Dies bedeutet, dass jedem Punkt $p\in U$ eine alternierende Multilinearform ${\omega }_p$ auf dem Tangentialraum $T_{p}U$ zugeordnet wird, und zwar so, dass für $k$ glatte Vektorfelder $X_1,\dots ,X_k$ die Funktion

$p\mapsto {\omega }_p((X_1{)}_p,\dots ,(X_k{)}_p)\in ℝ$

glatt, also beliebig oft differenzierbar, ist.

Alternativ dazu kann man eine $k$-Form $\omega$ als eine alternierende, glatte multilineare Abbildung $\omega :(\mathrm{\Gamma }TU{)}^k\to C^{\mathrm{\infty }}(U)$ auffassen. Das bedeutet: $\omega$ ordnet $k$ Vektorfeldern $X_1,\dots ,X_k$ eine Funktion $\omega (X_1,\dots ,X_k)$ zu, sodass

• $\omega (X_1,\dots ,X{\text{'}}_i+X^{\prime }{\text{'}}_i,\dots ,X_k)=\omega (X_1,\dots ,X{\text{'}}_i,\dots ,X_k)+\omega (X_1,\dots ,X^{\prime }{\text{'}}_i,\dots ,X_k)$
• $\omega (X_1,\dots ,f\cdot X_i,\dots ,X_k)=f\cdot \omega (X_1,\dots ,X_i,\dots ,X_k)$ für $f\in C^{\mathrm{\infty }}(U),1\le i\le k$

und

• $\omega (X_1,\dots ,X_i,\dots ,X_j,\dots ,X_k)=-\omega (X_1,\dots ,X_j,\dots ,X_i,\dots ,X_k)$

gilt.

Alternative unter Rückgriff auf Tensorfelder: Eine $k$-Form ist ein alternierendes, kovariantes Tensorfeld der Stufe $k$.

Raum der Differentialformen

Die Menge der $k$-Formen auf $U$ bildet einen Vektorraum und wird mit ${\mathrm{\Omega }}^k(U)$ bezeichnet. Weiterhin setzt man

$\mathrm{\Omega }(U)=\underset{k=1}{\overset{\mathrm{\infty }}{⨁}}{\mathrm{\Omega }}^k(U).$

Für endlichdimensionale Mannigfaltigkeiten ist diese Summe endlich, da für $k>\dim U$ der Vektorraum ${\mathrm{\Omega }}^k(U)$ der Nullvektorraum ist. Die Menge $\mathrm{\Omega }(U)$ ist eine Algebra mit dem äußeren Produkt als Multiplikation und somit auch wieder ein Vektorraum. Aus topologischer Sicht ist dieser Raum auch eine Garbe.

Man kann ${\omega }_p$ als Element der äußeren Potenz ${\mathrm{\Lambda }}^k(T_p^{*}U)$ auffassen; infolgedessen definiert das äußere Produkt (d. h. das Produkt $\wedge$ in der äußeren Algebra) Abbildungen

${\mathrm{\Omega }}^k(U)\times {\mathrm{\Omega }}^{\ell }(U)\to {\mathrm{\Omega }}^{k+\ell }(U),(\omega ,\eta )\mapsto \omega \wedge \eta ,$

wobei $\omega \wedge \eta$ durch

$(\omega \wedge \eta {)}_p={\omega }_p\wedge {\eta }_p$

punktweise definiert ist.

Dieses Produkt ist graduiert-kommutativ, es gilt

$\omega \wedge \eta =(-1{)}^{\mathrm{deg}\omega \cdot \mathrm{deg}\eta }\cdot \eta \wedge \omega ;$

dabei bezeichnet $\mathrm{deg}\omega$ den Grad von $\omega ,$ d. h.: Ist $\omega$ eine $k$-Form, so ist $\mathrm{deg}\omega =k$. Demnach ist das Produkt zweier Formen ungeraden Grades antikommutativ und in allen anderen Kombinationen kommutativ.

Beispiele

• Glatte Funktionen sind 0-Formen.
• Pfaffsche Formen sind 1-Formen.

Koordinatendarstellung

Es sei $M$ eine $n$-dimensionale differenzierbare Mannigfaltigkeit. Weiter sei $(U,x)$ ein lokales Koordinatensystem (eine Karte). Dann ist

$B=\{\mathrm{d}{x}_{i_1}{|}_p\wedge \dots \wedge \mathrm{d}{x}_{i_k}{|}_p|i_1<\dots <i_k\}$

eine Basis von ${\mathrm{\Lambda }}^k(T_p^{*}M).$ Dabei ist $\mathrm{d}{x}_i$ das totale Differential der $i$-ten Koordinatenfunktion $x_i$. Das heißt, $\mathrm{d}{x}_i{|}_p$ ist diejenige Linearform auf $T_p(M)$, die den $i$-ten Basisvektor der Basis $\frac{\partial }{\partial x_1}{|}_p,\dots ,\frac{\partial }{\partial x_n}{|}_p$ auf 1 und alle anderen auf 0 abbildet.

Jede Differentialform $\omega \in {\mathrm{\Omega }}^k(M)$ hat auf jeder Karte $(U,x)$ eine eindeutige Darstellung

$\omega {|}_U=\sum _{1\le i_1<\dots <i_k\le n}{a}_{i_1,\dots ,i_k}\mathrm{d}{x}_{i_1}\wedge \dots \wedge \mathrm{d}{x}_{i_k}$

mit geeigneten differenzierbaren Funktionen $a_{i_1,\dots ,i_k}.$

Aus der Koordinatendarstellung ergibt sich, dass für $k>n$ die Nullform $\omega =0$ die einzige Differentialform ist.

Äußere Ableitung

Vorlage:Hauptartikel Die äußere Ableitung ist ein Operator, der einer $k$-Differentialform eine $(k+1)$-Differentialform zuordnet. Betrachtet man sie auf der Menge der $0$-Differentialformen, also auf der Menge der glatten Funktionen, so entspricht die äußere Ableitung der üblichen Ableitung für Funktionen.

Definition

Die äußere Ableitung $\mathrm{d}\omega$ einer $k$-Form $\omega$ wird induktiv mithilfe der Lie-Ableitung und der Cartan-Formel

${ℒ}_X=i_X\circ \mathrm{d}+\mathrm{d}\circ i_X$

definiert; dabei ist $X$ ein Vektorfeld, ${ℒ}_X$ die Lie-Ableitung und $i_X$ die Einsetzung von $X.$

Ist beispielsweise $\omega$ eine 1-Form, so ist

$({ℒ}_X\omega )(Y)={ℒ}_X(\omega (Y))-\omega ({ℒ}_X(Y))=X\omega (Y)-\omega ([X,Y])$

und

$((\mathrm{d}\circ i_X)\omega )(Y)=(\mathrm{d}(\omega (X)))(Y)=Y\omega (X),$

also

$\mathrm{d}\omega (X,Y)=X\omega (Y)-Y\omega (X)-\omega ([X,Y])$

für Vektorfelder $X,Y$; dabei bezeichnet $[X,Y]$ die Lie-Klammer.

Die allgemeine Formel lautet

$\begin{array}{ccc}\mathrm{d}\omega (X_0,\dots ,X_k)& =& \sum _{i=0}^k(-1{)}^i{X}_i\omega (X_0,\dots ,{\hat{X}}_i,\dots ,X_k)+\\ & & +\sum _{0\le i<j\le k}(-1{)}^{i+j}\omega ([X_i,X_j],X_0,\dots ,{\hat{X}}_i,\dots ,{\hat{X}}_j,\dots ,X_k);\end{array}$

dabei bedeutet das Dach $\stackrel{}{^}$ im Zeichen ${\hat{X}}_i$, dass das entsprechende Argument wegzulassen ist.

Eigenschaften

Die äußere Ableitung hat folgende Eigenschaften:

• Die äußere Ableitung ist eine Antiderivation. Das heißt, $\mathrm{d}$ ist $ℝ$-linear, und für $\alpha \in {\mathrm{\Omega }}^k(U),\beta \in {\mathrm{\Omega }}^l(U)$ gilt die Leibnizregel

$\mathrm{d}(\alpha \wedge \beta )=\mathrm{d}\alpha \wedge \beta +(-1{)}^k\alpha \wedge \mathrm{d}\beta .$

• Sei $f\in C^{\mathrm{\infty }}(U),$ dann stimmt die äußere Ableitung mit dem totalen Differential überein.
• ${\mathrm{d}}^2=\mathrm{d}\circ \mathrm{d}=0$
• Die äußere Ableitung respektiert Einschränkungen. Es sei also $U\subset V\subset M$ offen und $\alpha \in {\mathrm{\Omega }}^k(V).$ Dann gilt $\mathrm{d}(\alpha {|}_U)=(\mathrm{d}\alpha ){|}_U.$ Man nennt die äußere Ableitung deshalb auch einen lokalen Operator.

Diese vier Eigenschaften charakterisieren die äußere Ableitung vollständig. Das heißt, man kann aus diesen Eigenschaften die obige Summenformel herleiten. Rechnet man mit der äußeren Ableitung, so bevorzugt man das Rechnen mit den Eigenschaften der Ableitung und vermeidet die obige Formel.

Koordinatendarstellung der äußeren Ableitung

Die äußere Ableitung einer Differentialform

$\omega =\sum _{1\le i_1<\dots <i_k\le n}{a}_{i_1,\dots ,i_k}(x)\cdot \mathrm{d}{x}_{i_1}\wedge \dots \wedge \mathrm{d}{x}_{i_k}$

in Koordinatendarstellung lautet

$\mathrm{d}\omega =\sum _{1\le i_1<\dots <i_k\le n}\mathrm{d}{a}_{i_1,\dots ,i_k}\wedge \mathrm{d}{x}_{i_1}\wedge \dots \wedge \mathrm{d}{x}_{i_k}$

mit den totalen Differentialen der Koeffizientenfunktionen

$\mathrm{d}{a}_{i_1,\dots ,i_k}=\sum _{j=1}^n\frac{\partial a_{i_1,\dots ,i_k}}{\partial x_j}\mathrm{d}{x}_j$.

Um die dabei entstehenden Ausdrücke wieder durch die Standardbasis auszudrücken, sind die Identitäten

$\mathrm{d}{x}_i\wedge \mathrm{d}{x}_j=-\mathrm{d}{x}_j\wedge \mathrm{d}{x}_i$

und

$\mathrm{d}{x}_i\wedge \mathrm{d}{x}_i=0$

wichtig.

Beispiel

Für $n=2,k=1$ gilt

$\begin{array}{cc}\mathrm{d}(a_1\cdot \mathrm{d}{x}_1+a_2\cdot \mathrm{d}{x}_2)& =\mathrm{d}{a}_1\wedge \mathrm{d}{x}_1+\mathrm{d}{a}_2\wedge \mathrm{d}{x}_2\\ & =(\frac{\partial a_1}{\partial x_1}\mathrm{d}{x}_1+\frac{\partial a_1}{\partial x_2}\mathrm{d}{x}_2)\wedge \mathrm{d}{x}_1+(\frac{\partial a_2}{\partial x_1}\mathrm{d}{x}_1+\frac{\partial a_2}{\partial x_2}\mathrm{d}{x}_2)\wedge \mathrm{d}{x}_2\\ & =\frac{\partial a_1}{\partial x_1}\cdot \mathrm{d}{x}_1\wedge \mathrm{d}{x}_1+\frac{\partial a_1}{\partial x_2}\cdot \mathrm{d}{x}_2\wedge \mathrm{d}{x}_1+\frac{\partial a_2}{\partial x_1}\cdot \mathrm{d}{x}_1\wedge \mathrm{d}{x}_2+\frac{\partial a_2}{\partial x_2}\cdot \mathrm{d}{x}_2\wedge \mathrm{d}{x}_2\\ & =(\frac{\partial a_2}{\partial x_1}-\frac{\partial a_1}{\partial x_2})\cdot \mathrm{d}{x}_1\wedge \mathrm{d}{x}_2.\end{array}$

Allgemein gilt für die äußere Ableitung einer 1-Form

$\mathrm{d}(\sum _{i=1}^n{a}_i\cdot \mathrm{d}{x}_i)=\sum _{1\le i<j\le n}(\frac{\partial a_j}{\partial x_i}-\frac{\partial a_i}{\partial x_j})\cdot \mathrm{d}{x}_i\wedge \mathrm{d}{x}_j$

Für $n=3$ bilden also die Koeffizienten der äußeren Ableitung einer 1-Form die Rotation des aus den Koeffizienten der 1-Form gebildeten Vektors.

Weitere Operationen auf Differentialformen

Inneres Produkt

Sei $X\in T(M)$ ein glattes Vektorfeld. Das innere Produkt ist eine lineare Abbildung

$i_X:{\mathrm{\Omega }}^k(M)\to {\mathrm{\Omega }}^{k-1}(M),$

die durch

$\omega \mapsto \omega (X,\cdot ,\dots ,\cdot )$

gegeben ist. Das heißt, das innere Produkt bildet eine $k$-Form $\omega$ auf eine $(k-1)$-Form ab, indem die Form an einem festen Vektorfeld $X$ ausgewertet wird. Diese Abbildung ist ein Analogon der Tensorverjüngung auf dem Raum der Differentialformen. Deshalb wird diese Operation im Englischen auch manchmal „contraction“ genannt.

Das innere Produkt $i_X$ ist eine Antiderivation. Das heißt, für $\omega \in {\mathrm{\Omega }}^k(M)$ und $\nu \in {\mathrm{\Omega }}^l(M)$ gilt die Leibnizregel

$i_X(\omega \wedge \nu )=(i_X\omega )\wedge \nu +(-1{)}^k\omega \wedge (i_X\nu ).$

Außerdem gilt für das innere Produkt $i_X\circ i_X=0.$

Rücktransport (Pullback) von Differentialformen

Schema eines Pull-Back, $T^{*}M$ ist das Kotangentialbündel der Mannigfaltigkeit $M$ und entsprechend für $N$

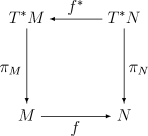
Ist $f:M\to N$ eine glatte Abbildung zwischen differenzierbaren Mannigfaltigkeiten, so ist für $\omega \in {\mathrm{\Omega }}^k(N)$ die mittels $f$ zurückgeholte Form $(f^{*}\omega )\in {\mathrm{\Omega }}^k(M)$ wie folgt definiert:

$(f^{*}\omega )(X_1,\dots ,X_k):=\omega (\mathrm{d}f(X_1),\dots ,\mathrm{d}f(X_k))$

Dabei ist $df:TM\to TN$ die durch $f$ induzierte Abbildung der Ableitungen, auch „push-forward“ genannt. Das Zurückziehen ist mit der äußeren Ableitung und dem äußeren Produkt verträglich:

• $f^{*}(\mathrm{d}\omega )=\mathrm{d}(f^{*}\omega )$

(ausführlicher geschrieben: auf der linken Seite $\mathrm{d}={\mathrm{d}}^{(N)}$, auf der rechten Seite dagegen $\mathrm{d}={\mathrm{d}}^{(M)}$) und

• $f^{*}(\omega \wedge \eta )=(f^{*}\omega )\wedge (f^{*}\eta )$

für alle $\omega ,\eta \in {\mathrm{\Omega }}^{\text{pback}}(N)$

Insbesondere induziert $f$ eine Abbildung zwischen den De-Rham-Kohomologie-Gruppen (siehe unten)

$f^{\text{pback}}:{\mathrm{H}}_{\text{dR}}^k(N)⟶{\mathrm{H}}_{\text{dR}}^k(M),$

wobei die Umkehr der Pfeilrichtung gegenüber $f:M\to N$ zu beachten ist („pull-back“, „Kohomologie“ statt „Homologie“).

Duale Form und Stern-Operator

Vorlage:Hauptartikel Betrachtet werden äußere Formen in einem $n$-dimensionalen Raum, in dem ein inneres Produkt (Metrik) definiert ist, sodass eine orthonormale Basis $e_i$ des Raumes gebildet werden kann. Die zu einer äußeren Form von Grad $k$ in diesem $n$-dimensionalen Raum duale Form ist eine $(n-k)$-Form

$*(e_1\wedge e_2\wedge \dots \wedge e_k)=e_{k+1}\wedge e_{k+2}\wedge \dots \wedge e_n.$

Dabei seien beide Seiten in orientierter Form geschrieben. Formal wird die duale Form durch Anwendung des (Hodge-)$*$-Operators bezeichnet. Speziell für Differentialformen im dreidimensionalen euklidischen Raum ergibt sich:

$*\mathrm{d}x=\mathrm{d}y\wedge \mathrm{d}z$

$*\mathrm{d}y=\mathrm{d}z\wedge \mathrm{d}x$

$*\mathrm{d}z=\mathrm{d}x\wedge \mathrm{d}y$

mit den 1-Formen $dx,dy,dz$. Dabei wurde berücksichtigt, dass die orientierte Reihenfolge hier $(y,z),(z,x)$ und $(x,y)$ ist (zyklische Vertauschungen in $(x,y,z)$).

Das $*$-Symbol soll die Tatsache unterstreichen, dass damit ein inneres Produkt im Raum der Formen auf einem zugrundeliegenden Raum $M$ gegeben ist, denn $\alpha \wedge *\beta$ lässt sich für zwei $k$-Formen $\alpha$ und $\beta$ als Volumenform schreiben und das Integral

$(\alpha ,\beta )=\underset{M}{\int }\alpha \wedge *\beta$

liefert eine reelle Zahl. Der Zusatz dual zeigt an, dass die zweifache Anwendung auf eine $k$-Form wieder die $k$-Form ergibt – bis auf das Vorzeichen, das gesondert betrachtet werden muss. Genauer gilt für eine $k$-Form in einem $n$-dimensionalen Raum, dessen Metrik die Signatur $s$ hat ($s=+1$ im euklidischen Raum, $s=-1$ im Minkowski-Raum):

$**\alpha =(-1{)}^{k(n-k)}s\alpha$

Oben wurde gezeigt, wie sich im 3-dimensionalen euklidischen Raum bei äußerer Ableitung einer 1-Form $\alpha$ die 2-Form $d\wedge \alpha$ ergibt mit den Komponenten des Rotations-Vektors der Vektoranalysis als Koeffizienten. Diese 2-Form kann man mit Hilfe des $*$-Operators nun auch formal direkt als 1-Form (rot-Vektor) schreiben: $*(d\wedge \alpha )$. Analog wird der $*$-Operator zur „Übersetzung“ des oben formulierten Satzes von Stokes in die Vektoranalysis-Form benutzt.

De-Rham-Kohomologie

Vorlage:Hauptartikel Aus der graduierten Algebra $\mathrm{\Omega }(U)$ kann zusammen mit der äußeren Ableitung ein Kokettenkomplex konstruiert werden. Aus diesem wird dann mit den üblichen Methoden der homologischen Algebra eine Kohomologie definiert. Georges de Rham konnte zeigen, dass diese nach ihm benannte Kohomologietheorie mit der singulären Kohomologie übereinstimmt. Um die De-Rham-Kohomologie zu definieren, werden zuerst die Begriffe der exakten und der geschlossenen Differentialform definiert:

Exakte und geschlossene Formen

Eine $k$-Form $\omega$ heißt geschlossen, wenn $\mathrm{d}\omega =0$ gilt; sie heißt exakt, wenn es eine $(k-1)$-Form $\eta$ gibt, sodass $\omega =\mathrm{d}\eta$ gilt. Aufgrund der Formel $\mathrm{d}\mathrm{d}\eta =0$ ist jede exakte Form geschlossen. Man beachte, dass Geschlossenheit im Gegensatz zu Exaktheit eine lokale Eigenschaft ist: Ist $\{V_{\alpha }\}$ eine offene Überdeckung von $U,$ so ist eine $k$-Form $\omega$ genau dann geschlossen, wenn die Einschränkung von $\omega$ auf $V_{\alpha }$ für jedes $\alpha$ geschlossen ist.

Die De-Rham-Kohomologiegruppen

Der Faktorraum

(Menge aller geschlossenen $k$-Formen auf $U$) $/$ (Menge aller exakten $k$-Formen auf $U$)

heißt $k$-te De-Rham-Kohomologiegruppe ${\mathrm{H}}_{\mathrm{d}\mathrm{R}}^k(U).$ Sie enthält Informationen über die globale topologische Struktur von $U.$

Das Lemma von Poincaré

Vorlage:Hauptartikel Das Lemma von Poincaré besagt, dass ${\mathrm{H}}_{\mathrm{d}\mathrm{R}}^k(U)=0$ gilt für $k>0$ und Sterngebiete $U$. Allgemeiner gilt die Aussage dieses Lemmas für zusammenziehbare offene Teilmengen $U$ des ${ℝ}^n.$ Der Beweis ist konstruktiv, d. h., es werden explizite Beispiele konstruiert, was für Anwendungen sehr wichtig ist. Man beachte, dass ${\mathrm{H}}_{\mathrm{d}\mathrm{R}}^0(U)$ aus den lokal konstanten Funktionen besteht, da es per definitionem keine exakten 0-Formen gibt. Es ist also ${\mathrm{H}}_{\mathrm{d}\mathrm{R}}^0(U)=0$ für jedes $U\ne \varnothing .$

Ist $\omega$ geschlossen und $\eta =\mathrm{d}{\eta }^{\prime }$ exakt, so folgt

$\omega \wedge \eta =\omega \wedge \mathrm{d}{\eta }^{\prime }=(-1{)}^{\mathrm{deg}\omega }\mathrm{d}(\omega \wedge {\eta }^{\prime }).$

Entsprechendes gilt, falls $\omega$ exakt und $\eta$ geschlossen ist. Damit gibt es induzierte Abbildungen

${\mathrm{H}}_{\mathrm{d}\mathrm{R}}^k(U)\times H_{\mathrm{d}\mathrm{R}}^m(U)⟶{\mathrm{H}}_{\mathrm{d}\mathrm{R}}^{k+m}(U).$

Ein Beispiel aus der Elektrodynamik

In der Elektrodynamik impliziert das Lemma von Poincaré, dass zu jedem Paar $\overrightarrow{E},\overrightarrow{B}$ elektromagnetischer Felder, die zu einer zweistufigen alternierenden Differentialform $𝐅$ in einem vierdimensionalen Minkowskiraum zusammengefasst werden können, eine einstufige Vektorpotentialform $𝐀$ mit $𝐅=\mathrm{d}𝐀$ existiert, ein sogenanntes „Viererpotential“, siehe auch Vierervektor. Auch Strom- und Ladungsdichten können zu einem Vierervektor bzw. zu einer entsprechenden 3-Form $𝐣$ zusammengefasst werden.

Die relativistischen Maxwell-Gleichungen der Elektrodynamik auf einer vierdimensionalen Raum-Zeit-Mannigfaltigkeit $M$ (mit Metrik $g_{\alpha ,\beta }$ und Determinante der Metrik $g$, wobei hier natürlich die Signatur eines Minkowski-Raumes vorliegt, etwa $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(+1,-1,-1,-1)$ für $\alpha =0,1,2,3,$ entsprechend der Definition des Linienelements $\mathrm{d}s$) lauten beispielsweise unter Verwendung dieser Symbolik:

$\mathrm{d}𝐅=2({\partial }_{\gamma }{F}_{\alpha \beta }+{\partial }_{\beta }{F}_{\gamma \alpha }+{\partial }_{\alpha }{F}_{\beta \gamma })\mathrm{d}{x}^{\alpha }\wedge \mathrm{d}{x}^{\beta }\wedge \mathrm{d}{x}^{\gamma }=0$

(die sogenannte Bianchi-Identität) und

$\mathrm{d}(*𝐅)={F^{\alpha \beta }}_{;\alpha }\sqrt{-g}{ϵ}_{\beta \gamma \delta \eta }\mathrm{d}{x}^{\gamma }\wedge \mathrm{d}{x}^{\delta }\wedge \mathrm{d}{x}^{\eta }=𝐣$

mit dem elektromagnetischen Feldtensor ausgedrückt als 2-Form

$𝐅=F_{\alpha \beta }\mathrm{d}{x}^{\alpha }\wedge \mathrm{d}{x}^{\beta },$

z. B. $F_{1,2}=B_z$ mit der $z$-Komponente des Vektors der magnetischen Induktion, und mit dem Strom (geschrieben als 3-Form)

$𝐣=j^{\alpha }\sqrt{-g}{ϵ}_{\alpha \beta \gamma \delta }\mathrm{d}{x}^{\beta }\wedge \mathrm{d}{x}^{\gamma }\wedge \mathrm{d}{x}^{\delta }.$

Hierbei ist ${ϵ}_{\alpha \beta \gamma \delta }$ das Antisymmetrisierungssymbol (Levi-Civita-Symbol) und das Semikolon steht für die kovariante Ableitung. Wie üblich wird über doppelt vorkommende Indizes summiert (Einsteinsche Summenkonvention) und es werden natürliche Einheiten verwendet (Lichtgeschwindigkeit $c$ ersetzt durch $1$). Durch Anwendung des $*$-Operators kann man den zweiten Satz der vier Maxwellgleichungen auch alternativ mit einer 1-Form für den Strom schreiben. Aus den Maxwellgleichungen sieht man, dass $𝐅$ und $*𝐅$ in der Elektrodynamik ganz unterschiedlichen Gleichungen gehorchen, die Dualität also keine Symmetrie dieser Theorie ist. Das liegt daran, dass die Dualität elektrische und magnetische Felder vertauscht, in der Elektrodynamik aber keine magnetischen Monopole bekannt sind. Die freien Maxwellgleichungen, die sich für $𝐣\equiv 0$ ergeben, haben dagegen duale Symmetrie.

Die Potentialform $𝐀$ ist nur bis auf einen additiven Zusatz $\mathrm{d}\chi$ eindeutig: $𝐀$ und $𝐀+\mathrm{d}\chi$ ergeben dasselbe $𝐅$, mit einer Eichform $\chi$, die $\mathrm{d}(\mathrm{d}\chi )\equiv 0$ erfüllt, aber ansonsten willkürlich ist. Man kann diese zusätzliche sogenannte Eichfreiheit benutzen, um punktweise zusätzliche Nebenbedingungen zu erfüllen. In der Elektrodynamik fordert man beispielsweise, dass für $𝐀$ überall die zusätzliche sogenannte Lorenz-Bedingung (Lorenz-Eichung) $\mathrm{d}(*𝐀)=0$ gelten soll, in den vier Komponenten lautet diese Bedingung einfach ${\partial }_{\nu }{A}^{\nu }=0$. Durch diese „Eichfixierung“ ergibt sich schließlich als eindeutige Lösung aller vier Maxwell-Gleichungen das sogenannte „retardierte Potential“:

$A^{\nu }(𝐫,t)=\int \frac{j^{\nu }({𝐫}^{\prime },t-\frac{|𝐫-{𝐫}^{\prime }|}{c})}{4\pi |𝐫-{𝐫}^{\prime }|}{\mathrm{d}}^3{r}^{\prime }$

Beim Übergang zum Dualen ist zu beachten, dass man es nicht mit dem ${ℝ}^4$, sondern mit ${𝕄}^4$ zu tun hat, der eine andere Metrik, nämlich die Minkowski-Metrik, trägt. Das bei Lorentztransformationen invariante Linienelement ist $\mathrm{d}{s}^2=-c^2\mathrm{d}{\tau }^2=\mathrm{d}{x}^2+\mathrm{d}{y}^2+\mathrm{d}{z}^2-c^2\mathrm{d}{t}^2=-\mathrm{d}{x}_{\nu }\mathrm{d}{x}^{\nu }$, wobei $\mathrm{d}\tau$ das Differential der Eigenzeit ist und die Summenkonvention verwendet wurde. Ko- und kontravariante Vierervektorkomponenten unterscheiden sich nun. Zwar ist $+\mathrm{d}{x}_0\equiv +\mathrm{d}{x}^0=c\mathrm{d}t$, aber $-\mathrm{d}{x}_1\equiv +\mathrm{d}{x}^1=\mathrm{d}x$, $-\mathrm{d}{x}_2\equiv +\mathrm{d}{x}^2=\mathrm{d}y$ und $-\mathrm{d}{x}_3\equiv +\mathrm{d}{x}^3=\mathrm{d}z$.

Integrationstheorie

Orientierung

Vorlage:Hauptartikel Ist $n=\dim U,$ so heißt eine $n$-Form auf $U,$ die in keinem Punkt verschwindet, eine Orientierung auf $U.$ $U$ zusammen mit einer derartigen Form heißt orientiert. Eine Orientierung $\alpha$ definiert Orientierungen der Tangential- und Kotangentialräume: Eine Basis ${\eta }_1,\dots ,{\eta }_n$ des Kotangentialraums in einem Punkt $p$ sei positiv orientiert, wenn

${\alpha }_p=a\cdot {\eta }_1\wedge \dots \wedge {\eta }_n$

mit einer positiven Zahl $a$ gilt. Eine Basis $X_1,\dots ,X_n$ des Tangentialraums in einem Punkt $p$ sei positiv orientiert, wenn

$\alpha (X_1,\dots ,X_n)>0$

gilt.

Zwei Orientierungen heißen äquivalent, wenn sie sich nur um einen überall positiven Faktor unterscheiden; diese Bedingung ist äquivalent dazu, dass sie auf jedem Tangential- oder Kotangentialraum dieselbe Orientierung definieren.

Ist $U$ zusammenhängend, so gibt es entweder gar keine oder genau zwei Äquivalenzklassen.

$U$ heißt orientierbar, wenn eine Orientierung von $U$ existiert.

Integration von Differentialformen

Es sei wieder $n=\dim U,$ und wir nehmen an, auf $U$ sei eine Orientierung gewählt. Dann gibt es ein kanonisches Integral

$\underset{U}{\int }\omega$

für $n$-Formen $\omega .$ Ist $U$ eine offene Teilmenge des ${ℝ}^n$, sind $x_1,\dots ,x_n$ die Standardkoordinatenfunktionen im ${ℝ}^n$ und ist

$\omega =f\mathrm{d}{x}_1\wedge \dots \wedge \mathrm{d}{x}_n,$

so gilt:

$\underset{U}{\int }\omega =\underset{U}{\int }f(x_1,\dots ,x_n)\mathrm{d}{x}_1\dots \mathrm{d}{x}_n$

Das Integral auf der rechten Seite ist das gewöhnliche Lebesgue-Integral im ${ℝ}^n.$

Ist $M$ eine $n$-dimensionale orientierte Mannigfaltigkeit, $U\subset M$ offen und $\varphi :U\to {ℝ}^n$ eine Karte, so definiert man

$\underset{U}{\int }\omega =\underset{\varphi (U)}{\int }({\varphi }^{-1}{)}^{*}\omega$

als Integral der $n$-Form $\omega$ über ein Kartengebiet $U$. Die Differentialform $\omega$ wird also mit der Parametrisierung ${\varphi }^{-1}:\varphi (U)\to U$ von $U$ auf die offene Teilmenge $\varphi (U)\subset {ℝ}^n$ zurückgeholt und dann nach obiger Definition integriert. Aus dem Transformationssatz folgt, dass diese Definition invariant gegenüber Koordinatenwechsel ist.

Ist allgemeiner $B$ eine messbare Teilmenge von $U$, so definiert man

$\underset{B}{\int }\omega =\underset{U}{\int }{\chi }_B\omega$

mit der charakteristischen Funktion ${\chi }_B$, d. h., $\omega$ wird außerhalb von $B$ null gesetzt.

Zur Definition des Integrals über ganz $M$ kann eine Zerlegung

$M=\bigcup _{j=1}^{\mathrm{\infty }}{M}_j$

in abzählbar viele paarweise disjunkte messbare Teilmengen $M_j$ gewählt werden, sodass jedes $M_j$ ganz in einem Kartengebiet $U_j$ enthalten ist. Damit setzt man

$\underset{M}{\int }\omega =\sum _{j=1}^{\mathrm{\infty }}\underset{M_j}{\int }\omega$.

Für Integrale von Differentialformen gilt der folgende Transformationssatz: Ist $f:M\to N$ ein orientierungserhaltender Diffeomorphismus, dann gilt für $\omega \in {\mathrm{\Omega }}^n(N)$

$\underset{N}{\int }\omega =\underset{M}{\int }{f}^{*}\omega$

mit der auf $M$ zurückgeholten Form $f^{*}\omega$.

Satz von Stokes

Vorlage:Hauptartikel Ist $M$ eine kompakte orientierte $n$-dimensionale differenzierbare Mannigfaltigkeit mit Rand $\partial M$ und versieht man $\partial M$ mit der induzierten Orientierung, so gilt für jede $(n-1)$-Form $\omega$

$\underset{M}{\int }\mathrm{d}\omega =\underset{\partial M}{\int }\omega .$

Dieser Satz ist eine weitreichende Verallgemeinerung des Hauptsatzes der Differential- und Integralrechnung. Er enthält als Spezialfälle den gaußschen Integralsatz und den klassischen Integralsatz von Stokes.

Ist $M$ geschlossen, das heißt, gilt $\partial M=\mathrm{\varnothing },$ so folgt für jede exakte $n$-Form ${\omega }^{\text{exakt}},$ d. h. für $\omega \equiv {\omega }^{\text{exakt}}=\mathrm{d}\phi ,$ die Beziehung

$\underset{M}{\int }{\omega }^{\text{exakt}}=\underset{M}{\int }\mathrm{d}\phi =\underset{\partial M=\mathrm{\varnothing }}{\int }\phi =0.$

Zur Verdeutlichung der genannten Eigenschaft von $M$ benutzt man oft die Formulierung mit einem Kreis-Integral:

${\oint }_M{\omega }^{\text{exakt}}=0$

Das Integral liefert eine Abbildung

${\mathrm{H}}_{\mathrm{d}\mathrm{R}}^n(M)\to ℝ.$

Ist $M$ zusammenhängend, so ist diese Abbildung ein Isomorphismus. Man kommt damit zur De-Rham-Kohomologie zurück (s. o.).

Rechenbeispiele

Auf ${ℝ}^3$ mit den kartesischen Koordinaten $(x,y,z)$ seien die 1-Form

$\omega =z^2\mathrm{d}x+2y\mathrm{d}y+xz\mathrm{d}z$

und die 2-Form

$\nu =z\mathrm{d}z\wedge \mathrm{d}x$

gegeben.

Für das äußere Produkt gilt:

$\omega \wedge \nu =z^3\underset{=0}{\underbrace{\mathrm{d}x\wedge \mathrm{d}z\wedge \mathrm{d}x}}+2yz\underset{=\mathrm{d}x\wedge \mathrm{d}y\wedge \mathrm{d}z}{\underbrace{\mathrm{d}y\wedge \mathrm{d}z\wedge \mathrm{d}x}}+x{z}^2\underset{=0}{\underbrace{\mathrm{d}z\wedge \mathrm{d}z\wedge \mathrm{d}x}}=2yz\mathrm{d}x\wedge \mathrm{d}y\wedge \mathrm{d}z$

Die äußere Ableitung von $\omega$ ergibt

$\mathrm{d}\omega =2z\mathrm{d}z\wedge \mathrm{d}x+2\mathrm{d}y\wedge \mathrm{d}y+(z\mathrm{d}x+x\mathrm{d}z)\wedge \mathrm{d}z=2z\mathrm{d}z\wedge \mathrm{d}x-z\mathrm{d}z\wedge \mathrm{d}x=z\mathrm{d}z\wedge \mathrm{d}x$,

also $\mathrm{d}\omega =\nu$. Insbesondere ist $\nu$ exakt und folglich geschlossen, d. h. $\mathrm{d}\nu =0$. Das lässt sich auch durch direkte Rechnung überprüfen: $\mathrm{d}\nu =\mathrm{d}z\wedge \mathrm{d}z\wedge \mathrm{d}x=0$.

Sei weiter $c:[0,1]\to {ℝ}^3$ gegeben durch $c(t)=(t^2,2t,1)$, dann folgt mit $x=t^2$, $y=2t$, $z=1$ und $\mathrm{d}x=2t\mathrm{d}t$, $\mathrm{d}y=2\mathrm{d}t$, $\mathrm{d}z=0$ für die auf $[0,1]$ zurückgeholte Form:

$c^{*}\omega =2t\mathrm{d}t+8t\mathrm{d}t=10t\mathrm{d}t$

Für das Integral von $\omega$ über die durch $c$ gegebene Kurve $\mathrm{\Gamma }=c([0,1])$ im ${ℝ}^3$ ergibt sich somit

$\underset{\mathrm{\Gamma }}{\int }\omega =\underset{[0,1]}{\int }{c}^{*}\omega =\underset{0}{\overset{1}{\int }}10t\mathrm{d}t=5$.

Ist $S^2=\{𝐱\in {ℝ}^3|\Vert 𝐱{\Vert }_2=1\}$ die Einheitssphäre im ${ℝ}^3$, so ist $S^2$ der Rand der Einheitskugel $B^3=\{𝐱\in {ℝ}^3|\Vert 𝐱{\Vert }_2<1\}$, also $S^2=\partial B^3$. Nach dem Satz von Stokes gilt also wegen $\mathrm{d}\nu =0$

$\underset{S^2}{\int }\nu =\underset{B^3}{\int }\mathrm{d}\nu =0$.

Die 3-Form $\omega \wedge \nu$ kann beispielsweise über den Einheitswürfel $W=[0,1{]}^3$ integriert werden. Ihr Integral stimmt mit dem Lebesgue-Integral der Koeffizientenfunktion $(x,y,z)\mapsto 2yz$ überein:

$\underset{W}{\int }\omega \wedge \nu =\underset{W}{\int }2yz\mathrm{d}x\wedge \mathrm{d}y\wedge \mathrm{d}z=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}2yz\mathrm{d}x\mathrm{d}y\mathrm{d}z=2\cdot \underset{0}{\overset{1}{\int }}y\mathrm{d}y\cdot \underset{0}{\overset{1}{\int }}z\mathrm{d}z=\frac{1}{2}$.

Komplexe Differentialformen

Vorlage:Hauptartikel In der Theorie der komplexen Differentialformen wird der hier eingeführte Kalkül auf komplexe Mannigfaltigkeiten übertragen. Dies funktioniert größtenteils analog zur Definition der hier beschriebenen Formen. Jedoch werden hier analog zu den komplexen Zahlen die Räume der komplexen Differentialformen in zwei Räume (reeller) Differentialformen

${ℰ}^r(M)\cong {\mathrm{\Omega }}^{r,r}(M)={\mathrm{\Omega }}^r(M)\oplus i{\mathrm{\Omega }}^r(M)$

zerlegt. Der Raum ${\mathrm{\Omega }}^{p,q}$ heißt dann der Raum der $(p,q)$-Formen. Auf diesen Räumen kann man analog zur äußeren Ableitung zwei neue Ableitungen definieren. Diese werden Dolbeault- und Dolbeault-Quer-Operator genannt, und analog zur De-Rham-Kohomologie kann man mit Hilfe des Dolbeault-Quer-Operators wieder eine Kohomologie bilden. Diese heißt Dolbeault-Kohomologie.

Siehe auch

• Vektorwertige Differentialformen

Literatur

• Herbert Amann, Joachim Escher: Analysis III. 2. Auflage. Birkhäuser, Basel 2008, ISBN 978-3-7643-8883-6, Kapitel XI und XII.
• Henri Cartan: Differentialformen. Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01443-1.
• Klaus Jänich: Vektoranalysis. 5. Auflage. Springer, Berlin / Heidelberg 2005, ISBN 978-3-540-27338-7.
• Shigeyuki Morita: Geometry of differential forms. American Mathematical Society, 2001, ISBN 0821810456.
• Harley Flanders: Differential forms with applications to the physical sciences. Academic Press, 1963.
• Harold Edwards: Advanced Calculus – a differential forms approach. Birkhäuser, 1994 (zuerst 1969).
• Steven H. Weintraub: Differential Forms – a complement to vector calculus. Academic Press, 1997.

Weblinks

• Gunnar Fløystad: The Exterior Algebra and Central Notions in Mathematics (PDF; 182 kB). Notices AMS, Band 62, 2015, Nr. 4.
• Differential Form in nLab.