2-Brücken-Knoten

In der Knotentheorie, einem Teilgebiet der Mathematik, sind 2-Brücken-Knoten bzw. 2-Brücken-Verschlingungen (auch: Knoten bzw. Verschlingungen mit 2 Brücken) eine Klasse von Knoten bzw. Verschlingungen. Sie wurden unter dem Namen Viergeflechte 1956 von Horst Schubert klassifiziert. Weil sie durch eine rationale Zahl $\frac{p}{q}$ klassifiziert werden können, werden sie häufig auch als rationale Knoten bzw. rationale Verschlingungen bezeichnet.

Definition

Ein 2-Brūckenknoten ist ein Knoten $K$, dessen Brückenzahl

$br(K)=2$

ist. Das bedeutet, dass er sich so in $4$ Intervalle zerlegen lässt, dass für eine geeignete Ebene $E\subset {ℝ}^3$ jeweils $2$ Intervalle in beiden von der Ebene berandeten Halbräumen liegen. (Äquivalent kann man auch verlangen, dass $2$ Intervalle in einer Ebene und die anderen beiden Intervalle in einem der berandeten Halbräume liegen.)

Analog definiert man eine Verschlingung mit 2 Brücken als eine Verschlingung $L$ mit Brückenzahl $br(L)=2$.

Eine äquivalente Definition besagt, dass der Knoten bzw. die Verschlingung nach einer geeigneten Isotopie genau 2 Maxima bzgl. einer Höhenfunktion $h:S^3\to ℝ$ hat.

Conway-Normalform

Schematische Darstellung einer 2-Brücken-Verschlingung

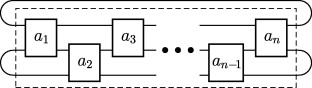
Aus der unten stehenden Klassifikation ergibt sich, dass man jede Verschlingung mit 2 Brücken wie im Bild rechts darstellen kann, wobei $a_i\in \mathbb{Z}$ die Anzahl der Halbtwists in der jeweiligen Box bezeichnet und für gerade bzw. ungerade $i$ positive $a_i$ links- bzw. rechtshändigen Halbtwists entsprechen.

Diese Darstellung wird als Conway-Normalform bezeichnet.

Man kann stets erreichen, dass alle $a_i$ dasselbe Vorzeichen haben. Insbesondere gibt die Conway-Normalform dann ein alternierendes Knotendiagramm.

Klassifikation

Die über einer 2-Brücken-Verschlingung verzweigte 2-fache Überlagerung der 3-Sphäre ist ein Linsenraum $L(p,q)$. Die 2-Brücken-Verschlingungen werden durch diese Linsenräume klassifiziert. Man bezeichnet deshalb mit $K(p,q)$ diejenige Verschlingung, für die man den Linsenraum $L(p,q)$ erhält.

Insbesondere entsprechen zwei rationale Zahlen $\frac{p_1}{q_1}$ und $\frac{p_2}{q_2}$ genau dann isotopen Verschlingungen, wenn

$p_1=p_2$ und entweder $q_1\equiv q_{2}modp$ oder $q_1{q}_2\equiv 1modp$ ist.

Modulo dieser Identitäten werden 2-Brücken-Verschlingungen also durch eine rationale Zahl $\frac{p}{q}$ klassifiziert, wobei man $p>0$ und $-p<q<p$ annehmen kann.

In der oben beschriebenen Conway-Normalform entspricht $\frac{p}{q}$ dem Kettenbruch $[a_0;a_1,a_2,a_3,\dots ]$:

$\frac{p}{q}=\frac{1}{a_1+\frac{1}{a_2+\frac{1}{a_3+\frac{1}{\ddots }}}}$

(Die Kettenbruchdarstellung einer rationalen Zahl $\frac{p}{q}$ ist nicht eindeutig, aber alle Kettenbruchzerlegungen ergeben denselben Knoten $K(p,q)$.)

Das Spiegelbild eines 2-Brücken-Knotens $K(p,q)$ ist $K(p,-q)$. Einen orientierungsumdrehenden Homöomorphismus $(S^3,K(p_1,q_1))\to (S^3,K(p_2,q_2))$ zwischen zwei unterschiedlichen 2-Brücken-Knoten gibt es genau dann, wenn

$p_1=p_2$ und entweder $q_1\equiv -q_{2}modp$ oder $q_1{q}_2\equiv -1modp$ ist.

Insbesondere ist ein 2-Brücken-Knoten genau dann amphichiral, wenn $q^2\equiv -1modp$ ist.

Für 2-Brücken-Verschlingungen (mit 2 Komponenten) gibt es einen orientierungserhaltenden Homöomorphismus genau dann, wenn

$p_1=p_2$ und entweder $q_1\equiv q_{2}mod2p$ oder $q_1{q}_2\equiv 1mod2p$ ist.

Beispiele

Die einzigen Torusknoten unter den 2-Brücken-Knoten sind die $(\pm 2,n)$-Torusknoten.

Alle 2-Brücken-Knoten, die keine Torusknoten sind, sind hyperbolische Knoten.

Die Kleeblattschlinge ist der 2-Brücken-Knoten $K(3,1)$ mit Conway-Normalform $\left[3\right]$, der Achterknoten ist der 2-Brücken-Knoten $K(5,2)$ mit Conway-Normalform $[2,2]$.

KnotInfo gibt eine Liste aller 2-Brücken-Knoten mit bis zu 12 Kreuzungen und berechnet die bekannten Knoteninvarianten.

$K(p,q)$ ist genau dann ein Knoten, wenn $p$ ungerade ist. Wenn $p$ gerade ist, dann besteht die 2-Brücken-Verschlingung aus zwei Komponenten.

Eigenschaften und Invarianten

Die Knotengruppe der 2-Brücken-Verschlingung $K(p,q)$ hat die Präsentierung

$⟨a,b\mid a{b}^{{ϵ}_1}{a}^{{ϵ}_2}\dots b^{{ϵ}_{{\alpha }_1}}{a}^{-1}{b}^{-{ϵ}_{{\alpha }_1}}\dots a^{-{ϵ}_2}{b}^{-{ϵ}_1}⟩$

mit ${ϵ}_k:={(-1)}^{\left[\frac{kp}{q}\right]}$.

Die inkompressiblen Flächen in den Komplementen von 2-Brückenknoten wurden von Hatcher und Thurston klassifiziert. Insbesondere bewiesen sie, dass es keine geschlossenen inkompressiblen Flächen gibt. Wenn $K(p,q)$ kein Torusknoten ist, dann gibt jede Dehn-Chirurgie eine irreduzible 3-Mannigfaltigkeit und fast alle Dehn-Chirurgien geben Mannigfaltigkeiten, die keine Haken-Mannigfaltigkeit und auch keine Seifert-Faserung sind.

Bereits Schubert bewies, dass die 2-fachen verzweigten Überlagerungen Linsenräume sind. Die Klassifikation aller endlichen verzweigten Überlagerungen wurde von Minkus erarbeitet.

Die Komplemente hyperbolischer 2-Brückenknoten (mit Ausnahme des Achterknotens) sind zu keinen anderen Knotenkomplementen außer sich selbst kommensurabel.

Es gibt Formeln für die Berechnung des HOMFLY-Polynoms und insbesondere des Jones-Polynoms von 2-Brücken-Knoten.

Siehe auch

• Montesinos-Knoten

Literatur

• Horst Schubert: Knoten mit zwei Brücken, Mathematische Zeitschrift 65, 133–170 (1956). Vorlage:Doi
• John Conway: An enumeration of knots and links, and some of their algebraic properties. Computational Problems in Abstract Algebra (Proc. Conf., Oxford, 1967) 329–358, Pergamon, Oxford (1970). PDF
• Laurent Siebenmann: Exercices sur les noeuds rationnels, Université Paris-Sud (1975).
• Louis H. Kauffman, Sofia Lambropoulou: On the classification of rational knots, L' Enseignement Mathématique, 49, 357–410 (2003). ArXiv
• C. C. Adams, Das Knotenbuch. Einführung in die mathematische Theorie der Knoten, Spektrum Akademischer Verlag (1995), ISBN 3-86025-338-7

Weblinks

• Tabelle rationaler Knoten mit bis zu 16 Kreuzungen