Statische Lichtstreuung (Polymeranalytik)

Die Statische Lichtstreuung beschreibt die Analyse des zeitlichen Mittelwertes der Intensität des Lichtes, das von Lösungen von Makromolekülen oder von Dispersionen von Teilchen mit Durchmessern deutlich unter 0,1 µm gestreut wird. Lichtstreuung an Teilchen mit Durchmessern im Bereich > 0,1 µm werden über die Formalismen nach Lorenz-Mie bzw. Fraunhofer ausgewertet. Die Analyse der zeitlichen Fluktuation der Intensität des gestreuten Lichtes bezeichnet man als dynamische Lichtstreuung.

Die hier verwendeten mathematischen Beziehungen lassen sich mit geringfügigen Anpassungen auch auf die Streuung anderer elektromagnetischer Wellen und auf die Neutronenstreuung anwenden, solange der unten definierte Betrag des Streuvektors, $q$, deutlich kleiner als das streuende Objekt ist.

Durchführung

Skizze des Strahlenganges bei der Lichtstreuung

Eine Lösung von Makromolekülen mit bekannter Konzentration wird in eine zylindrische Küvette eingefüllt und mit einem monochromatischen Lichtstrahl beleuchtet. Man erfasst die Intensität des gestreuten Lichtes als Funktion des Streuwinkels, $\theta$ (=Winkel zwischen der Ausbreitungsrichtung des Beleuchtungsstahls und der Betrachtungsrichtung). Hierbei steht die Achse der zylindrischen Küvette senkrecht zu der Ebene, die von den beiden oben genannten Richtungen aufgespannt wird. Der Detektor hat eine entsprechende Trägheit, bzw. das detektierte Signal wird über eine entsprechende Zeit gemittelt, so dass die zeitlichen Fluktuationen der Streuintensität keine Rolle spielen. Als Detektor kann ein mechanisch verfahrbarer Einzeldetektor, ein Array mehrerer Detektoren oder ein Flächendetektor verwendet werden. Die Empfindlichkeit der Detektoren und gerätespezifische Parameter werden in der Regel durch Referenzmessungen an einem bekannten Streumedium wie z. B. Toluol ermittelt. Die Messung wird an mehreren Lösungen mit systematisch variierter Konzentration der Makromoleküle wiederholt.

Theorie

Verwendete Symbole:
$I/I_0$ Verhältnis der Intensität des gestreuten Lichtes zur Intensität des eingestrahlten Lichtes
${\lambda }_{\text{vac}}$ Wellenlänge der verwendeten Strahlung im Vakuum
$\lambda ={\lambda }_{\text{vac}}/n$ Wellenlänge der verwendeten Strahlung im Medium mit Brechungsindex $n$
$r_D$ Abstand zwischen Streuzentrum und Detektor
$\alpha$ Polarisierbarkeit eines Teilchens (Atom oder Molekül)
$\theta$ Streuwinkel
$\vartheta$ Polarwinkel in Bezug auf die Dipolachse eines Herzschen Dipols
$V$ beleuchtetes Volumen
$R(\theta ,\rho ),R(\theta ,c)$ Raleigh-Verhältnis
$\rho =N/V$ Teilchendichte (Anzahldichte, Teilchenkonzentration) im beleuchteten Volumen
${\epsilon }_0$ Permittivität des Vacuums
${\epsilon }_r$ Permittivitätszahl
$Z$ Zahl der Teilvolumina
$V_s=V/Z$ Volumen eines Teilvolumens
$Z/V=1/V_s$ Dichte der Teilvolumina im beleuchteten Volumen
$N_s$ Zahl der Teilchen in einem Teilvolumen
${\rho }_s=N_s/V_s$ Teilchendichte in einem Teilvolumen
$\mathrm{\Delta }{\alpha }_s={\mu }_s/E_0$ Verhältnis von induziertem Dipol eines Teilvolumes zum Elektrischen Feld
$⟨{\left(\mathrm{\Delta }{\alpha }_s\right)}^2⟩$ Varianz von $\mathrm{\Delta }{\alpha }_s$
$w=V_s/V$ Wahrscheinlichkeit, dass ein bestimmtes Molekül einem bestimmten Teilvolumen ist
$W(N_s,w)$ Wahrscheinlichkeit, dass ein Teilvolumen die Zahl $N_s$ an Teilchen enthält
$⟨{\left(\mathrm{\Delta }{N}_s\right)}^2⟩$ Varianz der Zahl der Teilchen in den Teilvolumina
$⟨{\left(\mathrm{\Delta }{\rho }_s\right)}^2⟩$ Varianz der Teilchendichte in den Teilvolumina
$S$ Entropie
$k_{\mathrm{B}}$ Boltzmann-Konstante
$\tilde{\mathrm{R}}=N_A{k}_{\mathrm{B}}$ ideale Gaskonstante
$T$ absolute Temperatur
$H$ Enthalpie
$G$ Freie Enthalpie, Gibbs-Energie
$\omega$ Zahl der Möglichkeiten einen thermodynamischen Zustand zu realisieren
${\omega }_0$ Zahl der Möglichkeiten den Zustand des thermodynamischen Minimums zu realisieren
$G_s$ Freie Enthalpie des Teilvolumens
$G_{0,s}$ Freie Enthalpie des Teilvolumens im thermodynamischen Minimum
$p$ Druck
$c$ Massenkonzentration
$N_A$ Avogadrokonstante
$n$ Brechungsindex
$M$ Molmasse
$\mathrm{\Pi }$ Osmotischer Druck
$c_i,m_i,N_i,M_i$ Massenkonzentration, Masse, Teilchenzahl, Molmasse einer (einheitlichen) Teilfraktion innerhalb einer Mischung uneinheitlicher Molmasse
$M_w$ Massenmittel der Molmasse
$1/M$, $A_2$, $A_3$, … erster, zweiter, dritter, … Virialkoeffizient des osmotischen Drucks
$q=\left(4\pi n\right)/\left({\lambda }_{\text{vac}}\right)\cdot \sin (\theta /2)$ Betrag des Streuvektors
$r_j$ Abstand eines lokalen Streuzentrums (Wiederholungseinheit) zum Schwerpunkt eines Makromoleküls
$c_j$ lokale Massenkonzentration der Wiederholungseinheiten eines Makromoleküls in einem lokalen Streuzentrum
${\sigma }_j$ Amplitude einer Welle, die von einem lokalen Streuzenrum (Wiederholungseinheit) in einem Makromolekül ausgeht
$R_g^2$ Streumassenradius
$\vartheta ,\phi$ Polarwinkel und Azimuthwinkel eines Kugelkoordinatensystems

Vereinfacht gesprochen beruht die statische Lichtstreuung an Lösungen von Makromolekülen darauf, dass eine jede Wiederholungseinheit eines gelösten Makromoleküls lokal die Permittivität der Lösung verändert und dort zu einem elektrisch polarisierbaren Bereich führt. Das oszillierende elektrische Feld der eingestrahlten Lichtwelle regt diesen Bereich zu erzwungenen Schwingungen an. Der Bereich verhält sich wie ein oszillierender Hertzscher Dipol und wird somit zu einer Strahlungsquelle.
Bei einem kompakten Makromolekül haben die Wellen, die von den einzelnen Wiederholungseinheiten dieses einen Makromoleküls ausgehen, zueinander keinen Gangunterschied. Bei der Interferenz von Wellen ohne Gangunterschied addieren sich deren Amplituden, d. h. die Amplitude der Welle, die von einem der Makromoleküle ausgeht, ist proportional zur Zahl der Wiederholungseinheiten in diesem Molekül. Die Intensität $I$ einer Welle ist proportional zum Quadrat der Amplitude, hier also proportional zum Quadrat der Zahl der Wiederholungseinheiten in dem einen Makromolekül also proportional zum Quadrat der Molmasse, $M^2$.
Weiterhin erreicht den Detektor Streulicht aus vielen Makromolekülen die entlang des Strahlenganges auf Längen deutlich über der Wellenlänge zufällig verteilt sind. Bei der Interferenz von Wellen, die von zufällig verteilten Objekten ausgehen, addieren sich nicht wie im vorherigen Fall die Amplituden, sondern die Intensitäten der Wellen. Somit ist die Intensität am Detektor proportional zur Intensität der Strahlung aus dem einzelnen Makromolekül multipliziert mit der Zahl der Makromoleküle im Strahlengang. Letztere ist proportional zum Verhältnis von Massenkonzentration zu Molmasse, $c/M$.
Somit ist die Intensität am Detektor proportional zum Produkt aus Molmasse und Massenkonzentration, $I\propto M^2\cdot c/M\propto M\cdot c$.
Aus dem Verhältnis der Intensität zur Konzentration erhalten wir die Molmasse, $M\propto I/c$.

Etwas genauer betrachtet wird die Lichtstreuung zusätzlich – je nach System sogar erheblich – davon beeinflusst, dass i) die gelösten Moleküle miteinander und mit dem Lösungsmittel wechselwirken und ii) die Makromoleküle so groß sind, dass das Streulicht durch Interferenz innerhalb des Moleküls abgeschwächt wird. Dies könnte man einerseits als 'lästig' empfinden, andererseits kann Lichtstreuung so auch Aussagen über die Molmassenverteilung, die Wechselwirkung mit dem Lösungsmittel (Virialkoeffizienten des Osmotischen Druckes, $A_2$, $A_3$, …) und die räumliche Ausdehnung der gelösten Makromoleküle (Streumassenradius, $R_g^2$) geben.

Lichtstreuung von Gasen und überkritischen Fluiden

Ideale Gase

Zwei unterschiedliche Betrachtungsweisen führen letztendlich zu dem gleichen Ergebnis:

Streuung an Einzelmolekülen

Rayleigh-Streuung beschreibt die Lichtstreuung durch $N$ Einzelmoleküle eines Gases (leerer Raum zwischen den Gasmolekülen, hohe Verdünnung) als Funktion ihrer Polarisierbarkeit $\alpha$.

$\frac{I}{I_0}=\frac{{\pi }^2{\alpha }^2}{{{\epsilon }_0}^2{\lambda }^4}\frac{1}{{r_D}^2}\frac{1+{\cos }^2(\theta )}{2}N(1)$

Auswirkung der Polarisation auf die Abstrahlung eines Hertz’schen Dipols

Hierbei beschreibt $I/I_0$ das Verhältnis der Intensität des detektierten Lichtes zur Intensität des eingestrahlten Lichtes, der erste Bruch rechts des Gleichheitszeichens die Wechselwirkung des Moleküls mit der eingehenden Strahlung der Wellenlänge $\lambda$ in SI-Einheiten, der zweite die Abhängigkeit der Lichtintensität vom Abstand zwischen Quelle und Detektor $r_D$, und der dritte berücksichtigt, dass das eingehende Licht unpolarisiert ist, die Intensität der Streuung somit für den s-polarisierten Anteil winkelunabhängig, für den p-polarisierten Anteil hingegen $\sim {\cos }^2(\theta )$ ist (Siehe Hertzscher Dipol; der hier mit $\theta$ bezeichnete Winkel ist der Streuwinkel, bei der Beschreibung eines Hertzschen Dipols wird mit $\vartheta$ meist der Polarwinkel in Bezug auf die Dipolachse bezeichnet. Bei s-Polarisation gilt $\vartheta =90^{\circ }$ unabhängig von $\theta$. Bei p-Polarisation gilt $\vartheta =90^{\circ }-\theta$ und $1-{\cos }^2(\vartheta )={\cos }^2(\theta )$.)

Zur Vereinfachung teilen wir beide Seiten durch die Winkelabhängigkeit und durch gerätespezifische Parameter wie den Abstand des Detektors von der Küvette, $r_D$, und das beleuchtete Volumen, $V$, und erhalten so das sogenannte Raleigh-Verhältnis, $R(\theta ,\rho )$

$R(\theta ,\rho )=\frac{I}{I_0}\frac{{r_D}^2}{(1+{\cos }^2\theta )V}=\frac{{\pi }^2{\alpha }^2}{2{{\epsilon }_0}^2{\lambda }^4}\rho (2)$

Dieses ist proportional zur Teilchendichte (Anzahldichte) des Gases, $\rho$.

Streuung an Konzentrationsfluktuationen:

Zufällig platzierte schwarze Punkte; daraus erzeugte Graustufenbilder in unterschiedlicher Auflösung

Auf hinreichend kleinen Längenskalen betrachtet, hat ein ideales Gas nicht an jedem Ort die gleiche Teilchendichte und somit auch nicht die gleiche Permittivität. Um dies zu illustrieren, wurden für die nebenstehende Abbildung viele schwarze Punkte zufällig auf eine weiße Fläche verteilt. Man sieht ein typisches 'Sandbild'. Wandeln wir dies in Graustufenbilder um und variieren die Auflösung, so erkennt man, dass auch auf Lägenskalen deutlich größer als der Durchmesser der Punkte noch Variationen im Grauwert der Pixel auftreten. Diese Variationen steigen mit abnehmender Pixelgröße.

Um dies mathematisch zu beschreiben, teilen wir das gesamte beleuchtete Volumen in eine große Zahl, $Z$, von kleinen Teilvolumina ,$V_s\ll V$ und ersetzen in Gleichung(2) die Anzahldichte der Teilchen $\rho$ durch die Anzahldichte der Teilvolumina $\rho \to Z/V=1/V_s$. Wir gehen davon aus, dass die Permittivitätszahl eines Teilvolumens ${\epsilon }_{r,s}$ sich von der mittleren Permittivitätszahl seiner Umgebung ${\epsilon }_r$ um einen kleinen Betrag, $\mathrm{\Delta }{\epsilon }_{\mathrm{r},\mathrm{s}}={\epsilon }_{r,s}-{\epsilon }_r\ll {\epsilon }_r$, unterscheidet. Das elektrische Feld der eingestrahlten Lichtwelle, $E_0$ induziert in diesem Volumen ein Dipolmoment $\mu$. Das Verhältnis $\mu /E_0$ nennen wir $\mathrm{\Delta }{\alpha }_s$. Allerdings ist die Abweichung der Teilvolumina vom Mittelwert statistisch verteilt. D. h. wir können ${\alpha }^2$ in Gleichung (2) nicht durch einen einzelnen Wert ${\left(\mathrm{\Delta }{\alpha }_s\right)}^2$ ersetzten, sondern müssen den Mittelwert $⟨{\left(\mathrm{\Delta }{\alpha }_s\right)}^2⟩$ verwenden (dies ist die Varianz von $\mathrm{\Delta }{\alpha }_s$). Wir erhalten somit:

$R(\theta ,\rho )=\frac{{\pi }^2⟨{\left(\mathrm{\Delta }{\alpha }_s\right)}^2⟩}{2{{\epsilon }_0}^2{\lambda }^4}\frac{1}{V_s}(3)$

$\mathrm{\Delta }{\alpha }_s$ lässt sich über die Clausius-Mossotti-Gleichung (SI-System) für eine dielektrische Kugel in einer dielektrischen Umgebung aus den Permittivitätszahlen berechnen nach:

$\frac{{\mu }_s}{E_0}=\mathrm{\Delta }{\alpha }_s$$=V_s\cdot {\epsilon }_0\cdot 3{\epsilon }_r\frac{{\epsilon }_{r,s}-{\epsilon }_r}{{\epsilon }_{r,s}+2{\epsilon }_r}$$=V_s\cdot {\epsilon }_0\cdot 3{\epsilon }_r\frac{\mathrm{\Delta }{\epsilon }_{\mathrm{r},s}}{\mathrm{\Delta }{\epsilon }_{\mathrm{r},s}+3{\epsilon }_{\mathrm{r}}}$$\approx V_s\cdot {\epsilon }_0\cdot \mathrm{\Delta }{\epsilon }_{\mathrm{r},s}\to$$\frac{d\mathrm{\Delta }{\alpha }_s}{d{\epsilon }_{r,s}}\approx V_s\cdot {\epsilon }_0(4)$

Weiterhin ist die Störung klein genug, dass wir eine lineare Abhängigkeit der Permittivität von der Teilchendichte annehmen können.

Somit ergibt sich der folgende Zusammenhang zwischen der Varianz der Polarisierbarkeit und der Varianz der Teilchendichte:

$⟨{\left(\mathrm{\Delta }{\alpha }_s\right)}^2⟩$$=(d\mathrm{\Delta }{\alpha }_s/d{{\epsilon }_r}_s{)}^2\cdot {(d{\epsilon }_r/d\rho )}^2\cdot ⟨{\left(\mathrm{\Delta }{\rho }_s\right)}^2⟩$$=V_s^2{\epsilon }_0^2{(d{\epsilon }_r/d\rho )}^2\cdot ⟨{\left(\mathrm{\Delta }{\rho }_s\right)}^2⟩(5)$

(da wir hier nur die Ableitungen benötigen, können wir statt $d\mathrm{\Delta }{\epsilon }_r$ und $d\mathrm{\Delta }\rho$ auch einfach $d{\epsilon }_r$ und $d\rho$ schreiben.)

Die Wahrscheinlichkeit, dass ein Molekül des idealen Gases in eines der Teilvolumina gelangt, beträgt $w=1/Z=V_s/V$. Die Wahrscheinlichkeit, $W(N_s,w)$, dass eines dieser Teilvolumina die Zahl $N_s$ an Teilchen enthält, lässt sich durch die Binomialverteilung beschreiben. Für große $N$ und den Grenzfall $w\ll 1\iff V_s\ll V$ hat diese Binomialverteilung eine Varianz der Zahl der Teilchen in den Teilvolumina von

$⟨{\left(\mathrm{\Delta }{N}_s\right)}^2⟩=N\cdot w=N\cdot V_s/V=\rho \cdot V_s(6)$

Wir teilen beide Seiten durch $V_s^2$ und erhalten:

$⟨{\left(\mathrm{\Delta }{\rho }_s\right)}^2⟩=\rho /V_s(7)$

D.h. ähnlich wie die Varianz der Grauwerte auf dem nebenstehenden Bild mit abnehmender Pixelgröße steigt, steigt die Varianz der Anzahldichte der Teilchen in den Teilvolumina zum Streulicht mit abnehmendem Teilvolumen; gleichzeitig sinkt natürlich der Beitrag eines einzelnen Teilvolumens mit abnehmendem Volumen. Dies führt letztendlich dazu, dass das Ergebnis unserer Herleitung (z. B. die unten folgende Gleichung (8)) nicht von der willkürlich gewählten Größe des Teilvolumens, $V_s$, abhängt.

Setzen wir Gleichung (5) und Gleichung(7) in Gleichung (3) ein, erhalten wir:

$R(\theta ,\rho )=\frac{{\pi }^2{V}_s^2{{\epsilon }_0}^2(d{\epsilon }_r/d\rho {)}^2\rho /V_s}{2{{\epsilon }_0}^2{\lambda }^4}\frac{1}{V_s}=\frac{{\pi }^2(d{\epsilon }_r/d\rho {)}^2}{2{\lambda }^4}\rho (8)$

Für die weiter unten folgenden Beschreibungen genügt es anzunehmen, dass die Permittivitätszahl eine lineare Funktion der Teilchendichte ist. Für die Beschreibung von Gasen ist es instruktiv, den Zusammenhang zwischen Teilchendichte und Permittivitätszahl zu betrachten (Clausius-Mossotti-Gleichung, SI-System):

$\rho \cdot \alpha ={\epsilon }_0\cdot 3\frac{{\epsilon }_{\mathrm{r}}-1}{{\epsilon }_{\mathrm{r}}+2}\iff$ ${\epsilon }_{\mathrm{r}}=1+\frac{\rho \cdot \alpha }{{\epsilon }_0-\frac{1}{3}\cdot \rho \cdot \alpha }\to$$\frac{d{\epsilon }_r}{d\rho }=\frac{\alpha {\epsilon }_0}{{({\epsilon }_0-\frac{1}{3}\rho \alpha )}^2}(9)$

Bei Gasen ist i. d. R. die Teilchendichte so niedrig, dass $\alpha \rho \ll {\epsilon }_0$ ist; man erhält in guter Näherung

$\frac{d{\epsilon }_r}{d\rho }\approx \frac{\alpha }{{\epsilon }_0}(10)$

Setzen wir Gleichung (10) in Gleichung (8) ein, erhalten wir wieder Gleichung(2).

Zur Beschreibung der Lichtstreuung durch ein ideales Gas erhalten wir das gleiche Ergebnis unabhängig davon, ob wir Streuung durch einzelne Teilchen im leeren Raum oder Streuung durch Konzentrationsfluktuationen zugrunde legen. Der zweite Weg jedoch lässt sich auf einfache Weise auf nichtideale Fluide erweitern.

Reale Gase und überkritische Fluide

Auch reale Gase, Flüssigkeiten, überkritische Fluide und Gläser streuen Licht, diese Streuung wird ebenfalls durch Dichtefluktuationen hervorgerufen, allerdings ist die o. g. Beschreibung der Fluktuationen über eine einfache Binomialverteilung nicht mehr ausreichend. Sie lässt sich jedoch aus thermodynamischen Überlegungen ableiten:

In den meisten thermodynamischen Überlegungen können wir gefahrlos davon ausgehen, dass alle Teilvolumina die durchschnittliche Zahl an Molekülen enthalten; hier jedoch ist wichtig, dass ein Teilvolumen auch eine vom Durchschnitt abweichende Zahl an Molekülen enthalten kann, dass dessen Wahrscheinlichkeit umso geringer ist, je weiter die Zahl vom Durchschnitt abweicht jedoch nicht gleich $0$ ist. Die Boltzmann-Beziehung setzt die Häufigkeit, $\omega$, eines Zustandes eines isoliert von der Umgebung betrachteten Systems oder Teiles eines Systems in Beziehung zu seiner Entropie, $S$:

$\omega =\exp \left(\frac{S}{k_{\mathrm{B}}}\right)(11)$

Wenn ein System mit der Umgebung Wärme austauscht, bewirkt dies auch außerhalb des Systems eine Entropieveränderung. Bei einem isobaren, isothermen System ist die Summe aller Entropieänderungen (im System + in der Umgebung) gleich dem negativen Quotienten aus Änderung der freien Enthalpie, $\mathrm{\Delta }G$, und der absoluten Temperatur, $T$:

$\underset{\text{im System}}{\underbrace{\mathrm{\Delta }S}}-\underset{\text{Austausch mit der Umgebung}}{\underbrace{\frac{\mathrm{\Delta }H}{T}}}=-\frac{\mathrm{\Delta }G}{T}(12)$.

Weicht also eines der Teilvolumina von der Gleichverteilung ab, so ergibt sich unter isothermen und isobaren Randbedingungen die Änderung der Häufigkeit dieses abweichenden Zustandes aus der Änderung der freien Enthalpie dieses Zustandes gegenüber der Gleichverteilung, $G_s-G_{0,s}$. Wir erhalten somit:

$\frac{{\omega }_s}{{\omega }_{0,s}}=\exp (-\frac{G_s-G_{0,s}}{k_{B}T})(13)$

$G_s-G_{0,s}$ ist eine Funktion von $\mathrm{\Delta }{\rho }_s$ und hat bei $\mathrm{\Delta }{\rho }_s=0$ den Wert $0$ und ein Minimum, d. h. auch die erste Ableitung nach der Teilchendichte $\mathrm{d}{G}_s/\mathrm{d}{\rho }_s$ beträgt $0$. Wir beschreiben die Abhängigkeit $G_s-G_{0,s}=f(\mathrm{\Delta }{\rho }_s))$, durch eine Taylorreihenentwicklung 2. Grades.

$G_s-G_{0,s}=(G_{0,s}-G_{0,s})+\frac{\mathrm{d}{G}_s}{\mathrm{d}{\rho }_s}\mathrm{\Delta }{\rho }_s+\frac{1}{2}\frac{{\mathrm{d}}^2{G}_s}{\mathrm{d}{{\rho }_s}^2}{\left(\mathrm{\Delta }{\rho }_s\right)}^2(14)$

Die ersten beiden Glieder dieser Taylorreihenentwicklung betragen $0$, so dass wir einen einfachen Ausdruck erhalten.

$\frac{{\omega }_s}{{\omega }_{0,s}}=\exp (-\frac{1}{2}\frac{1}{k_{B}T}\frac{{\mathrm{d}}^2{G}_s}{\mathrm{d}{{\rho }_s}^2}{\left(\mathrm{\Delta }{\rho }_s\right)}^2)(15)$

Dies bedeutet, $\mathrm{\Delta }{\rho }_s$ ist normalverteilt mit einer Varianz von:

$⟨{\left(\mathrm{\Delta }{\rho }_s\right)}^2⟩=k_{\mathrm{B}}T\cdot \frac{1}{\frac{{\mathrm{d}}^2{G}_s}{\mathrm{d}{{\rho }_s}^2}}(16)$

Der Gibbs-Duhem-Gleichung zufolge besteht für ein isothermes Einkomponentensystem, das einer kleinen Störung unterworfen wird, die folgende Beziehung zwischen der Änderung des chemischen Potentials und der Änderung des Drucks, p:

$N_s\cdot \mathrm{d}\left(\frac{\mathrm{d}{G}_s}{\mathrm{d}{N}_s}\right)=V_s\mathrm{d}p(17)$

In unserem Falle sei die kleine Störung eine Änderung der Teilchenzahl, $d{N}_s$, somit erhalten wir:

$N_s\cdot \frac{\mathrm{d}}{\mathrm{d}{N}_s}\left(\frac{\mathrm{d}{G}_s}{\mathrm{d}{N}_s}\right)=V_s\frac{\mathrm{d}{p}_s}{\mathrm{d}{N}_s}$$\iff \frac{{\mathrm{d}}^2{G}_s}{\mathrm{d}{N}_s^2}$$=\frac{1}{{\rho }_s}\frac{\mathrm{d}{p}_s}{\mathrm{d}{N}_s}\iff$$\frac{{\mathrm{d}}^2{G}_s}{\mathrm{d}{\rho }_s^2}=\frac{1}{{\rho }_s}\frac{\mathrm{d}{p}_s}{\mathrm{d}{\rho }_s}\cdot V_s\approx \frac{1}{\rho }\frac{\mathrm{d}p}{\mathrm{d}\rho }\cdot V_s(18)$

hierbei haben wir im letzten Schritt beide Seiten mit $V_s^2$ multipliziert und angewendet, dass die Dichte und Kompressibilität des Teilvolumens nahezu identisch zu den entsprechenden Werten des gesamten beleuchteten Volumens sind.

Daraus erhalten wir:

$⟨{\left(\mathrm{\Delta }{\rho }_s\right)}^2⟩=k_{\mathrm{B}}T\frac{\rho }{\mathrm{d}p/\mathrm{d}\rho }\cdot \frac{1}{V_s}(19)$

Diese können wir in Gleichung (5) einsetzen und erhalten:

$R(\theta ,\rho )=\frac{{\pi }^2{V}_s^2(\mathrm{d}{\epsilon }_r/\mathrm{d}{\rho }_s{)}^2{k}_{\mathrm{B}}T\frac{\rho }{\mathrm{d}p/\mathrm{d}\rho }\cdot \frac{1}{V_s}}{2{\lambda }^4}\frac{1}{V_s}=\frac{{\pi }^2(\mathrm{d}{\epsilon }_r/\mathrm{d}{\rho }_s{)}^2}{2{\lambda }^4\frac{1}{k_{\mathrm{B}}T}\frac{\mathrm{d}p}{\mathrm{d}\rho }}\cdot \rho (20)$

Bei idealen Gasen gilt $\mathrm{d}p/\mathrm{d}\rho =k_{\mathrm{B}}T$ und man erhält auch aus diesen Überlegungen erneut Gleichung(7) Gleichung(8) und Gleichung(2).

Bei realen Gasen ergibt sich aufgrund der Wechselwirkung zwischen den Teilchen eine stärkere Dichtefluktuation und somit eine stärkere Streuung. Dieser Effekt ist besonders stark in der Nähe des kritischen Punktes, dort ist $\mathrm{d}p/\mathrm{d}\rho$ nahe null und man erhält starke Lichtstreuung, obwohl das überkritische Fluid noch nicht phasensepariert ist.

Lichtstreuung an Gasen und überkritischen Fluiden wird i. d. R. nicht zur Bestimmung von Molekülmassen verwendet. Über Gleichung (2) kann man aus der Lichtstreuung verdünnter Gase weit oberhalb der kritischen Temperatur unter Kenntnis der Molekülmasse und Massendichte des Gases die Polarisierbarkeit, $\alpha$, von Gasmolekülen berechnen. Bei überkritischen Fluiden in der Nähe des kritischen Punktes hingegen zieht man aus der Lichtstreuung hauptsächlich Erkenntnisse über die zwischenmolekularen Wechselwirkungen und die Struktur und Kinetik der Konzentrationsfluktuationen.

Lichtstreuung an Lösungen hingegen wird häufig durchgeführt um die Molmasse der gelösten Substanz zu ermitteln.

Lichtstreuung von Lösungen

Ideale Lösungen

Gelöste Einzelmoleküle, die sich in ihrer Polarisierbarkeit von dem Lösungsmittel unterscheiden, erhöhen im Vergleich zum reinen Lösungsmittel die Lichtstreuung. Dieser Effekt ist in der Regel deutlich stärker als die Streuung durch die Dichtefluktuationen in der Lösung. Wir ermitteln somit zunächst die Lichtstreuung durch das reine Lösungsmittel, dann die durch die Lösung und betrachten deren Differenz, $\mathrm{\Delta }R(\theta ,c)=R(\theta ,c)-R(\theta ,\mathrm{L}\ddot{\mathrm{o}}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{l})$. Bei einer idealen Lösung können wir Gleichung (8) wie folgt von Gasen auf Lösungen übertragen:

Experimentell ist es einfach den Brechungsindex $n$ als Funktion der Massenkonzentration $c=M\rho /N_A$ zu ermitteln. Für niedrige Konzentrationen ist diese Beziehung linear, so dass wir aus wenigen Messungen leicht die Ableitung $\mathrm{d}n/\mathrm{d}c$ bestimmen können. Weiterhin gilt $n^2={\epsilon }_r$ und $\mathrm{d}{\epsilon }_r/\mathrm{d}n=2n$. Wir erhalten somit:

$\mathrm{d}{\epsilon }_r/\mathrm{d}\rho =(\mathrm{d}{\epsilon }_r/\mathrm{d}n)(\mathrm{d}n/\mathrm{d}c)(\mathrm{d}c/\mathrm{d}\rho )=2n(\mathrm{d}n/\mathrm{d}c)M/N_A(21)$

Die Lösung ist i. d. R. verdünnt genug, dass wir hier für $n$ den Brechungsindex des reinen Lösungsmittels verwenden können.

Ersetzen wir in Gleichung (9) $\rho \to c{N}_A/M$ und $\mathrm{d}{\epsilon }_r/\mathrm{d}\rho \to 2n(\mathrm{d}n/\mathrm{d}c)M/N_A$ erhalten wir:

$\mathrm{\Delta }R(\theta ,c)=\frac{{\pi }^2(2n(\mathrm{d}n/\mathrm{d}c)M/N_A{)}^2}{2{\lambda }^4}\cdot c{N}_A/M=\frac{2{\pi }^2{n}^2(\mathrm{d}n/\mathrm{d}c{)}^{2}M}{{\lambda }^4{N}_A}\cdot c=K\cdot c\cdot M(22)$

mit $K=\frac{2{\pi }^2{n}^2{(\mathrm{d}n/\mathrm{d}c)}^2}{{\lambda }^4{N}_A}(23)$

Die physikalischen Größen, aus denen K berechnet wird, sind leicht zugänglich, so dass man die Molmasse berechnen könnte nach:

$M=\frac{\mathrm{\Delta }R(\theta ,c)}{K\cdot c}(24)$

Nicht einheitliche Molmassen

Haben die Makromoleküle keine einheitliche Molmasse, so ist die Streuintensität gleich der Summe der Teilintensitäten aller Fraktionen, $\mathrm{\Delta }R(\theta ,c)={\mathrm{\Sigma }}_i\mathrm{\Delta }R(\theta ,c{)}_i$, und die Gesamtkonzentration gleich der Summe der Teilkonzentrationen dieser Fraktionen , $c={\mathrm{\Sigma }}_i{c}_i$ , somit erhalten wir:

$\frac{\mathrm{\Delta }R(\theta ,c)}{K\cdot c}=\frac{\sum _i\mathrm{\Delta }R(\theta ,c{)}_i}{K\cdot \sum _i{c}_i}=\frac{\sum _i{c}_i{M}_i}{\sum _i{c}_i}=\frac{\sum _i{m}_i{M}_i}{\sum _i{m}_i}=\frac{\sum _i{N}_i{M}_i^2}{\sum _i{N}_i{M}_i}=M_w(25)$

D. h. statische Lichtstreuung liefert bei uneinheitlichen Makromolekülen das Massenmittel der Molmasse.

Nicht ideale Lösungen

In den meisten Fällen müssen wir berücksichtigen, dass die Lösungen nicht ideal sind. Wie bei der obigen Beschreibung der Lichtstreuung durch Gase nehmen wir nun an, dass die Lichtstreuung durch Konzentrationsfluktuationen hervorgerufen wird. Bei der Beschreibung von Lösungen hat der osmotische Druck die gleiche Bedeutung, wie bei der Beschreibung von Gasen der Druck. D. h. wir ersetzen in Gleichung (20): $\rho \to c{N}_A/M$, $\mathrm{d}{\epsilon }_r/\mathrm{d}\rho \to 2n(\mathrm{d}n/\mathrm{d}c)M/N_A$ und $p\to \mathrm{\Pi }$ und erhalten:

$\mathrm{\Delta }R(\theta ,c)=\frac{{\pi }^2(2n(\mathrm{d}n/\mathrm{d}c)M/N_A{)}^2}{2{\lambda }^4\frac{1}{k_{\mathrm{B}}T}\frac{\mathrm{d}\mathrm{\Pi }}{\mathrm{d}c{N}_A/M}}\cdot c{N}_A/M=\frac{2{\pi }^2{n}^2((\mathrm{d}n/\mathrm{d}c){)}^2}{{\lambda }^4{N}_A\frac{1}{\tilde{\mathrm{R}}T}\frac{\mathrm{d}\mathrm{\Pi }}{\mathrm{d}c}}\cdot c=\frac{K\cdot c}{\frac{1}{\tilde{\mathrm{R}}T}\frac{\mathrm{d}\mathrm{\Pi }}{\mathrm{d}c}}(26)$

Bei einer idealen Lösung beträgt

$\frac{\mathrm{\Pi }}{\tilde{\mathrm{R}}T}=\frac{1}{M}\cdot c\Rightarrow \frac{1}{\tilde{\mathrm{R}}T}\frac{\mathrm{d}\mathrm{\Pi }}{\mathrm{d}c}=\frac{1}{M}(27)$

und man erhält aus Gleichung (26) wieder Gleichung (22). Bei nicht idealen Lösungen wird die Abweichung von der Idealität oft durch eine Reihenentwicklung beschrieben:

$\frac{\mathrm{\Pi }}{\tilde{\mathrm{R}}T}=\frac{1}{M}\cdot c+A_2\cdot c^2+A_3\cdot c^3+\dots \Rightarrow \frac{1}{\tilde{\mathrm{R}}T}\frac{\mathrm{d}\mathrm{\Pi }}{\mathrm{d}c}=\frac{1}{M}+2A_2\cdot c+3A_3\cdot c^2+\dots (28)$

Die Faktoren $1/M$, $A_2$, $A_3$, … bezeichnet man als die Virialkoeffizienten des osmotischen Drucks. > Somit ergibt sich bei nichtidealen Lösungen:

$\frac{K\cdot c}{\mathrm{\Delta }R(\theta ,c)}=\frac{1}{M}+2A_{2}c+3A_3{c}^2+\dots (29)$

Man führt Lichtstreuung meist an Lösungen der Makromoleküle in einem 'guten Lösungsmittel' durch, in diesem Falle sind die Konzentrationsfluktuationen geringer als im Fall einer idealen Lösung ($A_2$ ist positiv) und die Lichtstreuung wird im Vergleich zu einer idealen Lösung abgeschwächt.

Interferenz innerhalb großer Moleküle

Zwei Grenzfälle der Interferenz von Wellen, die von vielen unterschiedlichen Streuzentren ausgehen, haben wir implizit oben schon angewendet: Befinden sich alle diese Streuzentren an einem Punkt, so sind die von den Streuzentren ausgehenden Wellen in Phase, es addieren sich die Amplituden der einzelnen Wellen, die Intensität des gesamten Streulichtes ist proportional zum Quadrat der Zahl an Streuzentren in diesem Punkt. Sind die Streuzentren über Abstände viel größer als die Wellenlänge zufällig verteilt, so addieren sich die Intensitäten, die Intensität des gesamten Streulichtes ist proportional zur Zahl der Streuzentren.

Bei einem Makromolekül ist die räumliche Ausdehnung oft so groß, dass Streulicht, das von verschiedenen Wiederholungseinheiten eines Moleküls ausgeht, nicht mehr vollständig in Phase ist. Andererseits stehen die Wiederholungseinheiten in definierter räumlicher Beziehung zueinander und sind deutlich geringer als eine Wellenlänge voneinander entfernt. Diese führt im Vergleich zu dem Fall, dass alle Wiederholungseinheiten in einem Punkt konzentriert wären, zu einer leichten Abschwächung des Streulichtes. Bei gleichbleibender Molekülmasse ist diese Abschwächung um so größer, je größer das Volumen ist, auf das sich das Makromolekül ausbreitet.
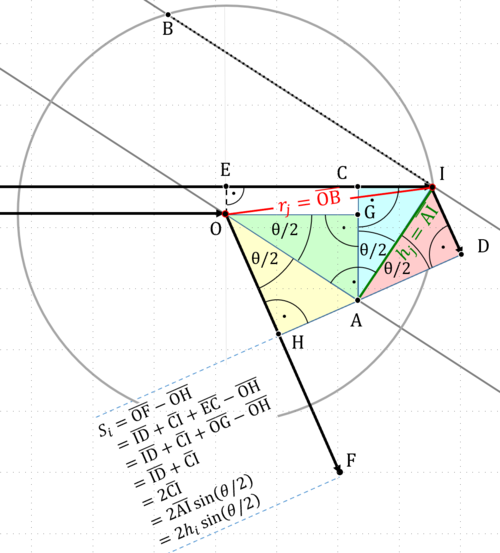
Für eine mathematische Beschreibung dieses Phänomens betrachten wir nebenstehende Abbildung. In dieser ist die Position eines Streuzentrums mit $\mathrm{I}$, die des Schwerpunktes eines Makromoleküls mit $\mathrm{O}$ bezeichnet. Den Abstand des Streuzentrums $\mathrm{I}$ vom Schwerpunkt $\mathrm{O}$ bezeichnen wir mit $r_j$. Hierbei können wir entweder davon ausgehen, dass eine jede Wiederholungseinheit ein Streuzentrum sei und jedes Streuzentrum Strahlung der gleichen Amplitude, ${\sigma }_j$, erzeugt, oder einem Streuzentrum ein bestimmtes Volumen $\mathrm{d}{V}_j$ und eine Massenkonzentration an Wiederholungseinheiten $c_j$ zuordnen und davon ausgehen, dass die Amplitude der gestreuten Strahlung proportional zum Produkt dieser beiden Größen ist ${\sigma }_j\sim c_j\cdot \mathrm{d}{V}_j$. Diese Betrachtung lässt sich einfach auf Copolymere ausweiten, indem wir anstelle der lokalen Massenkonzentration einer Art von Wiederholungseinheiten die Produkte aus den Konzentrationen der unterschiedlichen Wiederholungseinheiten mit den Werten von $\mathrm{d}n/\mathrm{d}c$ der jeweiligen Homopolymere aufsummieren.
Für die weitere Herleitung ist nicht entscheidend, ob aus dem Schwerpunkt tatsächlich Streulicht kommt, letztendlich genügt es, den Schwerpunkt als Referenzpunkt zu verwenden.
Die Welle, die vom Streuzentrum $\mathrm{I}$ ausgeht, benennen wir $E_j(X)$. Sie hat im Bezug zur (hypothetischen) Welle aus dem Schwerpunkt den Gangunterschied $S_j$ und eine Amplitude ${\sigma }_j$. In nebenstehender Abbildung liegen die beiden grauen Geraden auf Ebenen, die senkrecht zur Ebene der Abbildung und parallel zur Winkelhalbierenden des Streuwinkels liegen. Den Abstand dieser beiden Ebenen zueinander bezeichnen wir mit $h_j$, wobei $h_j$ ein positives Vorzeichen hat, wenn das Streuzenrum vom Detektor aus gesehen sich hinter der Ebene durch den Schwerpunkt befindet, und ein negatives, wenn das Streuzentrum davor liegt.
In dem Diagramm sind zwei Strahlengänge eingezeichnet: Licht, dass von Schwerpunkt $\mathrm{O}$ gestreut wird, geht über die Punkte $\mathrm{H}$ und $\mathrm{F}$ und weiter zum Detektor; Licht, dass von Streuzentrum $\mathrm{I}$ gestreut wird geht über die Punkte $\mathrm{E}$,$\mathrm{C}$,$\mathrm{I}$ und $\mathrm{D}$ und weiter zum Detektor. Der Pfad von $\mathrm{E}$ über $\mathrm{C}$ und $\mathrm{I}$ nach $\mathrm{D}$ sei genau so lang, wie der Pfad von $\mathrm{O}$ nach $\mathrm{F}$. Der Gangunterschied zwischen diesen beiden Strahlen, $S_j$, lässt sich aus einfachen geometrischen Überlegungen herleiten:
Die Strecken $\overline{\mathrm{C}\mathrm{G}}$ und $\overline{\mathrm{E}\mathrm{O}}$ stehen senkrecht zur Beleuchtungsrichtung, somit ist $\overline{\mathrm{O}\mathrm{G}}=\overline{\mathrm{E}\mathrm{C}}$. Die Dreiecke $\mathrm{△}\mathrm{A}\mathrm{G}\mathrm{O}$ und $\mathrm{△}\mathrm{A}\mathrm{O}\mathrm{H}$ sind kongruent somit ist $\overline{\mathrm{O}\mathrm{G}}=\overline{\mathrm{O}\mathrm{H}}$. Die Dreiecke $\mathrm{△}\mathrm{A}\mathrm{D}\mathrm{I}$ und $\mathrm{△}\mathrm{A}\mathrm{I}\mathrm{C}$ sind kongruent, somit ist $\overline{\mathrm{C}\mathrm{I}}=\overline{\mathrm{I}\mathrm{D}}$. Ebene Trigonometrie gibt uns den Zusammenhang zwischen $\overline{\mathrm{C}\mathrm{I}}$, dem Abstand der beiden Ebenen und dem halben Streuwinkel: $\overline{\mathrm{C}\mathrm{I}}=h_j\cdot \sin (\theta /2)$. Somit erhalten wir:

$S_j=\overline{\mathrm{H}\mathrm{F}}$
$=\overline{\mathrm{O}\mathrm{F}}-\overline{\mathrm{O}\mathrm{H}}$
$=\overline{\mathrm{I}\mathrm{D}}+\overline{\mathrm{C}\mathrm{I}}+\overline{\mathrm{E}\mathrm{C}}-\overline{\mathrm{O}\mathrm{H}}$
$=\overline{\mathrm{I}\mathrm{D}}+\overline{\mathrm{C}\mathrm{I}}+\overline{\mathrm{O}\mathrm{G}}-\overline{\mathrm{O}\mathrm{H}}$
$=\overline{\mathrm{I}\mathrm{D}}+\overline{\mathrm{C}\mathrm{I}}$
$=2\cdot \overline{\mathrm{C}\mathrm{I}}$
$=2\cdot \overline{\mathrm{A}\mathrm{I}}\cdot \sin (\theta /2)$
$=2\cdot h_j\cdot \sin (\theta /2)(30)$

Eine Welle ist eine Funktion von Ort und Zeit; der Einfachheit halber betrachten wir hier einen 'Schnappschuss' und nehmen nicht die Zeitabhängigkeit, sondern nur die Ortsabhängigkeit der Welle (X=Ortskoordinate in Ausbreitungsrichtung) in die folgenden Formeln auf. Wir beschreiben die Welle, die aus dem Streuzentrum $\mathrm{I}$ kommt mit einer Sinusfunktion des Ortes $X$ ($X$ =Ortskoordinate in Ausbreitungsrichtung) und einem Gangunterschied $S_j$ gegenüber dem Strahl aus dem Schwerpunkt:

$E_j(X)=$
${\sigma }_j\cdot \sin (\frac{2\pi }{\lambda }\cdot (X+S_j))=$
${\sigma }_j\cdot \sin (\frac{2\pi }{\lambda }\cdot (X+2h_j\sin \frac{\theta }{2}))=$
${\sigma }_j\cdot \sin (\frac{2\pi }{\lambda }X+q\cdot h_j)(31)$

mit $q=\frac{4\pi }{\lambda }\cdot \sin \frac{\theta }{2}=\frac{4\pi n}{{\lambda }_{\text{vac}}}\cdot \sin \frac{\theta }{2}(32)$

Über die die Additionsregeln trigonometrischer Funktionen können wir diese Welle ausdrücken als die Summe zweier Wellen; eine Welle ohne Gangunterschied zur Welle aus dem Schwerpunkt und eine Welle mit einem Gangunterschied von $\lambda /4$ (diese wird hier ausgedrückt als Cosinusfunktion des Ortes $X$):

$E_j(X)={\sigma }_j\cdot \cos (q\cdot h_j)\cdot \sin (\frac{2\pi }{\lambda }\cdot X)+{\sigma }_j\cdot \sin (q\cdot h_j)\cdot \cos (\frac{2\pi }{\lambda }\cdot X)(33)$

Die beiden springenden Punkte im Verständnis der nächsten Zeilen sind:
a) die beiden ortsabhängigen Faktoren, $\sin (2\pi /\lambda \cdot X)$ und $\cos (2\pi /\lambda \cdot X)$, sind unabhängig vom Gangunterschied, der Gangunterschied wirkt sich nur auf die jeweiligen Amplitude jedes der beiden Terme aus.
b) weiter unten werden wir sehen, dass sich der zweite Term durch Interferenz mit den anderen Komponenten des Streulichtes auslöscht.

Wir gehen davon aus, dass $|h_j|\ll \lambda$ und somit $q|h_j|\ll 2\pi$ und vereinfachen die o. g. Gleichung, indem wir die beiden trigonometrischen Funktionen von $h_j$durch ihre Reihenentwicklungen ersetzen.

$E_j(X)=$

${\sigma }_j\cdot (1-\frac{1}{2}{q}^2{h_j}^2)\cdot \sin (\frac{2\pi }{\lambda }\cdot X)+{\sigma }_j\cdot (q\cdot h_j)\cdot \cos (\frac{2\pi }{\lambda }\cdot X)=$$({\sigma }_j-\frac{1}{2}{q}^2\cdot {\sigma }_j\cdot {h_j}^2)\cdot \sin (\frac{2\pi }{\lambda }\cdot X)+{\sigma }_j\cdot h_j\cdot q\cdot \cos (\frac{2\pi }{\lambda }\cdot X)(34)$

Das Makromolekül besteht nun aus einer großen Zahl an Streuzentren. Wir addieren alle gestreuten Strahlen auf und erhalten.

$\sum E_j(X)=$

$(\sum {\sigma }_j-\frac{1}{2}{q}^2\sum {\sigma }_j\cdot {h_j}^2)\cdot \sin (\frac{2\pi }{\lambda }\cdot X)+\underset{=0}{\underbrace{\sum {\sigma }_j\cdot h_j}}\cdot q\cdot \cos (\frac{2\pi }{\lambda }\cdot X)=$

$(\sum {\sigma }_j-\frac{1}{2}{q}^2\sum {\sigma }_j\cdot {h_j}^2)\cdot \sin \left(\frac{2\pi }{\lambda }X\right)(35)$

Referenzpunkt unserer Betrachtungen ist der Schwerpunkt. Ziehen wir eine beliebige Ebene durch den Schwerpunkt eines Objektes, so ist die Summe von (Masse eines Objektteils x Abstand des Objektteils zu diese Ebene) gleich null. Folglich ist die Summe im zweiten Term und somit der gesamte zweite Term der obigen Gleichung gleich Null. Es bleibt nur der erste Term.
Teilen wir dies durch die Welle, die man bekäme, wenn alle Streuzentren im Schwerpunkt lägen $E^{*}=\mathrm{\Sigma }{\sigma }_j\cdot \sin (2\pi /\lambda \cdot X)$ erhält man:

$\frac{E}{E^{*}}=1-\frac{1}{2}{q}^2\frac{\sum {\sigma }_j\cdot {h_j}^2}{\sum {\sigma }_j}(36)$

Die Intensität der Strahlung ist proportional zum Quadrat der Amplitude. Somit erhalten wir:

$\frac{I}{I^{*}}={\left(\frac{E}{E^{*}}\right)}^2=1-2\cdot \frac{1}{2}{q}^2\frac{\sum {\sigma }_j\cdot {h_j}^2}{\sum {\sigma }_j}+{\left(\frac{1}{2}{q}^2\frac{\sum {\sigma }_j\cdot {h_j}^2}{\sum {\sigma }_j}\right)}^2$$\approx 1-q^2\frac{\sum {\sigma }_j\cdot {h_j}^2}{\sum {\sigma }_j}(37)$

$h_j$ hängt allerdings von der Orientierung des Makromoleküls ab. Das Licht, das der Detektor empfängt, stammt von vielen Makromolekülen, die zufällig im Raum verteilt und zufällig orientiert sind. Bei Licht, das aus vielen zufällig verteilten Lichtquellen stammt, ergibt sich die Gesamtintensität aus der Summe der Einzelintensitäten. Wir erhalten somit die mittlere Streuintensität, in dem wir ${h_j}^2$ in der obigen Gleichung durch ein gewichtetes Mittel ${h_j}^2\to ⟨{h_j}^2⟩$ ersetzen. Das Streuzentrum $\mathrm{I}$ liegt auf einer Hohlkugel um den Schwerpunkt mit Radius $r_j$  – überall auf dieser Hohlkugel mit gleicher Wahrscheinlichkeitsdichte. Die Linie $\overline{\mathrm{B}\mathrm{I}}$ symbolisiert die Mantelfläche einer Kugelschicht der Höhe $\mathrm{d}{h}_j$. Der Flächeninhalt dieser Mantelfläche hängt von $r_j$ und $\mathrm{d}{h}_j$, nicht jedoch von $h_j$ ab und beträgt $2\pi \cdot r_j\cdot \mathrm{d}{h}_j$. Wir erhalten somit das gewünschte gewichtete Mittel aus folgendem Integral:

$⟨{h_j}^2⟩=\frac{\underset{h_j=-r_j}{\overset{r_j}{\int }}2\pi \cdot r_j\cdot {h_j}^2\mathrm{d}{h}_j}{\underset{h_j=-r_j}{\overset{r_j}{\int }}2\pi \cdot r_j\mathrm{d}{h}_j}=$$\frac{\underset{h_j=-r_j}{\overset{r_j}{\int }}{h_j}^2\mathrm{d}{h}_j}{\underset{h_j=-r_j}{\overset{r_j}{\int }}\mathrm{d}{h}_j}=$$\frac{\frac{{r_j}^3}{3}-\frac{-{r_j}^3}{3}}{r_j-(-r_j)}=$$\frac{1}{3}{r_j}^2(38)$

Setzen wir dies anstelle von $h_j$ in Gleichung (37) ein erhalten wir:

$\frac{I}{I^{*}}\approx 1-q^2\frac{\sum {\sigma }_j\cdot ⟨{h_j}^2⟩}{\sum {\sigma }_j}$$=1-\frac{1}{3}{q}^2\frac{\sum {\sigma }_j\cdot {r_j}^2}{\sum {\sigma }_j}=$$1-\frac{1}{3}\cdot q^2\cdot R_g^2(39)$

Hierbei bezeichnen wir

$R_g^2=\frac{\sum {\sigma }_j\cdot {r_j}^2}{\sum {\sigma }_j}(40)$

als Streumassenradius.
Betrachten wir unser Makromolekül nicht als ein Objekt, das aus individuellen Wiederholungseinheiten zusammengesetzt ist, sondern als ein Kontinuum mit einer ortsabhängigen Dichte, $c_j$, so können wir ersetzen ${\sigma }_j\to c_j\cdot \mathrm{d}{V}_j$ und die Summen in Gleichung (40) in Integrale umwandeln und erhalten :
in kartesischen Koordinaten

$R_g^2=\frac{\underset{x=-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{y=-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{z=-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(x^2+y^2+z^2)\cdot c(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z}{\underset{x=-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{y=-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{z=-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}c(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z}(41)$

bzw. in Kugelkoordinaten:

$=\frac{\underset{r=0}{\overset{\mathrm{\infty }}{\int }}\underset{\vartheta =0}{\overset{\pi }{\int }}\underset{\phi =0}{\overset{2\pi }{\int }}{r}^2\cdot c(\vartheta ,\phi ,r)\cdot r\sin \vartheta \mathrm{d}\phi r\mathrm{d}\vartheta \mathrm{d}r}{\underset{r=0}{\overset{\mathrm{\infty }}{\int }}\underset{\vartheta =0}{\overset{\pi }{\int }}\underset{\phi =0}{\overset{2\pi }{\int }}c(\vartheta ,\phi ,r)\cdot r\sin \vartheta \mathrm{d}\phi r\mathrm{d}\vartheta \mathrm{d}r}(42)$

Bei einem kugelsymmetrischen Objekt ist die Massendichte $c(r)$ nur noch eine Funktion des Abstandes vom Schwerpunkt, d. h. die inneren Integrale ergeben $\int \int r\sin \vartheta \mathrm{d}\phi r\mathrm{d}\vartheta =4\pi r^2$ und der Ausdruck vereinfacht sich zu:

$R_g^2=\frac{\underset{r=0}{\overset{\mathrm{\infty }}{\int }}{r}^2\cdot c(r)4\pi r^2\mathrm{d}r}{\underset{r=0}{\overset{\mathrm{\infty }}{\int }}c(r)4\pi r^2\mathrm{d}r}(43)$

Der Streumassenradius ('Radius' bezeichnet hier den Abstand zum Schwerpunkt) ist nicht identisch mit dem Trägheitsradius in der Mechanik ('Radius' bedeutet dort Abstand zur Trägheitsachse).

Bei der Interpretation von $R_g^2$ sollte man sich vergegenwärtigen, dass in die Berechnung von $R_g^2$ das 'gesamte Volumen' des Objektes und nicht nur die 'äußeren Begrenzungen' eingehen, $R_g^2$ also i. d. R. kleiner ist als die weiteste Strecke, die man in das Molekül bzw. den Partikel hineinzeichnen kann und ebenfalls meist kleiner ist als der hydrodynamische Radius.

Für eine Kugel homogener Dichte mit Radius r gilt: $\sqrt{R_g^2}=\sqrt{3/5}\cdot r$.

Für einen dünnen Stab der Länge L gilt: $\sqrt{R_g^2}=\sqrt{1/3}\cdot L/2$.

Für ein statistisches Knäul aus einer frei beweglichen Kette aus N frei verknüpften, miteinander nicht wechselwirkenden Wiederholungseinheiten der Länge a gilt: $\sqrt{R_g^2}=\sqrt{N/6}\cdot a$

Zusammenführung der Effekte durch Konzentrationsfluktuationen und Interferenz

Für den nächsten Schritt benötigen wir den Kehrwert von Gleichung (39). $q^2\cdot R_g^2$ ist deutlich kleiner als 1. Für $\delta \ll 1$ gilt $1/(1\pm \delta )\approx 1\mp \delta$ somit gilt:

$\frac{I^{*}}{I}\approx 1+\frac{1}{3}\cdot q^2\cdot R_g^2(45)$

Gleichung (29) wurde unter der Annahme entwickelt, dass es zu keiner Abschwächung durch Interferenz kommt, nun berücksichtigen wir die Interferenz, indem wir den ersten Term von Gleichung (29) mit Gleichung (45) multiplizieren (sowohl in Gleichung (29) als auch in Gleichung (45) steht die Intensität des Streulichtes links vom Gleichheitszeichen im Nenner) und erhalten:

$\frac{K\cdot c}{\mathrm{\Delta }R(\theta ,c)}=\frac{1}{M_w}(1+\frac{1}{3}{q}^2{R}_g^2+\dots )+2A_{2}c+\dots (46)$

Die oben stehende Ableitung berücksichtigt nur die Abschwächung des Streulichtes durch Interferenz aufgrund der Größe und Form des Makromoleküls. Wir könnten auch Interferenzerscheinungen aufgrund Form und Größe der Konzentrationsfluktuationen berücksichtigen. In der Polymeranalytik konzentrieren wir uns jedoch auf die beiden folgenden Grenzfälle: (i) unendliche Verdünnung: hier können wir nicht ideale Effekte in der Thermodynamik vernachlässigen und benötigen die Beschreibung über Konzentrationsfluktuationen nicht. (ii) unendlich kleiner Streuwinkel – hier ist der Gangunterschied aller gestreuten Wellen gleich $0$ und wir können Abschwächung durch Interferenz ungeachtet ihrer Ursache vernachlässigen. Die unten erläuterte Auswertung über den Zimm-Plot extrapoliert genau zu diesen beiden Grenzfällen. Wird Lichtstreuung hingegen angewendet, um kritische Phänomene in Mischungen kleiner Moleküle zu untersuchen, werden Interferenzen aufgrund der Größe der Konzentrationsfluktuationen i. d. R. berücksichtigt.

Auswertung

Zimm plot

Gleichung (46) ergibt eine 3-dimensionale Beziehung zwischen $\mathrm{\Delta }R(\theta ,c)$, $c$ und $q$.

Zimm-Plot

Wir könnten:

• die gesuchten Parameter mittels des Levenberg-Marquardt-Algorithmus numerisch ermitteln (hierüber würden wir auch höhere Virialkoeffizienten erhalten)

oder

• $K\cdot c/\mathrm{\Delta }R(\theta ,c)$ gegen $c$ [ gegen $q^2$ ] auftragen und erhielten mehrere Kurvenscharen (jede bei einem anderen $q$ [einem anderen c ] gemessen)
• jede dieser Kurven gegen $c=0$ [ gegen $q^2=0$ ] extrapolieren und erhielten so Werte für $\mathrm{\Delta }R(\theta ,c=0)$ [ für $\mathrm{\Delta }R(\theta =0,c)$ ]
• Auftragung dieser extrapolieren Werte versus $q^2$ [ versus c ]ergäbe eine Gerade mit der Steigung $R_g^2/(3\cdot M_w)$ [ mit der Steigung $2A_2$]
• Extrapolation auf $q^2=0$ [auf $c=0$] ergäbe $1/M_w$.

Automatisierte Auswertungen gehen in der Regel nach einem der beiden o. g. mathematischen Methoden vor.

Eine besonders elegante graphischer Auswertung, in der die o. g. doppelte Extrapolation in einem Diagramm erfolgt, ist der Zimm-Plott:

• wir wählen eine mehr oder minder beliebige Konstante $k$ mit der Dimension 1/(Länge² Konzentration)
• wir tragen von allen unseren Messwerten $(\theta ,c,\mathrm{\Delta }R(\theta ,c))$ in einem zweidimensionalen Diagramm $K\cdot c/\mathrm{\Delta }R(\theta ,c)$ (Ordinate) versus $q^2+k\cdot c$ (Abszisse) auf ($\bullet$).

• wir verbinden jeweils die Schar der Punkte, die alle beim gleichen Streuwinkel aufgenommen wurden, mit je einer Linie ( ^____ ) und führen jede dieser Linien nach links weiter ( ^...... )
• auf jeder dieser Linien zeichnen wir ausgehend von dem Punkt, der zur niedrigsten vermessenen Konzentration, $c_{\text{min}}$, gehört, in einem Abstand von $-k\cdot c_{\text{min}}$ einen weiteren Punkt ein ($◼$). Dieser entspricht der Extrapolation auf $\underset{c\to 0}{\lim }\mathrm{\Delta }R(\theta ,c)$
• wir verbinden diese extrapolierten Punkte mit einer Linie und verlängern diese bis zum Schnittpunkt mit der Ordinate ( ----- ).
• die Steigung dieser Linie entspricht $R_g^2/(3\cdot M_w)$
• diese Linie schneidet die Ordinate bei $\underset{q\to 0}{\lim }\underset{c\to 0}{\lim }(K\cdot c/\mathrm{\Delta }R(\theta ,c))=1/M_w$
• wir verbinden jeweils die Schar der Punkte, die alle bei der gleichen Konzentration aufgenommen wurden, mit je einer Linie ( ^____ ) und führen jede dieser Linien nach links weiter ( ^...... )
• auf jeder dieser Linien zeichnen wir ausgehend von dem Punkt, der zum niedrigsten vermessenen Streuvektor, $q_{\text{min}}$, gehört, in einem Abstand von $-q_{\text{min}}^2$ einen weiteren Punkt ein ($▴$). Dieser entspricht der Extrapolation auf $\underset{q\to 0}{\lim }R(\theta ,c)$
• wir verbinden diese extrapolierten Punkte mit einer Linie und verlängern diese bis zum Schnittpunkt mit der Ordinate ( ----- ).
• die Steigung dieser Linie entspricht $2A_2/k$
• diese Linie schneidet die Ordinate ebenfalls bei $\underset{c\to 0}{\lim }\underset{q\to 0}{\lim }(K\cdot c/\mathrm{\Delta }R(\theta ,c))=1/M_w$

Guinier plot

Sind wir nur am Streumassenradius, $R_g^2$, interessiert, so ist eine Extrapolation $c\to 0$ nicht notwendig. Üblicherweise bestimmt man die Winkelabhängigkeit der Streuintensität für nur eine Konzentration und trägt $\ln (\mathrm{\Delta }R(\theta ,c)/\mathrm{\Delta }R({\theta }_{\text{min}},c))$ versus $q^2$ auf. Für $\delta \ll 1$ $\ln (1\pm \delta )\approx 1\pm \delta$. Somit ergibt diese Auftragung in dem Bereich $q^2\cdot R_g^2\ll 1$ eine Gerade mit Steigung $-(1/3)R_g^2$