NLC-Weite

Die NLC-Weite ist ein Begriff aus der Graphentheorie und weist jedem ungerichteten Graphen eine natürliche Zahl zu. Auf Graphen mit beschränkter NLC-Weite lassen sich bestimmte schwere Probleme wie zum Beispiel MAX-CUT oder das Hamiltonkreisproblem in polynomieller Zeit lösen.

Definition

Der Begriff der NLC-Weite wurde von 1994 von Wanke eingeführt. Für die Definition der NLC-Weite ist der Begriff des k-markierten Graphen wichtig:

k-markierter Graph

• Für ein  $k\in \mathbb{N}$ sei $[k]:=\{1,\dots ,k\}$
• Ein k-markierter Graph $G=(V_G,E_G,la{b}_G)$ ist ein Graph $(V_G,E_G)$, dessen Knoten mit einer Markierungsabbildung $la{b}_G:V_G\to [k]$ markiert werden
• Ein Graph mit genau einem mit $i\in [k]$ markierten Knoten wird mit ${\bullet }_i$ bezeichnet

Definition

Die NLC-Weite eines k-markierten Graphen $G$ ist die kleinste natürliche Zahl $k,$ sodass $G$ in der Graphklasse $NL{C}_k$ liegt.

Dabei ist $NL{C}_k$ wie folgt rekursiv definiert:

1. Der $k$-markierte Graph ${\bullet }_i$ ist für ein $i\in [k]$ in $NL{C}_k$
2. Seien $G=(V_G,E_G,la{b}_G)$ und $J=(V_J,E_J,la{b}_J)$ in $NL{C}_k$. Weiterhin seien $G$ und $J$ knotendisjunkt und $S\subseteq [k{]}^2$ eine Relation. Dann ist auch der $k$-markierte Graph

   $G{\times }_{S}J=(V^{\prime },E^{\prime },la{b}^{\prime })$

   in $NL{C}_k$, mit

   $V^{\prime }=V_G\cup V_J$,

   $E^{\prime }=E_G\cup E_J\cup \{\{u,v\}|u\in V_G,v\in V_J,(la{b}_G(u),la{b}_J(v))\in S\}$ und

   $la{b}^{\prime }(u)=\{\begin{array}{cc}la{b}_G(u),& \text{falls }u\in V_G\\ la{b}_J(u),& \text{falls }u\in V_J\end{array}$

   für alle $u\in V^{\prime }$.

3. Seien $G=(V_G,E_G,la{b}_G)\in NL{C}_k$ ein $k$-markierter Graph und $R:[k]\to [k]$ eine totale Funktion. Dann ist auch der $k$-markierte Graph

   ${\circ }_R(G)=(V_G,E_G,la{b}^{\prime })$

   in $NL{C}_k$ mit $la{b}^{\prime }(u)=R(lab(u))\mathrm{\forall }u\in V_G$.

Beispiel

Die nachfolgende Tabelle demonstriert die Konstruktion des "Haus vom Nikolaus"-Graphen mithilfe der oben definierten Operationen:

NLC-Operation	Darstellung des Graphen
$G_1={\bullet }_1{\times }_{\{(1,2)\}}{\bullet }_2$
$G_2={\bullet }_3{\times }_{\{(3,4)\}}{\bullet }_4$
$G_3=G_1{\times }_{\{(1,3),(1,4),(2,3),(2,4)\}}{G}_2$
$G_4={\circ }_{\{(1,1),(2,1),(3,3),(4,3)\}}(G_3)$
$G_{Nikolaus}=G_4{\times }_{\{(3,2)\}}{\bullet }_2$

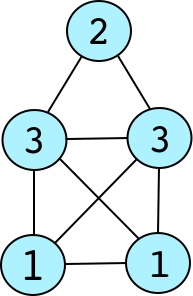
Es gilt somit $G_{Nikolaus}\in NL{C}_4$. $G_{Nikolaus}$ hat weiterhin eine NLC-Weite von 1, da $G_{Nikolaus}$ ein Co-Graph ist.

NLC-Weite spezieller Graphklassen

Die NLC-Weiten der folgenden Graphklassen lassen sich wie folgt nach oben abschätzen:

• Jeder Co-Graph hat eine NLC-Weite von 1
• Bäume haben eine NLC-Weite von höchstens 3
• Kreise haben eine NLC-Weite von höchstens 4

Zusammenhang zur Cliquenweite

Für jeden ungerichteten Graphen $G$ mit NLC-Weite $nlcw(G)$ und Cliquenweite $cw(G)$ gilt:

$nlcw(G)\le cw(G)\le 2\cdot nlcw(G).$

Literatur

• Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme, Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-642-04499-1