Co-Graph

In der Informatik ist ein Co-Graph ein ungerichteter Graph $G=(V,E)$, welcher sich mit bestimmten elementaren Operationen konstruieren lässt. Auf Co-Graphen lassen sich viele schwere Probleme wie z. B. CLIQUE und das damit eng verwandte UNABHÄNGIGE MENGE sowie KNOTENÜBERDECKUNG in Linearzeit lösen.

Definition

Abbildung eines Co-Graphen. Wie man sieht, ist kein induzierter$P_4$ enthalten.

Dieser Graph ist kein Co-Graph, da ein induzierter$P_4$ enthalten ist.

Ein Graph $G=(V,E)$ ist ein Co-Graph, falls er sich mit den folgenden drei Operationen konstruieren lässt:

1. Der Graph $K_1$ mit genau einem Knoten ist ein Co-Graph (in Zeichen $K_1=\bullet$).
2. Für zwei Co-Graphen $G_1=(V_1,E_1)$ und $G_2=(V_2,E_2)$ ist die disjunkte Vereinigung $G_1\cup G_2:=(V_1\cup V_2,E_1\cup E_2)$ ein Co-Graph.
3. Für zwei Co-Graphen $G_1=(V_1,E_1)$ und $G_2=(V_2,E_2)$ ist die disjunkte Summe $G_1\times G_2:=(V_1\cup V_2,E_1\cup E_2\cup \{\{u,v\}|u\in V_1,v\in V_2\})$ ein Co-Graph.

Äquivalente Charakterisierungen

Für einen Graphen $G$ sind folgende Aussagen äquivalent:

• $G$ ist ein Co-Graph.
• $G$ enthält keinen induzierten $P_4$, wobei $P_4$ den ungerichteten Weg mit vier Knoten bezeichnet.
• Der Komplementgraph jedes zusammenhängenden induzierten Teilgraphen von $G$ mit mindestens zwei Knoten ist unzusammenhängend.
• $G$ lässt sich mit den folgenden drei Regeln konstruieren:

1. Jeder Graph $K_1$ mit genau einem Knoten ist ein Co-Graph.
2. Für zwei Co-Graphen $G_1$ und $G_2$ ist die disjunkte Vereinigung $G_1\cup G_2$ ein Co-Graph.
3. Für einen Co-Graphen $G$ ist auch der Komplementgraph $\overline{G}$ ein Co-Graph.

Co-Baum

Um auf Co-Graphen effizient schwere Probleme lösen zu können, kann man sie mithilfe von Co-Bäumen darstellen. Ein Co-Baum ist ein binärer Baum, dessen Blätter mit $\bullet$ und dessen innere Knoten mit $\cup$ bzw. $\times$ markiert sind.

Ein Co-Baum $T$ ist wie folgt definiert:

1. Der Co-Baum $T$ zu dem Co-Graphen $G=\bullet$ ist der Baum mit einem Knoten, der mit $\bullet$ markiert ist.
2. Seien $G_1$ und $G_2$ Co-Graphen mit den Co-Bäumen $T_1$ und $T_2$. Der Co-Baum $T$ zu der disjunkten Vereinigung von $G_1$ und $G_2$ besteht aus einem mit $\cup$ markierten Wurzelknoten mit den Kindern $T_1$ und $T_2$.
3. Seien $G_1$ und $G_2$ Co-Graphen mit den Co-Bäumen $T_1$ und $T_2$. Der Co-Baum $T$ zu der disjunkten Summe von $G_1$ und $G_2$ besteht aus einem mit $\times$ markierten Wurzelknoten mit den Kindern $T_1$ und $T_2$.

Beispiel

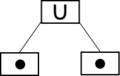
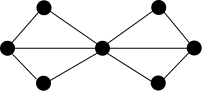
Das nachfolgende Beispiel skizziert die Konstruktion eines Co-Graphen $G_5$ mit zugehörigem Co-Baum $T_5$:

Co-Graph	Darstellung des Co-Graphen	Darstellung des Co-Baumes	Co-Baum
$G_1=\bullet$			$T_1$
$G_2=G_1\cup G_1$			$T_2$
$G_3=G_1\times G_2$			$T_3$
$G_4=G_3\cup G_3$			$T_4$
$G_5=G_1\times G_4$			$T_5$

Weitere Beispiele für Co-Graphen sind vollständige Graphen und vollständig unzusammenhängende Graphen.

Eigenschaften von Co-Graphen

Es ist leicht einzusehen, dass Co-Graphen unter Komplementbildung abgeschlossen sind. Um den Komplementgraphen zu erzeugen, müssen im zugehörigen Co-Baum lediglich die Operationen $\cup$ und $\times$ vertauscht werden.

Weiterhin ist die Menge der Co-Graphen unter Bildung induzierter Teilgraphen abgeschlossen.

Ebenfalls ist bekannt, dass jeder Co-Graph ein perfekter Graph ist.

Anwendung in der Algorithmik

Einige schwere Graphenprobleme lassen sich auf Co-Graphen in Linearzeit lösen. Dazu zählen u. a. die Probleme UNABHÄNGIGE MENGE, CLIQUE und KNOTENÜBERDECKUNG.

Mithilfe von dynamischer Programmierung auf den zugehörigen Co-Bäumen lassen sich einfach und elegant Lösungen für die genannten Probleme finden.

Literatur

• Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme, Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-642-04499-1