Monade (Kategorientheorie)

Eine Monade ist im mathematischen Teilgebiet der Kategorientheorie eine Struktur, die gewisse formale Ähnlichkeit mit den Monoiden der Algebra aufweist.

Definition

Eine Monade ist ein Tripel $(T,\eta ,\mu )$ aus

• einem Funktor $T$ von einer Kategorie $𝒞$ in sich selbst, das heißt

  $T:𝒞\to 𝒞$

• einer natürlichen Transformation $\eta :1_{𝒞}\to T$ (dabei steht $1_{𝒞}$ für den Identitätsfunktor $𝒞\to 𝒞$)
• einer natürlichen Transformation $\mu :T^2\to T$ (dabei steht $T^2$ für $T\circ T$),

so dass die folgenden Bedingungen, die man auch die Axiome der Monade nennt, erfüllt sind:

• $\mu \circ T\mu =\mu \circ \mu T$, das heißt das folgende Diagramm kommutiert:

• $\mu \circ \eta T=\mu \circ T\eta =1$, das heißt das folgende Diagramm kommutiert:

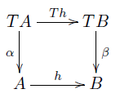
Explizit bedeutet die Kommutativität der Diagramme, dass für jedes Objekt $X$ in $𝒞$ die beiden Diagramme

  und  

kommutieren. Dabei sind $T\mu$ und $\mu T$ die durch $(T\mu {)}_X:=T({\mu }_X)$ und $(\mu T{)}_X:={\mu }_{T(X)}$ definierten natürlichen Transformationen, entsprechendes gilt für $T\eta$ und $\eta T$. Die natürlichen Transformationen $\eta$ und $\mu$ nennt man auch Einheit und Multiplikation der Monade.

Beispiel Listen

Ein Beispiel für eine Monade sind Listen. Es bezeichne $[x_1,\dots ,x_n]$ die Liste mit den Elementen $x_1$ bis $x_n$, wobei mit $n=0$ auch die leere Liste zugelassen ist. Listen sind Tupel, die wir hier der Übersichtlichkeit wegen mit eckigen Klammen schreiben. Das folgende Tripel $(T,\eta ,\mu )$ ist eine Monade in der Kategorie der Mengen $𝐒𝐞𝐭$:

Der Listen-Funktor

• Für ein Objekt $X$ aus $𝐒𝐞𝐭$, das heißt für eine Menge $X$, sei $T(X)=\{[x_1,\dots ,x_n]\mid n\in \mathbb{N},x_1,\dots ,x_n\in X\}$ die Menge aller endlichen Listen, deren Elemente aus $X$ kommen.
• Für eine Abbildung $f:X\to Y$ zwischen zwei Mengen sei $T(f):T(X)\to T(Y)$ zwischen den Listenmengen durch $T(f)([x_1,\dots ,x_n])=[f(x_1),\dots ,f(x_n)]$ definiert.

Einheit und Multiplikation

• Die Einheit $\eta$ sei definiert durch ${\eta }_X(x)=[x]$, das ist die Konstruktion einelementiger Listen.
• Die Multiplikation ist die Konkatenation von Listen: ${\mu }_X([l_1,\dots ,l_n])=l_1\cdots l_n$, also ${\mu }_X([[x_{11},\dots ,x_{1m_1}],\dots ,[x_{n1},\dots ,x_{n{m}_n}]])=[x_{11},\dots ,x_{1m_1},\dots ,x_{n1},\dots ,x_{n{m}_n}]$ – dies ist gewissermaßen das (einstufige) Zusammenfügen einer Liste von Listen zu einer Liste.

Diese Daten erfüllen die Definition der Monade.

• Die Gleichung $\mu \circ T\mu =\mu \circ \mu T$ bedeutet für eine Liste von Listen von Listen $l\in T(T(T(X)))$, dass ${\mu }_X(T({\mu }_X)(l))={\mu }_X({\mu }_{T(X)}(l))$, das heißt, dass es bei mehrfach verschachtelten Listen egal ist, ob diese von innen oder von außen beginnend zu einer zusammengefügt werden. Betrachte zum Beispiel $l=[[[x,y],[x]],[[x,y,z],[x,x]]]$, wobei $x,y,z\in X$ seien. Das ist die Liste der beiden Listen von Listen $[[x,y],[x]]$ und $[[x,y,z],[x,x]]$, die ihrerseits aus den Listen $[x,y]$ und $[x]$ bzw. $[x,y,z]$ und $[x,x]$ bestehen. Dann ist

${\mu }_X(T({\mu }_X)(l))={\mu }_X([[x,y,x],[x,y,z,x,x]])=[x,y,x,x,y,z,x,x]$ und

${\mu }_X({\mu }_{T(X)}(l))={\mu }_X([[x,y],[x],[x,y,z],[x,x]])=[x,y,x,x,y,z,x,x]$.

• Das zweite Axiom besagt in diesem Beispiel, dass jede Liste durch Zusammenfügen einelementiger Listen entsteht:

${\mu }_X({\eta }_{T(X)}([x_1,\dots ,x_n]))={\mu }_X([[x_1,\dots ,x_n]])=[x_1,\dots ,x_n]={\mu }_X([[x_1],\dots ,[x_n]])={\mu }_X(T({\eta }_X)([x_1,\dots ,x_n]))$.

In einer algebraischen Sichtweise ist $T(X)$ die unterliegende Menge des freien Monoids über $X$. Die Einheit ${\eta }_X$ bettet das Erzeugendensystem in den Monoid ein, die Multiplikation ${\mu }_X$ ist die Monoidmultiplikation.

Eilenberg-Moore-Algebren

Ist $(T:𝒞\to 𝒞,\eta ,\mu )$ eine Monade, so ist ein Paar $(A,\alpha :T(A)\to A)$ eine Eilenberg-Moore-Algebra (auch einfach nur Algebra genannt) für diese Monade, wenn die Gleichungen

• $\alpha \circ {\eta }_A=1_A$ und
• $\alpha \circ {\mu }_A=\alpha \circ T(\alpha )$

gelten, das heißt, wenn die folgenden beiden Diagramme kommutieren:

Ein Homomorphismus von $(A,\alpha )$ nach $(B,\beta )$ ist ein Pfeil $h:A\to B$ in $K$ mit $h\circ \alpha =\beta \circ T(h)$, das heißt, dass nachstehendes Diagramm kommutiert:

Für beliebige Objekte $X$ aus $𝒞$ ist daher z. B. $(T(X),{\mu }_X)$ eine Algebra, und ${\mu }_X$ ist ein Homomorphismus von $(T(T(X)),{\mu }_{T(X)})$ nach $(T(X),{\mu }_X)$. Im obigen Beispiel der Listen sind die Algebren $(A,\alpha :TA\to A)$ genau die Monoide $A$ und $\alpha$ multipliziert alle Elemente der Liste.

Die Eilenberg-Moore-Algebren zur Monade $T$ bilden mit den angegebenen Homomorphismen eine Kategorie, die man die Kategorie der $T$-Algebren nennt und mit ${𝒞}^T$ bezeichnet. Im Falle der Listen-Monade $T$ ist also ${𝐒𝐞𝐭}^T$ die Kategorie der Monoide.

Weitere Beispiele

Linearkombinationen

Es sei $K$ ein Körper. Legt man für Mengen $X$ fest, dass $L(X):=\{v:X\to K\mid v^{-1}(K\setminus \{0\})\text{ endlich}\}$ sei, also (eine Kodierung für) die Menge der formalen $K$-Linearkombinationen von Elementen von $X$, lässt sich $L$ als Objektabbildung eines Funktors $L:𝐒𝐞𝐭\to 𝐒𝐞𝐭$ auffassen, dessen Pfeilabbildung einer Funktion $f:X\to Y$ die Funktion $L(f):L(X)\to L(Y)$, mit $L(f)(v)(y):=\sum _{x\in f^{-1}(\{y\})}v(x)$, zuordnet. $L(X)$ trägt eine naheliegende Vektorraumstruktur: Für $\lambda \in K$ und $v\in L(X)$ ist $\lambda \cdot v$, definiert durch $(\lambda \cdot v)(x):=\lambda \cdot v(x)$, wieder Element von $L(X)$, und für $v,w\in L(X)$ ist $v+w$, definiert durch $(v+w)(x):=v(x)+w(x)$, ebenfalls wieder Element von $L(X)$.

Der Funktor $L$ wird zusammen mit den Festlegungen

• ${\eta }_X(x)(y):=\{\begin{array}{cc}1& x=y\\ 0& \text{sonst}\end{array}$
• ${\mu }_X(l):=\sum _{v\in l^{-1}(K\setminus \{0\})}l(v)\cdot v$

(hier verwenden wir der Übersichtlichkeit halber $+$ und $\cdot$ aus dem vorangegangenen Satz)

zu einer Monade $𝐒𝐞𝐭\to 𝐒𝐞𝐭$. ${\mu }_X$ berechnet dabei auf naheliegende Weise aus einer Linearkombination von Linearkombinationen von Elementen von $X$ die entsprechende Zusammenfassung als Linearkombination von Elementen von $X$.

Die Algebren der Monade $(L,\eta ,\mu )$ sind gerade $K$-Vektorräume, in der zur Monade gehörenden Kleisli-Kategorie sind die Pfeile $X\to Y$ gerade (Mengen-indizierte) $X$-$Y$-Matrizen, die sich als Codes für lineare Abbildungen vom freien Vektorraum über $X$ zum freien Vektorraum über $Y$ auffassen lassen.

Dcpos

Der Endofunktor $\mathrm{I}\mathrm{d}\mathrm{l}:𝐏𝐨𝐬\to 𝐏𝐨𝐬$ auf der Kategorie der partiell geordneten Mengen und monotonen Abbildungen ordne jedem $(A,\le )$ die partiell geordnete Menge $(\mathrm{I}\mathrm{d}\mathrm{l}(A),\subseteq )$ der Ordnungsideale in $A$ zu. Seine Wirkung auf monotonen Abbildungen $f:A\to B$ sei $\mathrm{I}\mathrm{d}\mathrm{l}(f):I\mapsto \downarrow \{f(a)\mid a\in I\}$. Für eine partiell geordnete Menge $X$ und eine Teilmenge $U\subseteq X$ ist hierbei $\downarrow U:=\{x\in X\mid \mathrm{\exists }u\in U.x\le u\}$.

Die Abbildungsfamilien ${\mu }_A:ℐ\mapsto \bigcup ℐ$ und ${\eta }_A:a\mapsto \downarrow \{a\}$ ergänzen den Funktor $\mathrm{I}\mathrm{d}\mathrm{l}$ zu einer Monade.

Die Strukturabbildung $\alpha$ einer $\mathrm{I}\mathrm{d}\mathrm{l}$-Algebra $(A,\alpha :\mathrm{I}\mathrm{d}\mathrm{l}(A)\to A)$ ist nun gerade $I\mapsto \sup I$. Jedes Ideal in $A$ (und somit jede gerichtete Teilmenge) hat also ein Supremum in $A$. Das heißt, eine $\mathrm{I}\mathrm{d}\mathrm{l}$-Algebra ist dasselbe wie eine Dcpo. Ein Homomorphismus von $\mathrm{I}\mathrm{d}\mathrm{l}$-Algebren ist eine Scott-stetige Abbildung.

Adjungierte Funktoren

Ist ein Funktor $F:𝒞\to 𝒟$ zu einem Funktor $G:𝒟\to 𝒞$ linksadjungiert, und sind

$\eta :1_{𝒞}\to GF$ bzw. $\epsilon :FG\to 1_{𝒟}$

Einheit bzw. Koeinheit der Adjunktion, so ist $(T,\eta ,\mu )$ mit

• $T=GF:𝒞\to 𝒞$
• $\mu =G\epsilon F,$ also ${\mu }_X=G({\epsilon }_{F(X)})$ für Objekte $X\in \mathrm{O}\mathrm{b}(𝒞)$

eine Monade.

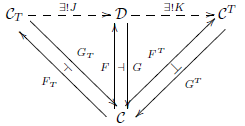
Dies ist im gewissen Sinn auch schon das einzige Beispiel, da jede Monade auf diese Weise entsteht, jedenfalls bis auf Isomorphie: Die Tripel $(𝒟,F,G)$ mit $F:𝒞\to 𝒟$, $G:𝒟\to 𝒞$, $GF=T$ und $F⊣G$ sind Objekte einer Kategorie $𝔄$. In dieser Kategorie ist ein Morphismus von $({𝒟}_1,F_1,G_1)$ nach $({𝒟}_2,F_2,G_2)$ ein Funktor $K:{𝒟}_1\to {𝒟}_2$, für den $K{F}_1=F_2$ und $G_{2}K=G_1$ gelten.

Anfangsobjekt in $𝔄$ ist $({𝒞}_T,F_T,G_T)$, wobei ${𝒞}_T$ die Kleisli-Kategorie zu $T$ ist. $F_{T}X:=X$, für $f\in 𝒞(X,Y)$ ist $F_T(f):={\eta }_Y\circ f$. $G_{T}X:=TX$, für $f\in {𝒞}_T(X,Y)$ ist $G_T(f):={\mu }_Y\circ T(f)$.

Endobjekt in $𝔄$ ist $({𝒞}^T,F^T,G^T)$ wobei ${𝒞}^T$ die Kategorie der Eilenberg-Moore-Algebren zu $T$ ist. $F^{T}X:=(TX,{\mu }_X)$, für $f\in 𝒞(X,Y)$ ist $F^T(f):=T(f)$. $G^T(X,\alpha ):=X$, $G^T(f):=f$.

Für eine vorgegebene Adjunktion $F⊣G$ gibt es daher eindeutig existierende Funktoren $J$ und $K$ wie im nachfolgenden Diagramm, so dass die oben genannten Gleichungen bestehen, das heißt $J{F}_T=F$, $GJ=G_T$, $KF=F^T$ und $G^{T}K=G$

Den Funktor $K$ nennt man auch den Vergleichsfunktor, weil der die Kategorie $𝒟$ mit einer Kategorie von Algebren vergleicht. Man nennt die Adjunktion $F⊣G$ monadisch, wenn der Vergleichsfunktor eine Äquivalenz $𝒟\simeq {𝒞}^T$ ist. Man nennt einen Funktor $G$ monadisch, wenn es eine Linksadjungierte $F$ gibt, so dass die Adjunktion $F⊣G$ monadisch ist.

Anwendung in der Informatik

Monaden werden in der Informatik, besonders in funktionalen Programmiersprachen u. a. zur Abstraktion von Nebeneffekten verwendet. Es ist Haskell hervorzuheben, wo Monaden zur Integration von Ein- und Ausgabe in die sonst komplett von Seiteneffekten freie Sprache verwendet werden. Siehe dazu auch Monade (Informatik).

Weblinks

• Lektion zu Monaden
• You Could Have Invented Monads! (And Maybe You Already Have.)
• Mehrteiliger Videokurs für Mathematiker (englisch)