Differential (Mathematik)

Ein Differential (oder Differenzial) bezeichnet in der Analysis den linearen Anteil des Zuwachses einer Variablen oder einer Funktion und beschreibt einen unendlich kleinen Abschnitt auf der Achse eines Koordinatensystems. Historisch war der Begriff im 17. und 18. Jahrhundert der Kern der Entwicklung der Infinitesimalrechnung. Ab dem 19. Jahrhundert wurde die Analysis durch Augustin Louis Cauchy und Karl Weierstraß auf der Grundlage des Grenzwertbegriffes mathematisch korrekt neu aufgebaut, und der Begriff des Differentials verlor für die elementare Differential- und Integralrechnung an Bedeutung.

Besteht eine funktionale Abhängigkeit $y=f(x)$ mit einer differenzierbaren Funktion $f$, dann lautet der grundlegende Zusammenhang zwischen dem Differential $\mathrm{d}y$ der abhängigen Variablen und dem Differential $\mathrm{d}x$ der unabhängigen Variablen

$\mathrm{d}y=f^{\prime }(x)\mathrm{d}x$,

wobei $f^{\prime }(x)$ die Ableitung von $f$ an der Stelle $x$ bezeichnet. Anstelle von $\mathrm{d}y$ schreibt man auch $\mathrm{d}f(x)$ oder $\mathrm{d}{f}_x$. Diese Beziehung lässt sich mit Hilfe partieller Ableitungen auf Funktionen mehrerer Variablen verallgemeinern und führt dann auf den Begriff des totalen Differentials.

Differentiale werden heute in verschiedenen Anwendungen in unterschiedlicher Bedeutung und auch mit unterschiedlicher mathematischer Strenge verwendet. Die in Standardschreibweisen wie ${\int }_a^{b}f(x)\mathrm{d}x$ für Integrale oder $\frac{\mathrm{d}f}{\mathrm{d}x}$ für Ableitungen auftretenden Differentiale werden heutzutage üblicherweise als bloßer Notationsbestandteil ohne eigenständige Bedeutung angesehen.

Eine rigorose Definition liefert die in der Differentialgeometrie verwendete Theorie der Differentialformen, wo Differentiale als exakte 1-Formen interpretiert werden. Einen anders gearteten Zugang vermittelt die Nichtstandardanalysis, die den historischen Begriff der Infinitesimalzahl wieder aufgreift und im Sinne der modernen Mathematik präzisiert.

Einordnung

In seinen 1924 erstmals erschienenen „Vorlesungen über Differential- und Integralrechnung“ schreibt Richard Courant, dass die Idee des Differentials als unendlich kleine Größe keine Bedeutung habe und es deshalb nutzlos sei, die Ableitung als Quotient zweier solcher Quantitäten zu definieren, dass man aber trotzdem versuchen könne, den Ausdruck $\frac{\mathrm{d}y}{\mathrm{d}x}$ als tatsächlichen Quotienten zweier Quantitäten $\mathrm{d}y$ und $\mathrm{d}x$ zu definieren. Dafür definiere man zunächst $f^{\prime }(x)$ wie üblich als

$f^{\prime }(x):=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$

und betrachte dann für ein festes $x$ den Zuwachs $h=\mathrm{\Delta }x$ als eine unabhängige Variable. (Diese bezeichne man als $h=\mathrm{d}x$.) Dann definiere man $\mathrm{d}y=h{f}^{\prime }(x)$, womit man tautologisch $f^{\prime }(x)=\frac{\mathrm{d}y}{\mathrm{d}x}$ bekomme.

In modernerer Terminologie kann man das Differential in $x$ als lineare Abbildung vom Tangentialraum $T_xℝ\simeq ℝ$ in die reellen Zahlen auffassen. Dem „Tangentialvektor“ $h\in ℝ\simeq T_xℝ$ wird die reelle Zahl $h{f}^{\prime }(x)$ zugeordnet und diese lineare Abbildung ist per Definition das Differential $\mathrm{d}f(x)$. Also $\mathrm{d}f(x)(h)=f^{\prime }(x)h$ und insbesondere $\mathrm{d}x(x)(h)=h$, woraus sich tautologisch die Beziehung $f^{\prime }(x)=\frac{\mathrm{d}f(x)}{\mathrm{d}x(x)}$ ergibt.

Das Differential als linearisierter Zuwachs

Ist $f:ℝ\to ℝ$ eine reelle Funktion einer reellen Variablen, so bewirkt eine Änderung des Arguments um $\mathrm{\Delta }x$ von $x$ auf $x+\mathrm{\Delta }x$ eine Änderung des Funktionswertes von $y=f(x)$ auf $y+\mathrm{\Delta }y=f(x+\mathrm{\Delta }x)$; für den Zuwachs des Funktionswerts gilt also

$\mathrm{\Delta }y=f(x+\mathrm{\Delta }x)-f(x)$.

Ist beispielsweise $f$ eine (affin) lineare Funktion, also $y=f(x)=mx+b$, so folgt $\mathrm{\Delta }y=m\cdot \mathrm{\Delta }x$. Das heißt, der Zuwachs des Funktionswerts ist in diesem einfachen Fall direkt proportional zum Zuwachs des Arguments und das Verhältnis $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$ entspricht gerade der konstanten Steigung $m$ von $f$.

Datei:Dydx.PNG

Das Differential $\mathrm{d}y$ als linearer Anteil des Zuwachses $\mathrm{\Delta }y$

Bei Funktionen, deren Steigung nicht konstant ist, ist die Situation komplizierter. Ist $f$ an der Stelle $x$ differenzierbar, dann ist die Steigung dort gegeben durch die Ableitung $f^{\prime }(x)$, wobei diese als Grenzwert des Differenzenquotienten definiert ist:

$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$.

Betrachtet man nun für $\mathrm{\Delta }x\ne 0$ die Differenz zwischen dem Differenzenquotienten und der Ableitung

$\varphi (\mathrm{\Delta }x):=\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}-f^{\prime }(x)$,

so folgt für den Zuwachs des Funktionswertes

$\mathrm{\Delta }y=f^{\prime }(x)\cdot \mathrm{\Delta }x+\varphi (\mathrm{\Delta }x)\cdot \mathrm{\Delta }x$.

In dieser Darstellung wird $\mathrm{\Delta }y$ zerlegt in einen Anteil $f^{\prime }(x)\cdot \mathrm{\Delta }x$, der linear von $\mathrm{\Delta }x$ abhängt, und einen Rest, der von höherer als linearer Ordnung verschwindet, in dem Sinne, dass $\underset{h\to 0}{\lim }\varphi (h)=0$ gilt. Der lineare Anteil des Zuwachses, der deshalb für kleine Werte von $\mathrm{\Delta }x$ im Allgemeinen einen guten Näherungswert für $\mathrm{\Delta }y$ darstellt, wird Differential von $f$ genannt und mit $\mathrm{d}y$ bezeichnet.

Definition

Es sei $f:D\to ℝ$ eine Funktion mit Definitionsbereich $D\subseteq ℝ$. Ist $f$ an der Stelle $x\in D$ differenzierbar und $h\in ℝ$, dann heißt

$\mathrm{d}f(x)(h):=f^{\prime }(x)\cdot h$

das Differential von $f$ an der Stelle $x$ zum Argumentzuwachs $h$. Statt $h$ schreibt man häufig auch $\mathrm{d}x$. Gilt $y=f(x)$, so schreibt man auch $\mathrm{d}y$ anstelle von $\mathrm{d}f(x)$.

Für ein fest gewähltes $x$ ist das Differential $\mathrm{d}f(x)$ also eine lineare Funktion, die jedem Argument $h\in ℝ$ den Wert $f^{\prime }(x)h\in ℝ$ zuordnet.

Beispielsweise für die identische Funktion $\mathrm{i}\mathrm{d}:ℝ\to ℝ$, $\mathrm{i}\mathrm{d}(x)=x$ gilt also wegen ${\mathrm{i}\mathrm{d}}^{\prime }(x)=1$ die Gleichung $\mathrm{d}x=\mathrm{d}\mathrm{(}\mathrm{i}\mathrm{d}\mathrm{)}(x)=1\cdot h=h$ und somit in diesem Beispiel $\mathrm{d}y=\mathrm{d}x$.

Differentiale höherer Ordnung

Ist $f:D\to ℝ$ an der Stelle $x\in D\subseteq ℝ$ $n$-mal differenzierbar ($n\in \mathbb{N}$) und $\mathrm{d}x=h\in ℝ$, so heißt

${\mathrm{d}}^{n}y:={\mathrm{d}}^{n}f(x):=f^{(n)}(x)\mathrm{d}{x}^n$

das Differential $n$-ter Ordnung von $f$ an der Stelle $x$ zum Argumentzuwachs $h$. In diesem Produkt bezeichnet $f^{(n)}(x)$ die $n$-te Ableitung von $f$ an der Stelle $x$ und $\mathrm{d}{x}^n$ die $n$-te Potenz der Zahl $\mathrm{d}x$.

Die Bedeutung dieser Definition wird bei Courant wie folgt erklärt. Wenn man sich $h$ fest gewählt denkt, und zwar denselben Wert $h$ für verschiedene $x$, also $\mathrm{\Delta }x$ festgehalten, dann ist $\mathrm{d}y=h{f}^{\prime }(x)$ eine Funktion von $x$, von der man wieder das Differential ${\mathrm{d}}^{2}y=\mathrm{d}(h{f}^{\prime }(x))$ bilden kann (s. Abb.). Das Ergebnis ist das zweite Differential ${\mathrm{d}}^{2}y={\mathrm{d}}^{2}f(x)$, man erhält es, indem man in $h\{f^{\prime }(x+h)-f^{\prime }(x)\}$ (dem Zuwachs von $h{f}^{\prime }(x)$) den Term in Klammern durch seinen Linearteil $h{f}^{\prime \prime }(x)$ ersetzt, womit also ${\mathrm{d}}^{2}y=h^2{f}^{\prime \prime }(x)$ ist. Auf analoge Weise kann man die Definition von Differentialen höherer Ordnung motivieren. Es gilt dann entsprechend z. B. ${\mathrm{d}}^{3}y=h^3{f}^{‴}(x)$ und allgemein ${\mathrm{d}}^{n}y=h^n{f}^{(n)}(x)$.

Für ein fest gewähltes $x$ ist das Differential ${\mathrm{d}}^{n}f(x)$ also wieder eine (für $n>1$ nicht-lineare) Funktion, die jedem Argument $h\in ℝ$ den Wert $f^{(n)}(x)h^n\in ℝ$ zuordnet.

Rechenregeln

Unabhängig von der verwendeten Definition gelten für Differentiale die folgenden Rechenregeln. Im Folgenden bezeichnen $x$ die unabhängige Variable, $u,v,y,z$ abhängige Variablen beziehungsweise Funktionen und $c$ eine beliebige reelle Konstante. Die Ableitung von $y$ nach $x$ wird $\frac{\mathrm{d}y}{\mathrm{d}x}$ geschrieben. Dann ergeben sich die nachfolgenden Rechenregeln aus der Beziehung

$\mathrm{d}y=\frac{\mathrm{d}y}{\mathrm{d}x}\mathrm{d}x$

und den Ableitungsregeln. Die folgenden Rechenregeln für Differentiale von Funktionen $f:ℝ\to ℝ$ sind so zu verstehen, dass jeweils die nach Einsetzen der Argumente $dx=h\in ℝ$ erhaltenen Funktionen übereinstimmen sollen. Die Regel $\mathrm{d}(u+v)=\mathrm{d}u+\mathrm{d}v$ zum Beispiel besagt, dass man in jedem $x\in ℝ$ die Identität $\mathrm{d}(u+v)(x)=\mathrm{d}u(x)+\mathrm{d}v(x)$ hat und dies bedeutet nach Definition, dass für alle reellen Zahlen $h$ die Gleichung $\mathrm{(}u+v{)}^{\prime }(x)\cdot h=u^{\prime }(x)\cdot h+v^{\prime }(x)\cdot h$ gelten soll.

Konstante und konstanter Faktor

• $\mathrm{d}(c)=0$ und
• $\mathrm{d}(cy)=c\mathrm{d}y$

Addition und Subtraktion

• $\mathrm{d}(u+v)=\mathrm{d}u+\mathrm{d}v$ ; und
• $\mathrm{d}(u-v)=\mathrm{d}u-\mathrm{d}v$

Multiplikation

auch Produktregel genannt:

• $\mathrm{d}(uv)=v\mathrm{d}u+u\mathrm{d}v=(uv)(\frac{\mathrm{d}u}{u}+\frac{\mathrm{d}v}{v})$

Division

• $\mathrm{d}\left(\frac{u}{v}\right)=\frac{v\mathrm{d}u-u\mathrm{d}v}{v^2}=\left(\frac{u}{v}\right)(\frac{\mathrm{d}u}{u}-\frac{\mathrm{d}v}{v})$

Kettenregel

• Ist $z$ abhängig von $y$ und $y$ von $x$, also $\mathrm{d}z=\frac{\mathrm{d}z}{\mathrm{d}y}\mathrm{d}y$ und $\mathrm{d}y=\frac{\mathrm{d}y}{\mathrm{d}x}\mathrm{d}x$, dann gilt

$\mathrm{d}z=\frac{\mathrm{d}z}{\mathrm{d}y}\cdot \frac{\mathrm{d}y}{\mathrm{d}x}\mathrm{d}x$.

Beispiele

• Für $u=x^2$ und $v=\sin (x)$ gilt $\mathrm{d}u=2x\mathrm{d}x$ bzw. $\mathrm{d}v=\cos (x)\mathrm{d}x$. Es folgt

$\mathrm{d}(uv)=\mathrm{d}(x^2\sin (x))=x^2\cos (x)\mathrm{d}x+\sin (x)2x\mathrm{d}x$.

• Für $y=1+x^2$ und $z=\sqrt{y}$ gilt $\mathrm{d}y=2x\mathrm{d}x$ und $\mathrm{d}z=\frac{\mathrm{d}y}{2\sqrt{y}}$, also

$\mathrm{d}(\sqrt{1+x^2})=\mathrm{d}z=\frac{2x\mathrm{d}x}{2\sqrt{y}}=\frac{x}{z}\mathrm{d}x$.

Erweiterung und Varianten

Anstatt $\mathrm{d}$ finden sich folgende Symbole, die Differentiale bezeichnen:

• Mit $\partial$ (eingeführt von Condorcet, Legendre und dann Jacobi sieht man es in alter französischer Schreibschrift, oder als eine Variante des kursiven kyrillischen d) wird ein partielles Differential bezeichnet.
• Mit $\delta$ (dem griechischen kleinen Delta) wird eine virtuelle Verschiebung, die Variation eines Ortsvektors bezeichnet. Sie hängt also mit dem partiellen Differential nach den einzelnen Raumdimensionen des Ortsvektors zusammen.
• Mit $\delta$ wird ein inexaktes Differential bezeichnet.

Totales Differential

Vorlage:Hauptartikel Das totale Differential oder vollständige Differential einer differenzierbaren Funktion $f(x_1,\dots ,x_n)$ in $n$ Variablen ist definiert durch

$\mathrm{d}f=\sum _{i=1}^n\frac{\partial f}{\partial x_i}\mathrm{d}{x}_i$.

Dies ist wieder interpretierbar als der lineare Anteil des Zuwachses. Eine Änderung des Arguments um $\mathrm{\Delta }x$ bewirkt eine Änderung des Funktionswertes um $\mathrm{\Delta }y=f(x+\mathrm{\Delta }x)-f(x)$, welche zerlegbar ist als

$\mathrm{\Delta }y=\mathrm{grad}f(x)\cdot \mathrm{\Delta }x+r(\mathrm{\Delta }x)$,

wobei der erste Summand das Skalarprodukt der beiden $n$-elementigen Vektoren $\mathrm{grad}f(x)=(\frac{\partial f}{\partial x_1}(x),\dots ,\frac{\partial f}{\partial x_n}(x))$ und $\mathrm{\Delta }x$ darstellt und der Rest von höherer Ordnung verschwindet, also $\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{r(\mathrm{\Delta }x)}{\parallel \mathrm{\Delta }x\parallel }=0$.

Virtuelle Verschiebung

Vorlage:Hauptartikel Eine virtuelle Verschiebung $\delta {𝐱}_i$ ist eine fiktive infinitesimale Verschiebung des $i$-ten Teilchens, die mit Zwangsbedingungen verträglich ist. Die Abhängigkeit von der Zeit wird nicht betrachtet. Aus dem totalen Differential $\mathrm{d}g=\sum _{i=1}^n\frac{\partial g}{\partial q_i}\mathrm{d}{q}_i+\frac{\partial g}{\partial t}\mathrm{d}t$  einer Funktion $g(q_1,\dots ,q_n,t)$ entsteht die gesuchte virtuelle Änderung $\delta g=\sum _{i=1}^n\frac{\partial g}{\partial q_i}\delta q_i$. Der Begriff „instantan“ ist dadurch mathematisiert.

Die $s$ holonomen Zwangsbedingungen, $f_l({𝐱}_1,\dots ,{𝐱}_N,t)=0,l=1,\dots ,s$  ,  werden durch Verwendung von $n=3N-s$ sogenannter generalisierter Koordinaten $q_k$ erfüllt:

$\delta {𝐱}_i=\sum _{k=1}^n\frac{\partial {𝐱}_i}{\partial q_k}\delta q_k$

Die holonomen Zwangsbedingungen werden also durch Auswahl und entsprechende Reduzierung der generalisierten Koordinaten explizit eliminiert.

Stochastische Analysis

In der stochastischen Analysis wird die Differentialschreibweise häufig angewendet, etwa zur Notation stochastischer Differentialgleichungen; sie ist dann stets als Kurzschreibweise für eine entsprechende Gleichung von Itō-Integralen aufzufassen. Ist beispielsweise $(H_t{)}_{t\ge 0}$ ein stochastischer Prozess, der bezüglich eines Wiener-Prozesses $(W_t{)}_{t\ge 0}$ Itō-integrierbar ist, dann wird die durch

$X_t=X_0+\underset{0}{\overset{t}{\int }}{H}_s\mathrm{d}{W}_s,t\ge 0$

gegebene Gleichung für einen Prozess $(X_t{)}_{t\ge 0}$ in Differentialform als $\mathrm{d}{X}_t=H_t\mathrm{d}{W}_t$ notiert. Die oben genannten Rechenregeln für Differentiale sind jedoch im Fall stochastischer Prozesse mit nichtverschwindender quadratischer Variation gemäß der Itō-Formel zu modifizieren.

Heutiger Zugang: Differentiale als 1-Formen

Vorlage:Hauptartikel Die oben gegebene Definition des Differentials $df$ entspricht in heutiger Terminologie dem Begriff der exakten 1-Form $df$.

Es sei $U$ eine offene Teilmenge des ${ℝ}^n$. Eine 1-Form oder Pfaffsche Form $\omega$ auf $U$ ordnet jedem Punkt $p\in U$ eine Linearform ${\omega }_p:{\mathrm{T}}_{p}U\to ℝ$ zu. Derartige Linearformen heißen Kotangentialvektoren; sie sind Elemente des Dualraumes ${\mathrm{T}}_p^{*}U$ des Tangentialraumes ${\mathrm{T}}_{p}U$. Eine pfaffsche Form $\omega$ ist also eine Abbildung

$\omega :U\to \underset{p\in U}{⨆}{\mathrm{T}}_p^{*}U,p\mapsto {\omega }_p\in {\mathrm{T}}_p^{*}U.$

Das totale Differential oder die äußere Ableitung $\mathrm{d}f$ einer differenzierbaren Funktion $f:U\to ℝ$ ist die pfaffsche Form, die folgendermaßen definiert ist: Ist $X\in {\mathrm{T}}_{p}U$ ein Tangentialvektor, so ist: $(\mathrm{d}f{)}_p(X)=Xf,$ also gleich der Richtungsableitung von $f$ in Richtung $X$. Ist also $\gamma :(-\epsilon ,\epsilon )\to U$ ein Weg mit $\gamma (0)=p$ und $\dot{\gamma }(0)=X$, so ist

$(\mathrm{d}f{)}_p(X)={\frac{\mathrm{d}}{\mathrm{d}t}|}_{t=0}f(\gamma (t)).$

Mit Hilfe des Gradienten und des Standard-Skalarproduktes lässt sich das totale Differential von $f$ durch

$(\mathrm{d}f{)}_p(X)=⟨\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}f,X⟩$

darstellen.

Für $n=1$ erhält man insbesondere das Differential $df$ von Funktionen $f:ℝ\to ℝ$.

Differentiale in der Integralrechnung

Anschauliche Erklärung

Um den Flächeninhalt eines Bereiches zu berechnen, der von dem Graphen einer Funktion $f$, der $x$-Achse und zwei dazu senkrechten Geraden $x=a$ und $x=b$ eingeschlossen wird, unterteilte man die Fläche in Rechtecke der Breite $\mathrm{\Delta }x$, die „unendlich schmal“ gemacht werden, und der Höhe $f(x)$. Ihr jeweiliger Flächeninhalt ist das „Produkt“

$f(x)\cdot \mathrm{\Delta }x$,

der gesamte Flächeninhalt also die Summe

$\underset{a}{\overset{b}{\int }}f(x)\cdot \mathrm{d}x$

wobei hier $\mathrm{d}x$ wieder eine endliche Größe ist, die einer Unterteilung des Intervalls $[a,b]$ entspricht. Siehe genauer: Mittelwertsatz der Integralrechnung. Es gibt im Intervall $[a,b]$ einen festen Wert $\xi$, dessen Funktionswert multipliziert mit der Summe der endlichen $\mathrm{d}x$ des Intervalls $[a,b]$ den Wert des Integrals dieser einen stetigen Funktion wiedergibt:

$\underset{a}{\overset{b}{\int }}f(x)\cdot \mathrm{d}x=f(\xi )\cdot \underset{a}{\overset{b}{\int }}\mathrm{d}x$

Das Gesamtintervall $[a,b]$ des Integrals muss nicht gleichmäßig unterteilt sein. Die Differentiale an den unterschiedlichen Unterteilungsstellen können verschieden groß gewählt sein, die Wahl der Unterteilung des Integrationsintervalls hängt oft von der Art des Integrationsproblems ab. Zusammen mit dem Funktionswert innerhalb des „differentiellen“ Intervalls (beziehungsweise des Maximal- und Minimalwerts darinnen entsprechend Ober- und Untersumme) bildet sich eine Flächengröße; man macht den Grenzwertübergang in dem Sinne, dass man die Unterteilung von $[a,b]$ immer feiner wählt. Das Integral ist eine Definition für eine Fläche mit Begrenzung durch ein Kurvenstück.

Formale Erklärung

Vorlage:Hauptartikel Es sei $f:ℝ\to ℝ$ eine integrierbare Funktion mit Stammfunktion $F:ℝ\to ℝ$. Das Differential

$\mathrm{d}F=f(x)\mathrm{d}x$

ist eine 1-Form, die nach den Regeln der Integration von Differentialformen integriert werden kann. Das Ergebnis der Integration über ein Intervall $[a,b]$ ist genau das Lebesgue-Integral

$\underset{a}{\overset{b}{\int }}f(x)\mathrm{d}x$.

Spezielle Differentiale

Im Zusammenhang mit den folgenden Integralen hat das jeweilige Differential eine besondere Bezeichnung und auch Bedeutung:

• Linienelement beim Kurvenintegral
• Oberflächenelement (skalar und vektoriell) beim Oberflächenintegral
• Volumenelement beim Volumenintegral.

Die Differentiale hängen dabei vom verwendeten Koordinatensystem ab.

Differentiale als Rechenhilfe

Indem man mit einem Differential wie mit einer Variablen rechnet – was streng genommen nicht zulässig ist – vereinfachen sich manche Rechnungen. Dieses Vorgehen wird insbesondere in der Physik angewendet. Aber auch in der Mathematik liefert diese Methode oft die Vorlage für exakte Beweise – zum Beispiel beim Beweis der Kettenregel.

Beispiel 1 (Integration durch Substitution)

Vorlage:Hauptartikel Das Integral

$\int x\sin (x^2+1)\mathrm{d}x$

soll berechnet werden. Die Substitution $t=x^2+1$ ergibt die Ableitung $\frac{\mathrm{d}t}{\mathrm{d}x}=2x$ und somit für die Differentiale $\mathrm{d}t=2x\mathrm{d}x$. Damit erhält man

$\int x\sin (x^2+1)\mathrm{d}x=\frac{1}{2}\int 2x\sin (x^2+1)\mathrm{d}x=\frac{1}{2}\int \sin (t)\mathrm{d}t=-\frac{1}{2}\cos (t)+C=-\frac{1}{2}\cos (x^2+1)+C,$ mit $C\in ℝ$.

Beispiel 2 (Separation der Variablen)

Vorlage:Hauptartikel Die Differentialgleichung

$f^{\prime }(x)=-k\cdot f(x)$

mit der Anfangsbedingung $f(0)=C_0(C_0\in ℝ)$ soll gelöst werden. Setzt man $y=f(x)$ und $\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}x}=f^{\prime }(x)$, so erhält man

$\frac{\mathrm{d}y}{\mathrm{d}x}=-k\cdot y$.

Multipliziert man nun beide Seiten mit dem Differential $\mathrm{d}x$ und trennt die Variablen, indem man sie auf jeweils eine Seite der Gleichung bringt, so ergibt sich

$\frac{1}{y}\mathrm{d}y=-k\mathrm{d}x$.

Integration und Berücksichtigung der Anfangsbedingung ergeben die Lösung:

$\int \frac{1}{y}\mathrm{d}y=-k\int \mathrm{d}x$

$ln(y)=-k\cdot x+C,(C\in ℝ)$

$ln(f(x))=-k\cdot x+C$

$f(x)=C_0\cdot \exp (-k\cdot x)$.

Beispiel 3 (Kurvenintegral)

Vorlage:Hauptartikel Es soll der Umfang eines Kreises mit Radius $r$ berechnet werden. Der Ortsvektor $\overrightarrow{r}$ zu einem Punkt einer kreisförmigen Kurve lautet

$\overrightarrow{r}=\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}r\cos t\\ r\sin t\end{array}\right)$ mit $t\in [0,2\pi ]$.

Durch Ableitung nach der Variablen t ergibt sich sein Differential

$d\overrightarrow{r}=\left(\begin{array}{c}dx\\ dy\end{array}\right)=\left(\begin{array}{c}-r\sin t\\ r\cos t\end{array}\right)dt$,

das als infinitesimaler Tangentenvektor gedeutet werden kann. Für seine Länge $ds$ gilt:

$ds=\sqrt{d\overrightarrow{r}d\overrightarrow{r}}=\sqrt{r^2{\sin }^{2}t+r^2{\cos }^{2}t}dt=rdt$.

Damit ergibt sich der Umfang $U$ des Kreises durch das Kurvenintegral

$U=\underset{0}{\overset{2\pi }{\int }}rdt=2r\pi$.

Beispiel 4 (Volumen eines Kegels)

Vorlage:Hauptartikel Ein auf der Spitze stehender gerader oder schiefer Kegel mit Radius $r$ und Höhe $h$ wird von einer Ebene parallel zur Grundfläche im Abstand $x$ von der Spitze geschnitten. Mit dem Radius $r_s$ des Schnittkreises ergibt sich nach dem Strahlensatz:

$\frac{r_s}{x}=\frac{r}{h}$.

Das Volumen eines infinitesimalen Zylinders mit dem Schnittkreis als Grundfläche ist

$dV={r_s}^2\pi dx=\frac{r^2}{h^2}{x}^2\pi dx$.

Durch Integration erhält man das Volumen $V$des Kegels:

$V=\underset{0}{\overset{h}{\int }}\frac{r^2}{h^2}{x}^2\pi dx=\frac{1}{3}{r}^2\pi h$.

Historisches

Gottfried Wilhelm Leibniz verwendet erstmals in einem Manuskript 1675 in der Abhandlung Analysis tetragonistica das Integralzeichen, er schreibt nicht $\int f(x)\mathrm{d}x$ sondern $\int f(x)$. Am 11. November 1675 verfasste Leibniz einen Aufsatz mit dem Titel „Beispiele zur umgekehrten Tangentenmethode“ und hier kommt neben $\int f(x)$ zum ersten Mal $\int f(x)\mathrm{d}x$ vor, ebenso statt $\frac{x}{d}$ die Schreibweise $\mathrm{d}x$.

In der modernen Fassung dieses Zugangs zur Integralrechnung nach Bernhard Riemann ist das „Integral“ ein Grenzwert der Flächeninhalte endlich vieler Rechtecke endlicher Breite für immer feinere Unterteilungen des „$x$-Bereichs“.

Deshalb ist das erste Symbol im Integral ein stilisiertes S für „Summe“. „Utile erit scribi $\int$ pro omnia (Es wird nützlich sein, $\int$ anstatt omnia zu schreiben) und ∫ l um die Summe einer Gesamtheit ∫ zu bezeichnen … Hier zeigt sich eine neue Gattung des Kalküls; ist dagegen $\int l=ya$ gegeben, so bietet sich ein entgegengesetzter Kalkül mit der Bezeichnung $l=\frac{ya}{d}$, wie nämlich ∫ die Abmessungen vermehrt, so vermindert sie d. ∫ bedeutet aber die Summe, d die Differenz.“ schreibt Leibniz am 29. Oktober 1675 in einer Untersuchung, in der er die Cavalierischen Gesamtheiten verwendet. In der späteren Niederschrift von 11. November 1675 geht er von der Schreibweise $\frac{x}{d}$ zu $dx$ über, er verzeichnet in einer Fußnote „$dx$ ist gleich $\frac{x}{d}$“, in derselben Rechnung kommt auch die Formel $\int y\mathrm{d}y=\frac{y^2}{2}$ vor. Omnia steht dabei für omnia l und wird in dem geometrisch orientierten Flächenberechnungsverfahren von Bonaventura Cavalieri verwendet. Die zugehörige gedruckte Veröffentlichung Leibniz’ ist De geometria recondita aus dem Jahr 1686. Leibniz gab sich mit der Bezeichnungsweise Mühe, „um die Rechnung kalkülmäßig einfach und zwangsläufig zu machen.“

Blaise Pascals Betrachtungen zum Viertelkreisbogen: Quarts de Cercle

Das charakteristische Dreieck

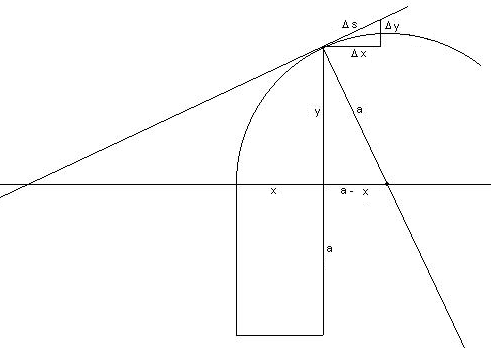
Als Leibniz als junger Mann 1673 in Paris war, empfing er eine entscheidende Anregung durch eine Betrachtung Pascals in dessen 1659 erschienener Schrift Traité des sinus des quarts de cercle (Abhandlung über den Sinus des Viertelkreises). Er sagt, er habe darin ein Licht gesehen, das der Autor nicht bemerkt habe. Es handelt sich um folgendes (in moderner Terminologie geschrieben, siehe Abbildung):

Um das statische Moment

$\underset{0}{\overset{\frac{1}{2}a\pi }{\int }}y\mathrm{d}s$

des Viertelkreisbogens bezüglich der x-Achse zu bestimmen, schließt Pascal aus der Ähnlichkeit der Dreiecke mit den Seiten

$(\mathrm{\Delta }x,\mathrm{\Delta }y,\mathrm{\Delta }s)$

und

$(y,(a-x),a),$

dass ihr Seitenverhältnis gleich ist

$\frac{\mathrm{\Delta }s}{a}=\frac{\mathrm{\Delta }x}{y},$

und somit

$y\cdot \mathrm{\Delta }s=a\cdot \mathrm{\Delta }x,$

so dass

$\underset{0}{\overset{\frac{1}{2}a\pi }{\int }}y\mathrm{d}s=\underset{0}{\overset{a}{\int }}a\mathrm{d}x=a^2$

gilt. Leibniz bemerkte nun – und dies war das „Licht“, das er sah –, dass dieses Verfahren nicht auf den Kreis beschränkt ist, sondern allgemein für jede (glatte) Kurve gilt, sofern der Kreisradius a durch die Länge der Kurvennormalen (die reziproke Krümmung, der Radius des Krümmungskreises) ersetzt wird. Das infinitesimale Dreieck

$(\mathrm{\Delta }x,\mathrm{\Delta }y,\mathrm{\Delta }s)$

ist das charakteristische Dreieck (Es findet sich auch bei Isaac Barrow zur Tangentenbestimmung.) Es ist bemerkenswert, dass die spätere Leibniz’sche Symbolik der Differentialrechnung (dx, dy, ds) gerade dem Standpunkt dieser „verbesserten Indivisibilienvorstellung“ entspricht.

Ähnlichkeit

Alle Dreiecke aus einem Abschnitt $\mathrm{\Delta }s$ der Tangente zusammen mit den zur jeweiligen x- und y-Achse parallelen Stücken $\mathrm{\Delta }x$ und $\mathrm{\Delta }y$ bilden mit dem Dreieck aus Krümmungskreisradius a, Subnormaler $x-a$ und Ordinate y ähnliche Dreiecke und behalten deren Verhältnisse entsprechend der Steigung der Tangente an den Krümmungskreis in diesem Punkt auch bei, wenn der Grenzwertübergang gemacht wird. Das Verhältnis von $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$ ist ja genau die Steigung von $\mathrm{\Delta }s$. Deshalb kann man für jeden Krümmungskreis an einem Punkt der Kurve dessen (charakteristische) Proportionen im Koordinatensystem auf die Differentiale dort übertragen, insbesondere wenn sie als infinitesimale Größen aufgefasst werden.

Nova methodus 1684

Tafel XII

Erste inhaltliche Seite

Neue Methode der Maxima, Minima sowie der Tangenten, die sich weder an gebrochenen, noch an irrationalen Größen stößt, und eine eigentümliche darauf bezügliche Rechnungsart. (Leibniz (G. G. L.), Acta eruditorum 1684)

Leibniz erläutert hier sehr kurz auf vier Seiten seine Methode. Er wählt ein beliebiges unabhängiges festes Differential (hier dx, s. Abb. r. o.) und gibt die Rechenregeln, wie unten, für die Differentiale an, beschreibt, wie man sie bildet.

Danach gibt er die Kettenregel an: Vorlage:Zitat

Das ist aus heutiger Sicht ungewohnt, weil er unabhängige und abhängige Differentiale gleich und einzeln, und nicht wie abschließend benötigt, den Differentialquotienten aus abhängiger und unabhängiger Größe betrachtet. Andersherum, wenn er eine Lösung angibt, ist die Bildung des Differentialquotienten möglich. Er behandelt die gesamte Bandbreite der rationalen Funktionen. Es folgen ein formales kompliziertes Beispiel, ein dioptrisches der Lichtbrechung (Minimum), ein leicht lösbares geometrisches, mit verwickelten Abstandsverhältnissen, und eines, das den Logarithmus behandelt.

Weitere Zusammenhänge werden wissenschaftlich historisch bei ihm aus dem Zusammenhang mit früheren und späteren Arbeiten zu dem Thema betrachtet, die teils nur handschriftlich oder in Briefen und nicht veröffentlicht vorliegen. In Nova methodus 1684 steht zum Beispiel nicht, dass für das unabhängige dx gilt dx = const. und ddx=0. In weiteren Beiträgen behandelt er das Thema bis zu „Wurzeln“ und Quadraturen von unendlichen Reihen.

Grafische Veranschaulichung des Beauneschen Problems

Das Verhältnis von Unendlichklein und bekanntes Differential (= Größe) beschreibt Leibniz: Vorlage:Zitat Für die transzendente Linie wird die Zykloide als Nachweis herangezogen.

Als Anhang erklärt er 1684 die Lösung eines Problems, das Florimond de Beaune Descartes stellte, und das er nicht löste. Das Problem sieht vor, dass eine Funktion (w, der Linie WW in Tafel XII) gefunden wird, deren Tangente (WC) die x-Achse immer so schneidet, dass der Abschnitt zwischen Schnittpunkt der Tangente mit der x Achse und dessen Abstand zur zugehörigen Abszisse x, dort wählt er dx immer gleich b, konstant, er nennt es hier a, ist. Diese Proportionalität vergleicht er mit der arithmetischen Reihe und der geometrischen und erhält als Abszisse die Logarithmen und als Ordinate die Numeri. „Es werden also die Ordinaten w“ (Wertzunahme) „den dw“ (Steigungszunahme)", ihren Inkrementen oder Differenzen, proportional, …" Er gibt die Logarithmusfunktion als Lösung an: „… wenn die w die Numeri sind, so sind die x die Logarithmen.“: w=a/b dw, oder w dx = a dw. Dies erfüllt

$\log w=\frac{x}{a}+\log c$

oder

$w=c{e}^{\frac{x}{a}}.$

Cauchys Differentialbegriff

In den 1980er Jahren fand in Deutschland eine Auseinandersetzung statt, inwieweit die Grundlegung der Analysis bei Cauchy logisch einwandfrei ist. Detlef Laugwitz versucht mit Hilfe einer historischen Lesart Cauchys, den Begriff unendlich kleiner Größen für seine $\mathrm{\Omega }$-Zahlen fruchtbar zu machen, findet aber daraus resultierend bei Cauchy Unstimmigkeiten. Detlef Spalt korrigiert den (ersten!) historischen Lesansatz der cauchyschen Arbeiten und fordert die Verwendung von Begriffen aus Cauchys Zeit und nicht heutigen Begriffen zum Nachweis seiner Sätze und kommt zu dem Ergebnis, dass Cauchys Grundlegung der Analysis logisch einwandfrei ist, jedoch bleiben weiterhin die Fragen nach der Behandlung unendlich kleiner Größen offen.

Die Differentiale bei Cauchy sind endlich und konstant $\mathrm{d}x=h$ ($h$ endlich). Der Wert der Konstanten ist nicht näher bestimmt.

$\mathrm{\Delta }x$ ist bei Cauchy unendlich klein und veränderlich.

Die Beziehung zu $h$ ist $\mathrm{\Delta }x=i=\alpha h$, wobei $h$ endlich und $\alpha$ infinitesimal (unendlich klein) ist.

Ihr geometrisches Verhältnis ist als

$\frac{\mathrm{d}y}{\mathrm{d}x}=\underset{\alpha =0}{\lim }\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$

bestimmt. Dieses Verhältnis unendlich kleiner Größen, oder genauer die Grenze geometrischer Differenzenverhältnisse abhängiger Zahlgrößen, einen Quotienten, kann Cauchy auf endliche Größen übertragen.

Differentiale sind endliche Zahlgrößen, deren geometrische Verhältnisse streng gleich den Grenzen der geometrischen Verhältnisse sind, welche aus den unendlich kleinen Zuwächsen der vorgelegten unabhängigen Veränderlichen oder der Veränderlichen der Funktionen gebildet sind. Cauchy hält es für wichtig Differentiale als endliche Zahlgrößen zu betrachten.

Der Rechner bedient sich der Unendlichkleinen als Vermittelnden, welche ihn zu der Kenntnis der Beziehung führen müssen, die zwischen den endlichen Zahlgrößen bestehen; und nach Cauchys Meinung dürfen die Unendlich kleinen in den Schlussgleichungen, wo ihre Anwesenheit sinnlos, zwecklos und nutzlos bliebe, nie zugelassen werden. Außerdem: Wenn man die Differentiale als beständig sehr kleine Zahlgrößen betrachtete, dann gäbe man dadurch den Vorteil auf, der darin besteht, dass man unter den Differentialen von mehreren Veränderlichen das eine als Einheit nehmen kann. Denn um eine klare Vorstellung einer beliebigen Zahlgröße auszubilden, ist es wichtig, sie auf die Einheit ihrer Gattung zu beziehen. Es ist also wichtig, unter den Differentialen eine Einheit auszuwählen.

Insbesondere fällt für Cauchy die Schwierigkeit weg, höhere Differentiale zu definieren. Denn Cauchy setzt $\mathrm{d}x=h$ nachdem er die Rechenregeln der Differentiale durch Übergang zu den Grenzen erhalten hat. Und da das Differential einer Funktion der Veränderlichen $x$ eine andere Funktion dieser Veränderlichen ist, kann er $y$ mehrmals differenzieren und erhält in dieser Weise die Differentiale verschiedener Ordnungen.

$\mathrm{d}y=\mathrm{d}y=h\cdot y^{\prime }=y^{\prime }\mathrm{d}x$

$\mathrm{d}\mathrm{d}y={\mathrm{d}}^{2}y=h\mathrm{d}{y}^{\prime }=y^{″}{h}^2$

$\mathrm{d}\mathrm{d}\mathrm{d}y={\mathrm{d}}^{3}y=h^2\mathrm{d}{y}^{″}=y^{‴}{h}^3$

…

Literatur

• Gottfried Leibniz, Sir Isaac Newton: Über die Analysis des Unendlichen – Abhandlung über die Quadratur der Kurven. Verlag Harri Deutsch, ISBN 3-8171-3162-3 (Ostwalds Klassiker der exakten Wissenschaften, Band 162).
• Oskar Becker: Grundlagen der Mathematik. Suhrkamp Verlag, ISBN 3-518-07714-7.
• Detlef Spalt: Die Vernunft im Cauchy-Mythos. Verlag Harri Deutsch, ISBN 3-8171-1480-X (Spalt problematisiert die Übernahme moderner Begriffe auf frühere Analysis, stellt fest, dass Cauchys Aufbau der Analysis logisch einwandfrei ist, thematisiert benachbarte Begriffe und lässt Cauchy virtuelle Diskussionen mit wesentlich jüngeren Mathematikern führen über deren begriffliche Genauigkeit, z. B. Abel etc.)
• K. Popp, E. Stein (Hrsg.): Gottfried Wilhelm Leibniz, Philosoph, Mathematiker, Physiker, Techniker. Schlütersche, Hannover 2000, ISBN 3-87706-609-7.
• Henk Bos: Differentials, Higher-Order Differentials and the Derivative in the Leibnizian Calculus. In: Archive for History of Exact Sciences, 14, 1974, S. 1–90. Heftig diskutierte Veröffentlichung aus den 1970ern, um Kontinuum und Unendlichkeit.
• Courant: Vorlesungen über Differential- und Integralrechnung. Springer, 1971
• Joos, Kaluza: Höhere Mathematik für den Praktiker. in älteren Auflagen so z. B. 1942, Johann Ambriosius Barth.
• Duden Rechnen und Mathematik. Dudenverlag, 1989.
• Vorlage:Literatur
• Vorlage:Literatur