Fibonacci-Folge

Kachelmuster aus Quadraten, deren Kantenlängen der Fibonacci-Folge entsprechen

Angenäherte Goldene Spirale, konstruiert mit Viertelkreisen. Das Verhältnis der aufeinander folgenden Radien ist das der aufeinander folgenden Fibonacci-Zahlen (Φ bei der Goldenen Spirale).

In Anlehnung an den Pythagoras-Baum lassen sich die Fibonacci-Zahlen auch spiralförmig als Flächenmaßzahlen von Katheten- und Hypotenusenquadraten darstellen.

Die Fibonacci-Folge ist die unendliche Folge natürlicher Zahlen, die mit zweimal der Zahl 1 beginnt und bei der jede weitere Zahl die Summe der beiden ihr vorangehenden Zahlen ist. In moderner Schreibweise wird diese Folge zusätzlich mit einer führenden Zahl 0 versehen:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …

Die darin enthaltenen Zahlen heißen Fibonacci-Zahlen. Benannt ist die Folge nach Leonardo Fibonacci, der damit im Jahr 1202 das Wachstum einer Kaninchenpopulation beschrieb. Die Folge war aber schon in der Antike sowohl den Griechen als auch den Indern bekannt.

Weitere Untersuchungen zeigten, dass die Fibonacci-Folge auch noch zahlreiche andere Wachstumsvorgänge in der Natur beschreibt. Es scheint, als sei sie eine Art Wachstumsmuster in der Natur.

Die Fibonacci-Zahlen weisen einige bemerkenswerte mathematische Besonderheiten auf:

• Aufgrund der Beziehung zur vorherigen und zur folgenden Zahl scheint Wachstum in der Natur einem Additionsgesetz zu folgen.
• Je weiter man in der Folge fortschreitet, desto mehr nähert sich der Quotient aufeinanderfolgender Fibonacci-Zahlen dem Teilungsverhältnis des Goldenen Schnittes $\mathrm{\Phi }=1,6180\dots$ (beispielsweise 13:8 = 1,6250; 21:13 ≈ 1,6154; 34:21 ≈ 1,6190; 55:34 ≈ 1,6176; etc.). Diese Näherung ist alternierend, d. h., die Quotienten sind abwechselnd kleiner und größer als $\mathrm{\Phi }$.

Definition der Fibonacci-Folge

Die ersten Folgenglieder der Fibonacci-Folge

Die Fibonacci-Folge $f_1,f_2,f_3,\dots$ ist durch das rekursive Bildungsgesetz

$f_n=f_{n-1}+f_{n-2}$   für   $n\ge 3$

mit den Anfangswerten

$f_1=f_2=1$

definiert. Das bedeutet in Worten:

• Für die beiden ersten Zahlen wird der Wert $1$ vorgegeben.
• Jede weitere Zahl ist die Summe ihrer beiden Vorgänger in der Folge.

Daraus ergibt sich:

n	fn		n	fn		n	fn		n	fn		n	fn
1	1		11	89		21	10 946		31	1 346 269		41	165 580 141
2	1		12	144		22	17 711		32	2 178 309		42	267 914 296
3	2		13	233		23	28 657		33	3 524 578		43	433 494 437
4	3		14	377		24	46 368		34	5 702 887		44	701 408 733
5	5		15	610		25	75 025		35	9 227 465		45	1 134 903 170
6	8		16	987		26	121 393		36	14 930 352		46	1 836 311 903
7	13		17	1 597		27	196 418		37	24 157 817		47	2 971 215 073
8	21		18	2 584		28	317 811		38	39 088 169		48	4 807 526 976
9	34		19	4 181		29	514 229		39	63 245 986		49	7 778 742 049
10	55		20	6 765		30	832 040		40	102 334 155		50	12 586 269 025

Aus der Forderung, dass die Rekursion

$f_n=f_{n-1}+f_{n-2}$

auch für ganze Zahlen $n\le 2$ gelten soll, erhält man eine eindeutige Fortsetzung auf den Index 0 und auf negative Indizes. Es gilt:

$f_0=0$

$f_{-n}=(-1{)}^{n+1}{f}_n$ für alle $n>0$

Vorlage:AnkerDie so erweiterte Fibonacci-Folge lautet dann

$f_{-7}$

$f_{-6}$

$f_{-5}$

$f_{-4}$

$f_{-3}$

$f_{-2}$

$f_{-1}$

$f_0$

$f_1$

$f_2$

$f_3$

$f_4$

$f_5$

$f_6$

$f_7$

$\cdots$

13

−8

5

−3

2

−1

1

0

1

1

2

3

5

8

13

$\cdots$

und heißt Folge der negaFibonacci-Zahlen.

Darüber hinaus ist eine Verallgemeinerung der Fibonacci-Zahlen auf komplexe Zahlen, proendliche Zahlen und auf Vektorräume möglich.

Eigenschaften

Zu den zahlreichen bemerkenswerten Eigenschaften der Fibonacci-Zahlen gehört, dass sie dem Benfordschen Gesetz genügen.

Näherung an den Goldenen Schnitt

Wie von Johannes Kepler festgestellt wurde, kommen die Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen dem Goldenen Schnitt

$\mathrm{\Phi }:=\frac{1+\sqrt{5}}{2}\approx 1,6180$

beliebig nahe. Dies folgt unmittelbar aus der Näherungsformel für große Zahlen $n$:

$\underset{n\to \mathrm{\infty }}{\lim }\frac{f_{n+1}}{f_n}=\underset{n\to \mathrm{\infty }}{\lim }\frac{{\mathrm{\Phi }}^{n+1}}{{\mathrm{\Phi }}^n}=\mathrm{\Phi }$

Diese Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen haben eine bemerkenswerte Kettenbruchdarstellung:

$\frac{1}{1}=1\frac{2}{1}=1+\frac{1}{1}=[1;1]\frac{3}{2}=1+\frac{1}{1+\frac{1}{1}}=[1;1,1]\frac{5}{3}=1+\frac{1}{1+\frac{1}{1+\frac{1}{1}}}=[1;1,1,1]$

mit der $[;]$-Notation aus dem Artikel Kettenbruch.

Da diese Quotienten gegen den Goldenen Schnitt konvergieren, lässt sich dieser als der unendliche periodische Kettenbruch darstellen:

$\mathrm{\Phi }=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{\ddots }}}}=[1;\bar{1}]$

Die Zahl $\mathrm{\Phi }$ ist irrational. Das bedeutet, dass sie sich nicht durch ein Verhältnis zweier ganzer Zahlen darstellen lässt. Am besten lässt sich $\mathrm{\Phi }$ durch Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen approximieren. Dies gilt auch für verallgemeinerte Fibonaccifolgen, bei denen $f_0$ und $f_1$ beliebige natürliche Zahlen annehmen.

Beziehungen zwischen den Folgengliedern

Identitäten:

• $f_{m+n}=f_{n+1}{f}_m+f_n{f}_{m-1}$
• $f_{m+n}=f_n{L}_m+(-1{)}^{m+1}{f}_{n-m}$ mit der Lucas-Folge $L_m=f_{m+1}+f_{m-1}={\mathrm{\Phi }}^m+{\mathrm{\Psi }}^m$ (mit $\mathrm{\Psi }:=1-\mathrm{\Phi }$), insbesondere:
• $f_{2n}=f_n{L}_n=f_n(f_{n+1}+f_{n-1})$
• $f_{2n+1}=f_n^2+f_{n+1}^2$
• $f_n^2-f_{n+k}{f}_{n-k}=(-1{)}^{n-k}{f}_k^2$ (Identität von Catalan)
• $f_{n+1}{f}_{n-1}-f_n^2=(-1{)}^n$ (Identität von Cassini, Spezialfall der Catalan-Identität)
• $f_m{f}_{n+1}-f_n{f}_{m+1}=(-1{)}^n{f}_{m-n}$ (Identität von d’Ocagne)

Teilbarkeit:

• $\mathrm{ggT}(f_m,f_n)=f_{\mathrm{ggT}(m,n)}$
• Je zwei benachbarte Fibonaccizahlen sind teilerfremd, d. h. $\mathrm{ggT}(f_n,f_{n+1})=1$.
• $m\mid n\Rightarrow f_m\mid f_n$; für $m>2$ gilt auch die Umkehrung. Insbesondere kann $f_n$ für $n>4$ nur dann eine Primzahl sein, wenn $n$ eine Primzahl ist.
• $2\mid f_n\iff 3\mid n$ (Genau jede dritte Fibonacci-Zahl ist durch 2 teilbar.)
• $3\mid f_n\iff 4\mid n$ (Genau jede vierte Fibonacci-Zahl ist durch 3 teilbar.)
• $4\mid f_n\iff 6\mid n$ (Genau jede sechste Fibonacci-Zahl ist durch 4 teilbar.)
• $5\mid f_n\iff 5\mid n$ (Genau jede fünfte Fibonacci-Zahl ist durch 5 teilbar.)
• $7\mid f_n\iff 8\mid n$ (Genau jede achte Fibonacci-Zahl ist durch 7 teilbar.)
• $16\mid f_n\iff 12\mid n$ (Genau jede zwölfte Fibonacci-Zahl ist durch 16 teilbar.)

Für die Teilbarkeit durch Primzahlen $p$ gilt unter Verwendung des Jacobi-Symbols:

• $p\mid f_{p-1}\iff \left(\frac{5}{p}\right)=1$
• $p\mid f_{p+1}\iff \left(\frac{5}{p}\right)=-1$

Summenformeln:

• $\sum _{i=0}^n{f}_i=f_{n+2}-1$
• $\sum _{i=1}^{2n}(-1{)}^{i-1}{f}_i=-f_{2n-1}+1$
• $\sum _{i=1}^{2n+1}(-1{)}^{i-1}{f}_i=f_{2n}+1$
• $\sum _{i=1}^n{f}_i^2=f_n{f}_{n+1}$
• $\sum _{i=1}^n{f}_{2i-1}=f_{2n}$
• $\sum _{i=1}^n{f}_{2i}=f_{2n+1}-1$
• $\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})f_i=f_{2n}$
• $\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n-i}{i})=f_{n+1}$

Es gibt noch zahlreiche weitere derartige Formeln.

Reziproke:

• Vorlage:Anker$\frac{1}{f_{2n}}=\sqrt{5}(\frac{{\mathrm{\Psi }}^{2n}}{1-{\mathrm{\Psi }}^{2n}}-\frac{{\mathrm{\Psi }}^{4n}}{1-{\mathrm{\Psi }}^{4n}})$

Zeckendorf-Theorem

Das nach Edouard Zeckendorf benannte Zeckendorf-Theorem besagt, dass jede natürliche Zahl $n>0$ eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender Fibonacci-Zahlen $f_i$ geschrieben werden kann. Das heißt, es gibt für jedes $n\in \mathbb{N},n>0$ eine eindeutige Darstellung der Form

$n=\sum _{i=2}^k{c}_i{f}_i$ mit $c_i\in \{0,1\}$ und $c_i{c}_{i+1}=0$ für alle $i$.

Die entstehende Folge ${\left(c_i\right)}_{i\in 2+{\mathbb{N}}_0}$ von Nullen und Einsen wird Zeckendorf-Sequenz genannt. Sehr eng hängt damit der Fibonacci-Kode zusammen.

Berechnung

Formel von Moivre-Binet

Das explizite Bildungsgesetz für die Glieder der Fibonacci-Folge wurde unabhängig voneinander von den französischen Mathematikern Abraham de Moivre im Jahr 1718 und Jacques Philippe Marie Binet im Jahr 1843 entdeckt. Dazwischen war es aber auch den Mathematikern Leonhard Euler und Daniel Bernoulli bekannt, Letzterer lieferte 1728 auch den vermutlich ersten Beweis.

Die Fibonacci-Zahlen lassen sich direkt mittels

$f_n=\frac{{\mathrm{\Phi }}^n-{\mathrm{\Psi }}^n}{\mathrm{\Phi }-\mathrm{\Psi }},n\in \mathbb{Z}$

berechnen, wobei $\mathrm{\Phi },\mathrm{\Psi }$ die beiden Lösungen der charakteristischen Gleichung $x^2-x-1=0$ sind. Mit

$\mathrm{\Phi }=\frac{1+\sqrt{5}}{2}$

$\mathrm{\Psi }=1-\mathrm{\Phi }=\frac{1-\sqrt{5}}{2}=-{\mathrm{\Phi }}^{-1}$

gilt explizit:

$f_n=\frac{{\mathrm{\Phi }}^n-{\mathrm{\Psi }}^n}{\sqrt{5}}=\frac{1}{\sqrt{5}}({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n)$

Bemerkenswert ist das Zusammenspiel zweier irrationaler Zahlen $\mathrm{\Phi }$ und $\mathrm{\Psi }$, das zu einem ganzzahligen Ergebnis führt.

Näherungsformel für große Zahlen

Der Einfluss von $\mathrm{\Psi }$ geht rasch gegen Null, bspw. ist $-\mathrm{\Psi }/\sqrt{5}\approx +0,276$. Das kann man verwenden, um die Berechnung abzukürzen, indem man die kleine Zahl $-{\mathrm{\Psi }}^n/\sqrt{5}$ einfach weglässt und das noch verbleibende ${\mathrm{\Phi }}^n/\sqrt{5}={\left(\frac{1+\sqrt{5}}{2}\right)}^n/\sqrt{5}$ kaufmännisch zur nächst gelegenen ganzen Zahl rundet. Mit Hilfe der Gaußschen Abrundungsfunktion $\lfloor \cdot \rfloor$ lässt sich das so formalisieren:

$f_n=\lfloor \frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^n+\frac{1}{2}\rfloor$ für alle $n\ge 0$

Induktiver Beweis

Einer der einfachsten Beweise gelingt induktiv. Wegen $\frac{{\mathrm{\Phi }}^0-{\mathrm{\Psi }}^0}{\sqrt{5}}=0=f_0$ und $\frac{{\mathrm{\Phi }}^1-{\mathrm{\Psi }}^1}{\sqrt{5}}=1=f_1$ ist der Induktionsanfang erfüllt. Angenommen, die Formel gelte für alle Werte von $0$ bis $n$ (starke Induktionsvoraussetzung). Wir zeigen, dass sie dann notwendigerweise auch für $n+1$ gilt:

$\begin{array}{cc}{f}_{n-1}+f_n& =\frac{{\mathrm{\Phi }}^{n-1}-{\mathrm{\Psi }}^{n-1}+{\mathrm{\Phi }}^n-{\mathrm{\Psi }}^n}{\sqrt{5}}\\ & =\frac{{\mathrm{\Phi }}^{n-1}(1+\mathrm{\Phi })-{\mathrm{\Psi }}^{n-1}(1+\mathrm{\Psi })}{\sqrt{5}}\\ & =\frac{{\mathrm{\Phi }}^{n-1}({\mathrm{\Phi }}^2)-{\mathrm{\Psi }}^{n-1}({\mathrm{\Psi }}^2)}{\sqrt{5}}\\ & =\frac{{\mathrm{\Phi }}^{n+1}-{\mathrm{\Psi }}^{n+1}}{\sqrt{5}}\\ & =f_{n+1}\end{array}$

Dabei haben wir benutzt, dass $\mathrm{\Phi }$ und $\mathrm{\Psi }$ der charakteristischen Gleichung $x^2=x+1$ genügen.

Nach dem Prinzip der vollständigen Induktion muss nun die Formel für alle $n$ gelten.

Herleitung über ein Eigenwertproblem

Die Formel von Binet kann mit Matrizenrechnung und dem Eigenwertproblem in der linearen Algebra hergeleitet werden mittels folgendem Ansatz:

${\left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right)}^n\left(\begin{array}{c}{f}_0\\ f_1\end{array}\right)=\left(\begin{array}{c}{f}_n\\ f_{n+1}\end{array}\right),f_0=0\text{ und }{f}_1=1\text{ mit }n\ge 0$

Nun transformiert man die Matrix $A=\left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right)$ in eine Diagonalmatrix $D$ durch Betrachtung als Eigenwertproblem.

Es gilt $A=TD{T}^{-1}$, wobei $T$ die Matrix der Eigenvektoren und $D$ die Diagonalmatrix mit den Eigenwerten ist. Damit folgt:

$\begin{array}{cc}{\left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right)}^n\left(\begin{array}{c}{f}_0\\ f_1\end{array}\right)& =A^n\left(\begin{array}{c}{f}_0\\ f_1\end{array}\right)={\left(TD{T}^{-1}\right)}^n\left(\begin{array}{c}{f}_0\\ f_1\end{array}\right)=T{D}^n{T}^{-1}\left(\begin{array}{c}0\\ 1\end{array}\right)\\ & =\left(\begin{array}{cc}\frac{-1-\sqrt{5}}{2}& \frac{-1+\sqrt{5}}{2}\\ 1& 1\end{array}\right){\left(\begin{array}{cc}\frac{1-\sqrt{5}}{2}& 0\\ 0& \frac{1+\sqrt{5}}{2}\end{array}\right)}^n\left(\begin{array}{cc}-\frac{1}{\sqrt{5}}& \frac{\sqrt{5}-1}{2\sqrt{5}}\\ \frac{1}{\sqrt{5}}& \frac{\sqrt{5}+1}{2\sqrt{5}}\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right)\\ & =\left(\begin{array}{cc}\frac{-1-\sqrt{5}}{2}& \frac{-1+\sqrt{5}}{2}\\ 1& 1\end{array}\right)\left(\begin{array}{cc}{\left(\frac{1-\sqrt{5}}{2}\right)}^n& 0\\ 0& {\left(\frac{1+\sqrt{5}}{2}\right)}^n\end{array}\right)\left(\begin{array}{cc}-\frac{1}{\sqrt{5}}& \frac{\sqrt{5}-1}{2\sqrt{5}}\\ \frac{1}{\sqrt{5}}& \frac{\sqrt{5}+1}{2\sqrt{5}}\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right)\\ & =\left(\begin{array}{cc}\frac{-1-\sqrt{5}}{2}{\left(\frac{1-\sqrt{5}}{2}\right)}^n& \frac{-1+\sqrt{5}}{2}{\left(\frac{1+\sqrt{5}}{2}\right)}^n\\ {\left(\frac{1-\sqrt{5}}{2}\right)}^n& {\left(\frac{1+\sqrt{5}}{2}\right)}^n\end{array}\right)\left(\begin{array}{c}\frac{\sqrt{5}-1}{2\sqrt{5}}\\ \frac{\sqrt{5}+1}{2\sqrt{5}}\end{array}\right)\\ & =\left(\begin{array}{c}-\frac{1}{\sqrt{5}}{\left(\frac{1-\sqrt{5}}{2}\right)}^n+\frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^n\\ -\frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right){\left(\frac{1-\sqrt{5}}{2}\right)}^n+\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^n\end{array}\right)\\ & =\left(\begin{array}{c}\frac{1}{\sqrt{5}}[{\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n]\\ \frac{1}{\sqrt{5}}[{\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}-{\left(\frac{1-\sqrt{5}}{2}\right)}^{n+1}]\end{array}\right)\\ & =\left(\begin{array}{c}{f}_n\\ f_{n+1}\end{array}\right)\end{array}$

Herleitung mittels Differenzengleichung

Eine andere Herleitungsmöglichkeit folgt aus der Theorie der linearen Differenzengleichungen:

Sei $C_n=x^n,n\in {\mathbb{N}}_0$ eine geometrische Folge, so ergibt sich:

$C_{n+1}-C_n-C_{n-1}=x^{n+1}-x^n-x^{n-1}=(x^2-x-1)x^{n-1}$

Wenn also $x$ so gewählt wird, dass die charakteristische Gleichung $x^2-x-1=0$ erfüllt ist (also $x=\mathrm{\Phi }$ oder $x=\mathrm{\Psi }$), wird $C_{n+1}=C_n+C_{n-1}$, d. h., $C_n$ erfüllt die Fibonacci-Rekursion mit dem Rekursionsanfang $C_0=1$ und $C_1=x$.

Die durch $A_0=1$, $A_1=\mathrm{\Phi }$, $A_{n+1}=A_n+A_{n-1}$ rekursiv definierte Folge hat die explizite Darstellung $A_n={\mathrm{\Phi }}^n$. Ebenso $B_0=1$, $B_1=\mathrm{\Psi }$, $B_n={\mathrm{\Psi }}^n$.

Mit $A_n$ und $B_n$ genügt wegen der Superpositionseigenschaft auch jede Linearkombination $L_n=\alpha A_n+\beta B_n$ der Fibonacci-Rekursion $L_{n+1}=L_n+L_{n-1}$. Mit Hilfe eines linearen Gleichungssystems ergibt sich $\alpha =\frac{1}{\sqrt{5}}$ und $\beta =-\frac{1}{\sqrt{5}}$, damit $L_0=\frac{{\mathrm{\Phi }}^0-{\mathrm{\Psi }}^0}{\sqrt{5}}=0=f_0$ und $L_1=\frac{{\mathrm{\Phi }}^1-{\mathrm{\Psi }}^1}{\sqrt{5}}=1=f_1$. Folglich ergibt sich explizit $F_n=\frac{A_n-B_n}{\sqrt{5}}=\frac{{\mathrm{\Phi }}^n-{\mathrm{\Psi }}^n}{\sqrt{5}}$.

Für $\alpha =\beta =1$ ergibt sich $L_0=2$ und $L_1=1$, d. h. die klassische Lucas-Folge mit explizit $L_n=A_n+B_n={\mathrm{\Phi }}^n+{\mathrm{\Psi }}^n$.

Herleitung mittels z-Transformation

Da Differenzengleichungen sehr elegant mittels z-Transformation beschrieben werden können, kann man die z-Transformation auch zur Herleitung der expliziten Formel für Fibonacci-Zahlen einsetzen. Im Artikel Einsatz der z-Transformation zur Bestimmung expliziter Formeln von Rekursionsvorschriften wird die allgemeine Vorgehensweise beschrieben und dann am Beispiel der Fibonacci-Zahlenfolge erläutert.

Alternierende Näherung

Die Quotienten aufeinanderfolgender Glieder der Fibonacci-Folge sind abwechselnd kleiner und größer als der Goldene Schnitt:

$\frac{f_{2n}}{f_{2n-1}}<\mathrm{\Phi }<\frac{f_{2n+1}}{f_{2n}}$

Herleitung

Mithilfe der Formel von Moivre-Binet lässt sich eine einfach Herleitung angeben. Denn für die Zahlen $\mathrm{\Phi },\mathrm{\Psi }$ der genannten Formel und natürliche $n>0$ gilt: $-\mathrm{\Phi }<0<-\mathrm{\Psi }|\cdot {\mathrm{\Psi }}^{2n}>0$ $-\mathrm{\Phi }{\mathrm{\Psi }}^{2n}<-{\mathrm{\Psi }}^{2n+1}|+{\mathrm{\Phi }}^{2n+1}$ ${\mathrm{\Phi }}^{2n+1}-\mathrm{\Phi }{\mathrm{\Psi }}^{2n}=\mathrm{\Phi }({\mathrm{\Phi }}^{2n}-{\mathrm{\Psi }}^{2n})<{\mathrm{\Phi }}^{2n+1}-{\mathrm{\Psi }}^{2n+1}|:({\mathrm{\Phi }}^{2n}-{\mathrm{\Psi }}^{2n})>0$(1) $\mathrm{\Phi }<\frac{{\mathrm{\Phi }}^{2n+1}-{\mathrm{\Psi }}^{2n+1}}{{\mathrm{\Phi }}^{2n}-{\mathrm{\Psi }}^{2n}}=\frac{f_{2n+1}}{f_{2n}}$, da im Doppelbruch der Darstellung der Folgeglieder mit Moivre-Binet der gemeinsame Nenner $\mathrm{\Phi }-\mathrm{\Psi }$ verschwindet. – Entsprechend: $-\mathrm{\Phi }<0<-\mathrm{\Psi }|\cdot {\mathrm{\Psi }}^{2n-1}<0$ $-\mathrm{\Phi }{\mathrm{\Psi }}^{2n-1}>-{\mathrm{\Psi }}^{2n}|+{\mathrm{\Phi }}^{2n}$ ${\mathrm{\Phi }}^{2n}-\mathrm{\Phi }{\mathrm{\Psi }}^{2n-1}=\mathrm{\Phi }({\mathrm{\Phi }}^{2n-1}-{\mathrm{\Psi }}^{2n-1})>{\mathrm{\Phi }}^{2n}-{\mathrm{\Psi }}^{2n}|:({\mathrm{\Phi }}^{2n-1}-{\mathrm{\Psi }}^{2n-1})>0$ $\mathrm{\Phi }>\frac{{\mathrm{\Phi }}^{2n}-{\mathrm{\Psi }}^{2n}}{{\mathrm{\Phi }}^{2n-1}-{\mathrm{\Psi }}^{2n-1}}=\frac{f_{2n}}{f_{2n-1}}$ (2) Die Ungleichungen (1) und (2) ergeben zusammen die Behauptung.

Die Differenz dieser oberen und unteren Schranke von $\mathrm{\Phi }$ konvergiert für wachsende $n$ rasch gegen Null wegen

$\frac{f_{2n+1}}{f_{2n}}-\frac{f_{2n}}{f_{2n-1}}=\frac{f_{2n+1}{f}_{2n-1}-f_{2n}^2}{f_{2n}{f}_{2n-1}}=\frac{1}{f_{2n}{f}_{2n-1}}.$

Bei der Vereinfachung des Zählers wurde die Identität von Cassini nebst $(-1{)}^{2n}=1$ verwendet.

Erzeugende Funktion

Eine erzeugende Funktion der Fibonacci-Zahlen ist

$\sum _{n=0}^{\mathrm{\infty }}{f}_n{z}^n=\frac{z}{1-z-z^2}=\frac{1}{\mathrm{\Phi }-\mathrm{\Psi }}(\frac{1}{1-\mathrm{\Phi }z}-\frac{1}{1-\mathrm{\Psi }z}).$

Die auf der linken Seite stehende Potenzreihe konvergiert für $|z|<1/\mathrm{\Phi }=0,618\dots$. Über die angegebene Partialbruchzerlegung erhält man wieder die Formel von Moivre-Binet.

Herleitung der erzeugenden Funktion

Für $G(z)=\sum _{n=0}^{\mathrm{\infty }}{f}_n{z}^n$ ist $\sum _{n=0}^{\mathrm{\infty }}{f}_{n+1}{z}^n=\sum _{n=1}^{\mathrm{\infty }}{f}_n{z}^{n-1}=z^{-1}\sum _{n=1}^{\mathrm{\infty }}{f}_n{z}^n=z^{-1}\sum _{n=0}^{\mathrm{\infty }}{f}_n{z}^n=\frac{G(z)}{z},$   da $f_0=0;$ $\sum _{n=0}^{\mathrm{\infty }}{f}_{n+2}{z}^n=\sum _{n=2}^{\mathrm{\infty }}{f}_n{z}^{n-2}=z^{-2}\sum _{n=2}^{\mathrm{\infty }}{f}_n{z}^n=z^{-2}(-z+\sum _{n=0}^{\mathrm{\infty }}{f}_n{z}^n)=\frac{G(z)-z}{z^2},$   da $f_0=0$ und $f_1=1.$ Die Rekursionsbedingung $f_{n+2}=f_{n+1}+f_n$ induziert daher $\sum _{n=0}^{\mathrm{\infty }}{f}_{n+2}{z}^n=\sum _{n=0}^{\mathrm{\infty }}{f}_{n+1}{z}^n+\sum _{n=0}^{\mathrm{\infty }}{f}_n{z}^n⟺$ $\frac{G(z)-z}{z^2}=\frac{G(z)}{z}+G(z)\mid \cdot z^2$ $G(z)-z=z\cdot G(z)+z^2\cdot G(z)\mid$ ausklammern: $G(z)\cdot (1-z-z^2)=z.$ Nach Division durch das Polynom $1-z-z^2,$ das nicht das Nullpolynom ist, folgt die angegebene Form.

Mit einer geeigneten erzeugenden Funktion lässt sich ein Zusammenhang zwischen den Fibonacci-Zahlen und den Binomialkoeffizienten darstellen:

$f_n=\sum _{k=0}^{[\frac{n-1}{2}]}(\genfrac{}{}{0ex}{}{n-k-1}{k})(n\ge 1)$

Wegen $(\genfrac{}{}{0ex}{}{n-k-1}{k})=0$ für $n-k-1\ge 0$ und $k>n-k-1$ kann auch ohne Gaußklammern geschrieben werden:

$f_n=\sum _{k=0}^{n-1}(\genfrac{}{}{0ex}{}{n-k-1}{k})=\sum _{k=1}^n(\genfrac{}{}{0ex}{}{n-k}{k-1})(n\ge 1)$

Herleitung

Die erzeugende Funktion kann auch geschrieben werden: $\sum _{n=0}^{\mathrm{\infty }}{f}_n{z}^n=0+\sum _{n=1}^{\mathrm{\infty }}{f}_n{z}^n=\frac{z}{1-z-z^2}$(1) für dem Betrage nach hinreichend kleine $z$ gilt: $\sum _{l=1}^{\mathrm{\infty }}(z+z^2{)}^l=\frac{z+z^2}{1-(z+z^2)}=\frac{z(1+z)}{1-z-z^2}\mid :(1+z)\ne 0$ $\sum _{l=1}^{\mathrm{\infty }}{z}^l(1+z{)}^{l-1}=\frac{z}{1-z-z^2}$(2) Gleichsetzen ergibt: $\sum _{n=1}^{\mathrm{\infty }}{f}_n{z}^n=\sum _{l=1}^{\mathrm{\infty }}{z}^l(1+z{)}^{l-1}=\sum _{l=1}^{\mathrm{\infty }}{z}^l\sum _{k=0}^{l-1}(\genfrac{}{}{0ex}{}{l-1}{k})z^k=\sum _{n=1}^{\mathrm{\infty }}{z}^n\sum _{k=0}^{[\frac{n-1}{2}]}(\genfrac{}{}{0ex}{}{n-k-1}{k})$, wobei [] Gaußklammern sind. Bei der Umformung wurden der binomische Lehrsatz und die Umsummierung $n=k+l$ mit $k\le l-1\Rightarrow k\le \frac{n-1}{2}$ verwendet. Koeffizientenvergleich ergibt den angegebenen Zusammenhang.

Die Schreibweise $G(z)$ für die erzeugende Funktion erlaubt auch die Darstellung

$f_n=\frac{1}{n!}\frac{{\mathrm{d}}^n}{\mathrm{d}{z}^n}G(0).$

Herleitung

In der Darstellung von $G(z)$ als unendliche Summe ist der Summand mit $k=0$ verzichtbar, siehe vorherige Herleitung. Die $n$-te Ableitung der erzeugenden Funktion ist mit der Potenzregel: $\frac{d^n}{d{z}^n}G(z)=$ $\sum _{k=1}^{\mathrm{\infty }}\frac{d^n}{d{z}^n}{f}_k{z}^k=$ $\sum _{k=1}^{n-1}\frac{d^n}{d{z}^n}{f}_k{z}^k+\frac{d^n}{d{z}^n}{f}_n{z}^n+\sum _{k=n+1}^{\mathrm{\infty }}\frac{d^n}{d{z}^n}{f}_k{z}^k=$ $0+n!f_n+\sum _{k=n+1}^{\mathrm{\infty }}\frac{k!}{(k-n)!}{f}_n{z}^{k-n}$ Für $z=0$ verschwindet die Summe der letzten Zeile. Für dieses $z$ entsteht mit Division durch $n!\ne 0$ die Behauptung.

Verbindung zum reziproken Wert der Zahl 89

Wertet man die erzeugende Funktion an der Stelle $x=1/10$ aus, so erhält man $10/89$, folglich lässt sich $89^{-1}$ in eine unendliche Summe von Fibonacci-Zahlen zur Basis $10^{-n-1}$ zerlegen.

$\begin{array}{cc}1/89& =0.0112359550\dots \\ & =0+1\cdot 10^{-2}+1\cdot 10^{-3}+2\cdot 10^{-4}+3\cdot 10^{-5}+5\cdot 10^{-6}+8\cdot 10^{-7}+13\cdot 10^{-8}+21\cdot 10^{-9}+\dots \end{array}$

Darstellung mit Matrizen

Die Fibonacci-Zahlen tauchen auch als Einträge der Potenzen der Matrix $A=\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)$ auf:

${\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)}^n=\left(\begin{array}{cc}{f}_{n+1}& f_n\\ f_n& f_{n-1}\end{array}\right)$

Aus der Relation $A^{m+n}=A^m{A}^n$ ergibt sich beispielsweise die erste oben angegebene Formel für $f_{m+n}$. $A$ beschreibt zugleich die Summationsvorschrift der Fibonacci-Folge, denn ihr Produkt mit einem Paar aufeinanderfolgender Fibonacci-Zahlen (als Spaltenmatrix geschrieben) ergibt das nächste Paar; entsprechend erzeugt $A^n$ das $n$-te Paar aus dem Startpaar $(0,1)$. Dies und die Tatsache, dass die Eigenwerte von $A$ gerade der Goldene Schnitt und dessen Kehrwert (Letzterer mit negativem Vorzeichen) sind, führen wieder auf die oben genannte Formel von Binet.

Verwandtschaft mit dem Pascalschen Dreieck

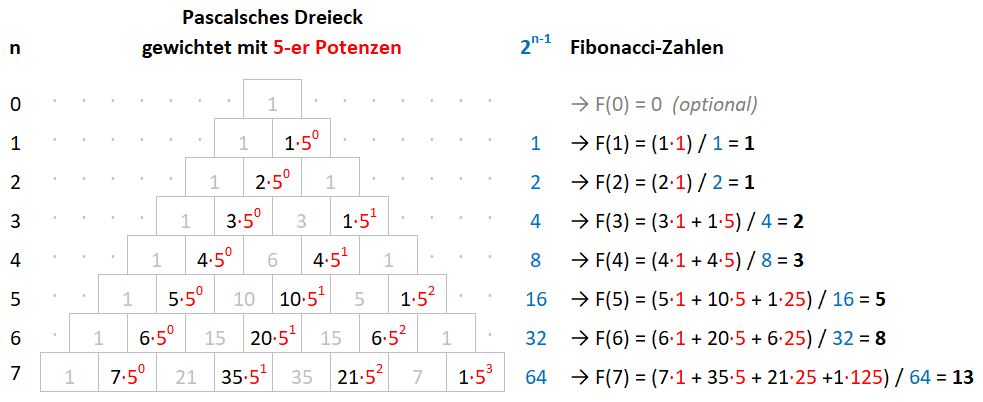
Die Fibonacci-Zahlen können mithilfe des Pascalschen Dreiecks beschrieben werden. Um die $n$-te Fibonacci-Zahl zu bestimmen, nimmt man aus der $n$-ten Zeile des Pascalschen Dreiecks jede zweite Zahl und gewichtet sie mit der entsprechenden Fünfer-Potenz – anfangend mit 0 in aufsteigender Reihenfolge, d. h. $5^0$, $5^1$, $5^2$ usw. Anschließend addiert man diese gewichteten Elemente zusammen und dividiert durch $2^{n-1}$.

Das Bild unten veranschaulicht die Berechnung der ersten sieben Fibonacci-Zahlen aus dem Pascalschen Dreieck. Zum leichteren Verständnis sind die nicht benutzten Elemente des Pascalschen Dreiecks im Bild ausgegraut, die Gewichtung mit den aufsteigenden Fünfer-Potenzen rot und die Exponenten $2^{n-1}$ cyan hervorgehoben.

Herleitung

Ausgehend von der expliziten Formel für die Fibonacci-Zahlen (s. Formel von Moivre-Binet weiter oben in diesem Artikel) $f_n=\frac{1}{\sqrt{5}}\cdot ({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n),n\ge 0$ kann man zunächst den Term $2^n$ im Nenner ausklammern und die verbliebene Differenz mittels Binomialkoeffizienten ausschreiben und anschließend zusammenfassen: $\begin{array}{cc}{f}_n& =\frac{1}{\sqrt{5}}\cdot \frac{1}{2^n}\cdot ({(1+\sqrt{5})}^n-{(1-\sqrt{5})}^n)\\ & =\frac{1}{\sqrt{5}}\cdot \frac{1}{2^n}\cdot (\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})1^{n-i}\cdot {\left(\sqrt{5}\right)}^i-\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})1^{n-i}\cdot {(-\sqrt{5})}^i)\\ & =\frac{1}{\sqrt{5}\cdot 2^n}\cdot \sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})\cdot ({\left(\sqrt{5}\right)}^i-{(-\sqrt{5})}^i)\\ \end{array}$ Für die Differenz unter dem Summenzeichen gilt ${\left(\sqrt{5}\right)}^i-{(-\sqrt{5})}^i=\{\begin{array}{cc}0& \text{falls }i\text{gerade}\\ 2\cdot {\left(\sqrt{5}\right)}^i& \text{falls }i\text{ungerade}\end{array},$ sodass man die Summe auf ungerade $i$ reduzieren kann: $\begin{array}{cc}{f}_n& =\frac{1}{\sqrt{5}\cdot 2^n}\cdot \sum _{j=0}^{\lfloor n/2\rfloor }(\genfrac{}{}{0ex}{}{n}{2j+1})\cdot 2\cdot {\left(\sqrt{5}\right)}^{2j+1}\\ & =\frac{1}{\sqrt{5}\cdot 2^n}\cdot \sum _{j=0}^{\lfloor n/2\rfloor }(\genfrac{}{}{0ex}{}{n}{2j+1})\cdot {\left(\sqrt{5}\right)}^{2j}\cdot 2\sqrt{5}\\ & =\frac{\sqrt{5}\cdot 2}{\sqrt{5}\cdot 2^n}\cdot \sum _{j=0}^{\lfloor n/2\rfloor }(\genfrac{}{}{0ex}{}{n}{2j+1})\cdot {\left({\left(\sqrt{5}\right)}^2\right)}^j\\ & =\frac{1}{2^{n-1}}\cdot \sum _{j=0}^{\lfloor n/2\rfloor }(\genfrac{}{}{0ex}{}{n}{2j+1})\cdot 5^j.\end{array}$ Der $\sqrt{5}$-Term kürzt sich also raus und unter dem Summenzeichen bleiben nur Fünfer-Potenzen. Das erklärt das scheinbare Paradoxon, dass die explizite Formel für Fibonacci-Zahlen mit ihren $\sqrt{5}$-Termen überhaupt ganze Zahlen liefert. Die Abrundung $\lfloor n/2\rfloor$ in der Summen-Obergrenze ist übrigens notwendig, damit die Indizierung nicht über den Wert $n$ hinausgeht und die ursprüngliche Summenbegrenzung eingehalten wird. Vergleicht man die unter dem Summenzeichen verbliebenen Binomialkoeffizienten mit denen im Pascalschen Dreieck, erkennt man, dass es sich dabei um jeden zweiten Koeffizienten in der entsprechenden Zeile des Dreiecks handelt (wie es im Bild oben visualisiert ist). Man kann die Formel also auch als $f_n=\frac{1}{2^{n-1}}\cdot \sum _{j=0}^{\lfloor n/2\rfloor }{P}_{n,2j+1}\cdot 5^j$ schreiben mit der Bezeichnung $P_{n,k}$ für einen Binomialkoeffizienten an der $k$-ten Stelle in der $n$-ten Zeile des Pascalschen Dreiecks (beide ab Null gezählt!). Als Beispiel erhält man für die 7-te Fibonacci-Zahl etwa den Wert $\begin{array}{cc}{f}_7& =\frac{1}{2^6}\cdot \sum _{j=0}^3{P}_{7,2j+1}\cdot 5^j\\ & =\frac{1}{64}\cdot (P_{7,1}\cdot 5^0+P_{7,3}\cdot 5^1+P_{7,5}\cdot 5^2+P_{7,7}\cdot 5^3)\\ & =\frac{1}{64}\cdot (7\cdot 1+35\cdot 5+21\cdot 25+1\cdot 125)=\frac{832}{64}=13.\end{array}$

Reihen von Reziproken

Da die Fibonacci-Zahlen exponentiell mit dem Index wachsen, konvergieren die reziproken Reihen absolut.

• Die unendliche Summe der Kehrwerte der Fibonacci-Zahlen mit geradem Index lässt sich mithilfe der Lambert-Reihe

$L(q):=\sum _{n=1}^{\mathrm{\infty }}\frac{q^n}{1-q^n}$   bei   $|q|<1$

ausdrücken:

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{f_{2n}}=\sqrt{5}\left[L\right({\mathrm{\Psi }}^2)-L({\mathrm{\Psi }}^4\left)\right]$

≈ 1,535370508836252985029852896651599

• Die unendliche Summe der Kehrwerte der Fibonacci-Zahlen mit ungeradem Index lässt sich durch eine Jacobische Thetafunktion ausdrücken:

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{f_{2n-1}}=\frac{\sqrt{5}}{4}\left[{\vartheta }_{10}\right({\mathrm{\Psi }}^2){]}^2$

≈ 1,824515157406924568142158406267328

• Ebenfalls geschlossen lässt sich die Formel für die Summe darstellen, wenn der Nenner um 1 erhöht wird:

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{1+f_{2n-1}}=\frac{\sqrt{5}}{2}$

• Die unendliche Summe der Kehrwerte aller Fibonacci-Zahlen

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{f_n}=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{f_{2n-1}}+\sum _{n=1}^{\mathrm{\infty }}\frac{1}{f_{2n}}$

≈ 3,359885666243177553172011302918927

ist irrational (André-Jeannin; 1989).

• Die unendliche Summe der Kehrwerte der Quadrate der Fibonaccizahlen findet sich bei Borwein:

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{{f_n}^2}=\frac{5}{24}\left\{\right[{\vartheta }_{10}\left({\mathrm{\Psi }}^2\right){]}^4-\left[{\vartheta }_{01}\right({\mathrm{\Psi }}^2){]}^4+1\}$

≈ 2,426320751167241187741569412926620

• Zudem zeigten Good (1974) und Hoggatt (1976):

$\sum _{n=0}^{\mathrm{\infty }}\frac{1}{f_{2^n}}=\frac{7-\sqrt{5}}{2}$

Verallgemeinerungen

Vorlage:Siehe auch Die klassische („kanonische“) Fibonacci-Folge ist durch drei Kriterien charakterisiert:

• Eine lineare Iteration, welche die beiden vorangehenden Folgenglieder einbezieht
• Eine Linearkombination dieser Folgenglieder, in der beide Vorgänger den Koeffizienten +1 tragen
• Beide Startglieder gleich +1

Jedes dieser Kriterien erlaubt eine Verallgemeinerung:

• Die Wahl anderer Startglieder $u$ und $v$ liefert eine Folge $(a_n)$, die mit der kanonischen Folge nach der Beziehung $a_n=u\cdot f_{n-2}+v\cdot f_{n-1}$ zusammenhängt. Ein Beispiel hierfür ist die Lucas-Folge $(L_n)$.

Für die Glieder einer solchen Folge gilt ein gegenüber der Formel von Moivre-Binet verallgemeinertes explizites Bildungsgesetz:

$a_n=\frac{k\cdot {\mathrm{\Phi }}^n-l\cdot {\mathrm{\Psi }}^n}{\sqrt{5}}$ mit $k=u\cdot {\mathrm{\Psi }}^2-v\cdot \mathrm{\Psi }$ und $l=u\cdot {\mathrm{\Phi }}^2-v\cdot \mathrm{\Phi }$.

Die kanonische Folge stellt sich hier als Spezialfall mit $u=v=1$ dar, was wegen der charakteristischen Gleichung sofort $k=1$ und $l=1$ liefert.

• Die Wahl anderer Koeffizienten für die Linearkombination liefert eine Folge, für die eine andere charakteristische Gleichung gilt. Eine Folge mit der Iterationsvorschrift

$a_n=q\cdot a_{n-2}+p\cdot a_{n-1}$

besitzt die charakteristische Gleichung $x^2-px-q=0$. Die Wurzeln dieser Gleichung bestimmen das explizite Bildungsgesetz. Wenn die charakteristische Gleichung die Wurzeln $\alpha$ und $\beta$ hat, dann lautet das Bildungsgesetz

$a_n=\frac{k\cdot {\alpha }^n-l\cdot {\beta }^n}{\alpha -\beta },$

wobei $k$ und $l$ wieder durch die Startglieder bestimmt sind.

• Eine Iteration, die mehr als zwei vorangehende Folgenglieder einbezieht, besitzt dementsprechend ein Polynom höheren Grades als charakteristische Gleichung, wobei die Wurzeln $x_i$ dieser Gleichung wieder im Bildungsgesetz auftauchen und die Koeffizienten $k_i$ durch die Anfangswerte bestimmt sind. Es gilt dann

$a_n=\sum _{i=1}^n{k}_i{x}_i^n$.

Beispiele für derartige Folgen sind die Tribonacci- und die Tetranacci-Folge. Die Perrin-Folge und die Padovan-Folge folgen der Regel $a_n=a_{n-2}+a_{n-3}$.

Eine Iteration, die nur das unmittelbar vorhergehende Glied verwendet, liefert in diesem Zusammenhang als entartete Fibonacci-Folge eine reine Potenzfolge.

Fibonacci-Folgen in der Natur

Phyllotaxis

Sonnenblume mit 34 und 55 Fibonacci-Spiralen

Anordnung gleich großer Kreise im Abstand des goldenen Winkels mit farblicher Markierung der Fibonacci-Spiralen 8, 13, 21, 34

Die Blätter (Phyllotaxis) oder Fruchtstände vieler Pflanzen sind in Spiralen angeordnet, wobei die Anzahl dieser Spiralen den Fibonacci-Zahlen entsprechen. In diesem Fall ist der Winkel zwischen architektonisch benachbarten Blättern oder Früchten bezüglich der Pflanzenachse der Goldene Winkel. Das liegt daran, dass Brüche von aufeinanderfolgenden Fibonacci-Zahlen den zugrunde liegenden Goldenen Schnitt am besten approximieren. Die Spiralen werden daher von Pflanzenelementen gebildet, deren Platznummern sich durch die Fibonacci-Zahl im Nenner unterscheiden und damit fast in die gleiche Richtung weisen. Durch diese spiralförmige Anordnung der Blätter um die Sprossachse erzielt die Pflanze die beste Lichtausbeute. Der Versatz der Blätter um das irrationale Verhältnis des Goldenen Winkels sorgt dafür, dass nie Perioden auftauchen, wie es z. B. bei 1/4 der Fall wäre (0° 90° 180° 270° | 0° 90° …). Dadurch wird der denkbar ungünstigste Fall vermieden, dass ein Blatt genau senkrecht über dem anderen steht und so die Blätter maximalen Schatten auf darunterliegenden Blättern erzeugen oder maximale „Lichtlücken“ entstehen.

Beispielsweise tragen die Körbe der Silberdistel (Carlina acaulis) hunderte gleichgestaltiger Blüten, die in kleineren Körben in einer 21-zu-55-Stellung, in größeren Körben in 34-zu-89- und 55-zu-144-Stellung in den Korbboden eingefügt sind. Auch die Schuppen von Fichtenzapfen wie auch von Ananasfrüchten bilden im und gegen den Uhrzeigersinn Spiralen, deren Schuppenanzahl durch zwei aufeinanderfolgende Fibonaccizahlen gegeben ist.

Wissenschaftshistorisch sei hier auf das Buch On Growth and Form von D’Arcy Wentworth Thompson (1917) verwiesen.

Stammbäume

Männchen der Honigbiene (Apis mellifera) werden als Drohnen bezeichnet. Interessanterweise beschreibt die Fibonacci-Folge die Anzahl der Ahnen einer Drohne. Das erklärt sich dadurch, dass eine Drohne (Generation n = 1) sich aus einem unbefruchteten Ei entwickelt, das ausschließlich Erbgut ihrer Mutter, der Bienenkönigin (Generation n = 2), enthält; eine Drohne hat keinen Vater. Eine Königin jedoch hat zwei Eltern, nämlich als Mutter eine andere Königin und als Vater eine Drohne (Generation n = 3) usw. Die Anzahl aller Ahnen einer Drohne in je einer so definierten n-ten Generation ist die n-te Fibonacci-Zahl $f_n$.

Um das einzusehen, lässt sich die Zeichnung zur Anzahl der Kaninchen in Fibonaccis Modell im Abschnitt Antike und Mittelalter in Europa verwenden. Jedes Paar nicht geschlechtsreifer Kaninchen entspricht einer Drohne, jedes Paar geschlechtsreifer Kaninchen einer Königin. In den Gleichungen der Modellierung ist dann $y_n$ die Anzahl der Drohnen, $x_n$ die Anzahl der Königinnen (jeweils in der n-ten Generation) und $f_{n>1}$ die Anzahl der Ahnen einer Drohne in der betrachteten Generation.

Fettsäuren

Unverzweigte aliphatische Monocarbonsäuren (hier: uaM), zu denen im Regelfall die Fettsäuren gehören, können verschieden viele Doppelbindungen an verschiedenen Positionen aufweisen. Die Anzahl der uaM gehorcht als Funktion der Kettenlänge der Fibonacci-Folge. Das folgt daraus, dass Doppelbindungen bei uaM nicht benachbart sind; die seltenen Ausnahmen sind hier vernachlässigt. Speziell gibt es nur eine aliphatische Monocarbonsäure mit einem C-Atom: Ameisensäure, eine mit zwei C-Atomen: Essigsäure, zwei mit dreien: Propionsäure und Acrylsäure usw. Bei 18 C-Atomen ergeben sich 2.584 Varianten (wovon Stearinsäure, Ölsäure, Linolsäure und Linolensäure vier Beispiele sind).

Auch hier lässt sich, um das einzusehen, die Zeichnung zur Anzahl der Kaninchen in Fibonaccis Modell im Abschnitt Antike und Mittelalter in Europa verwenden. Ein Kaninchenpaar der $n$-ten Generation entspricht dem $n$-ten Kohlenstoffatom einer uaM, wobei die Zählung bei der Carboxygruppe beginnt. Jedes Paar nicht geschlechtsreifer Kaninchen entspricht einem Kohlenstoffatom $c_n$, auf das keine Doppelbindung folgen kann, jedes Paar geschlechtsreifer Kaninchen einem Kohlenstoffatom $C_n$, auf das eine Doppelbindung folgen kann (oder nicht). Die Verbindungsstrecken von $c_n$ nach $C_{n+1}$ oder von $C_n$ nach $C_{n+1}$ entsprechen Einfachbindungen, die Verbindungsstrecken von $C_n$ nach $c_{n+1}$ Doppelbindungen. In den Gleichungen der Modellierung ist dann $y_n$ (bzw. $x_n$) die Anzahl der Kohlenstoffatome $c_n$ (bzw. $C_n$). – Jeder Pfad von $c_1$ zu einem Kohlenstoffatom der $n$-ten Generation entspricht genau einer uaM mit $n$ Kohlenstoffatomen; die Zuordnung ist bijektiv. Also ist die Anzahl $f_n$ der in der $n$-ten Generation betrachteten Kohlenstoffatome gleich der Anzahl der uaM mit $n$ Kohlenstoffatomen.

Geschichte

Berechnung der Kaninchen­aufgabe im Liber abbaci (am rechten Blattrand in roter Box von oben nach unten):
die Indizes beginnend mit der Gegenwart und endend mit (römisch) XII (Monaten);
jeweils darunter in hindu-arabischen Ziffern die (Fibonacci-)Zahlen 1, 2, 3, 5 bis 377 der Kaninchenpaare.

Altes Indien

Ihre früheste bekannte Erwähnung findet sich unter dem Namen mātrāmeru („Berg der Kadenz“) in der Chhandah-shāstra („Kunst der Prosodie“) des Sanskrit-Grammatikers Pingala (um 450 v. Chr. oder nach anderer Datierung um 200 v. Chr.). In ausführlicherer Form behandelten später auch Virahanka (6. Jh.) und besonders dann Acharya Hemachandra (1089–1172) diese Zahlenfolge, um die rechnerische Möglichkeit der Bildung von Metren durch regelmäßige Verteilung kurzer und langer Silben zu beschreiben.

Antike und Mittelalter in Europa

In der westlichen Welt war diese Folge ebenfalls schon in der Antike Nikomachos von Gerasa (um 100 n. Chr.) bekannt. Sie ist aber mit dem Namen des italienischen Mathematikers Fibonacci verbunden, der in seinem Liber abbaci („Buch der Rechenkunst“, Erstfassung von 1202 nicht erhalten, zweite Fassung von ca. 1227) diese Zahlenfolge mit dem Beispiel eines Kaninchenzüchters beschrieb, der herausfinden will, wie viele Kaninchenpaare innerhalb eines Jahres aus einem einzigen Paar entstehen, wenn jedes Paar ab dem zweiten Lebensmonat ein weiteres Paar pro Monat zur Welt bringt:

Die Anzahl der Kaninchen in Fibonaccis Modell bilden die Fibonacci-Zahlen (Baumdiagramm)

Kaninchen-Population in Fibonaccis Modell, erläutert anhand eines Säulendiagramms

Fibonacci illustrierte diese Folge durch die einfache mathematische Modellierung des Wachstums einer Population von Kaninchen nach folgenden Regeln:

1. Jedes Paar Kaninchen wirft pro Monat ein weiteres Paar Kaninchen.
2. Ein neugeborenes Paar bekommt erst im zweiten Lebensmonat Nachwuchs (die Austragungszeit reicht von einem Monat in den nächsten).
3. Die Tiere befinden sich in einem abgeschlossenen Raum („in quodam loco, qui erat undique pariete circumdatus“), sodass kein Tier die Population verlassen und keines von außen hinzukommen kann.

Fibonacci begann die Folge, nicht ganz konsequent, nicht mit einem neugeborenen, sondern mit einem trächtigen Paar, das seinen Nachwuchs bereits im ersten Monat wirft, sodass im ersten Monat bereits 2 Paare zu zählen sind. In jedem Folgemonat kommt dann zu der Anzahl der Paare, die im Vormonat gelebt haben, eine Anzahl von neugeborenen Paaren hinzu, die gleich der Anzahl derjenigen Paare ist, die bereits im vorvergangenen Monat gelebt hatten, da der Nachwuchs des Vormonats noch zu jung ist, um jetzt schon seinerseits Nachwuchs zu werfen. Fibonacci führte den Sachverhalt für die zwölf Monate eines Jahres vor (2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377) und wies auf das Bildungsgesetz der Folge durch Summierung jeweils zweier aufeinanderfolgender Folgenglieder (2+3 = 5, 3+5 = 8, 5+8 = 13 usw.) hin. Er merkte außerdem an, dass die Folge sich nach diesem Prinzip für eine unendliche Zahl von Monaten fortsetzen lässt, was dann allerdings unsterbliche Kaninchen voraussetzt: „et sic posses facere per ordinem de infinitis numeris mensibus.“ Weitere Beachtung hatte er dem Prinzip in seinen erhaltenen Werken nicht geschenkt.

Eine 2014 erschienene, mathematisch-historische Analyse zum Leben des Fibonacci, insbesondere zu seinem Aufenthalt in der nordafrikanischen Hafenstadt Bejaia (im heutigen Algerien), kam zu dem Schluss, dass der Hintergrund der Fibonacci-Folge gar nicht bei einem Modell der Vermehrung von Kaninchen zu suchen ist (was schon länger vermutet wurde), sondern vielmehr bei den Bienenzüchtern von Bejaia und ihrer Kenntnis des Bienenstammbaums zu finden ist. Zu Leonardos Zeit war Bejaia ein wichtiger Exporteur von Bienenwachs, worauf noch heute der französische Name der Stadt (Bougie, wie das frz. Wort für Kerze) hinweist.

Nachdem spätere Mathematiker wie Gabriel Lamé (1795–1870) die Entdeckung dieser Zahlenfolge für sich beansprucht hatten, brachten Édouard Lucas (1842–1891) und andere wieder in Erinnerung, dass der zu dieser Zeit älteste bekannte Beleg von Fibonacci stammte, und unter dem Namen „Fibonacci-Folge“ („suite de Fibonacci“, „Fibonacci sequence“, „successione di Fibonacci“) ist sie seither in den meisten westlichen Sprachen geläufig.

Mathematische Modellierung des Wachstums von Fibonaccis Kaninchen-Population Sei $x_n$ die Anzahl der geschlechtsreifen bzw. $y_n$ die Anzahl der nicht geschlechtsreifen Kaninchen der $n$-ten Generation, entsprechend für die Generationen $n-1$ und $n-2$. Nach den oben angegebenen Regeln ist mit diesen Bezeichnungen: $x_n=x_{n-1}+y_{n-1}$   (1) $x_{n-1}=x_{n-2}+y_{n-2}$   (1’) $y_n=x_{n-1}$ (2) Einsetzen von (1’) in (1) und anschließende Addition von (2) ergibt $x_n[+y_n]=(x_{n-2}+y_{n-2})+y_{n-1}[+x_{n-1}]$, für die Gesamtzahl $f_n=x_n+y_n$,  $f_{n-2}=x_{n-2}+y_{n-2}$,  $f_{n-1}=x_{n-1}+y_{n-1}$ von Kaninchen der jeweiligen Generation also $f_n=f_{n-2}+f_{n-1}$, was dem angegebenen rekursiven Bildungsgesetz der Fibonacci-Folge äquivalent ist. Mit $x_1=0,y_1=1$ beschreibt dieses Modell die in der Zeichnung angegebene Generationenfolge.

Neuzeit

Die Zahlentheoretiker Édouard Lucas und J. Wasteels (1865–1909) zeigten Jahrhunderte später, dass aufeinanderfolgende Fibonacci-Zahlen der Gleichung

$f_{n+1}^2-f_{n+1}{f}_n-f_n^2=(-1{)}^n$

genügen, und damit deren Bedeutung für die Zahlentheorie.

Bei der Fibonacci-Hyperbel

$x^2-xy-y^2=1$

sind

$(x,y)=(f_{2n+1},f_{2n})$

sowie bei der (nach geeigneter Transformation daraus erhaltenen) Gleichung

$x^2+y^2+1=3xy$

sind

$(x,y)=(f_{2n-1},f_{2n+1})$

die (einzigen) ganzzahligen Lösungen im 1. Quadranten.

Rezeption in Kunst und Unterhaltung

Fibonacci-Jingle für die Podcasts der Berliner Hochschule für Technik. Die ersten sieben Fibonacci-Zahlen als Melodie mit den Tonstufen in der Tonart C-Dur in physikalischer Stimmung (c = 2⁸ Hertz = 256 Hertz) mit reinen Intervallen.
Datei:BHT-Jingle.Bautsch.Klavier.Bautsch.430Hz.wav

In Kunst und Unterhaltung wird die Fibonacci-Folge als etwas Besonderes, im Medium noch nicht Dagewesenes aufgegriffen. Ihre mathematische Bedeutung bleibt dabei im Hintergrund.

• In der Unterhaltungsmathematik basieren das Schachbrett-Paradoxon und ähnliche geometrische Trugschlüsse auf den Eigenschaften der Fibonacci-Folge.
• Das Systemgedicht alfabet (1981) der dänischen Schriftstellerin Inger Christensen basiert auf der Fibonacci-Folge.
• Das Cover des Debütalbums der kanadischen Band The Organ, Grab That Gun, wurde von David Cuesta mithilfe eines auf der Fibonacci-Folge basierenden Rasters entworfen.
• Mario Merz hat sich seit den 1970er Jahren immer wieder mit der Fibonacci-Folge auseinandergesetzt. Seit 1992 hängt im Zürcher Hauptbahnhof seine Lichtskulptur Das philosophische Ei aus roten Neonröhren mit Tieren und Fibonacci-Zahlen. 2001 schuf er in Unna ein Lichtkunst-Objekt, die Fibonacci-Reihe, auf dem Schornstein einer ehemaligen Fabrik. In Zusammenarbeit mit Petra Paffenholz kreierte unter anderem das Kunstwerk „Ziffern im Wald“ auf dem Mönchsberg in Salzburg.
• Der Gesang im Lied Lateralus der Progressive-Metal-Band Tool basiert auf Fibonacci-Zahlen.
• Die Künstlerin Martina Schettina beschäftigt sich in ihren mathematischen Bildern ebenfalls mit den Fibonacci-Zahlen.
• Dan Brown verwendet in seinem Thriller The Da Vinci Code (2003) (deutsch: Sakrileg, 2004) die Fibonacci-Folge als geheime Botschaft.
• Im Film π – System im Chaos von Darren Aronofsky, in dem der Protagonist nach dem „Muster der Welt“ in den Kursdaten von Aktien und in der Zahl π sucht, wird die Fibonacci-Folge erwähnt.
• In der Serie Criminal Minds (Staffel 4, Folge 8) entführt ein Killer seine Opfer anhand der Fibonacci-Folge.
• In Lars von Triers Film Nymphomaniac wird im Kapitel 5 – kleine Orgelschule – die Fibonacci-Folge mit einem Bach-Orgelsatz in Verbindung gebracht.
• In dem Videospiel Watch Dogs von Ubisoft, in der Serienkiller-Mission als Zahlen, die an den einzelnen Tatorten der Opfer aufzufinden sind.
• In dem Song What’s Goes? von Die Orsons rappt KAAS die Fibonacci-Folge bis zur Zahl 144.
• Am Kernkraftwerk Leibstadt (CH) ist die Süd-Front des Maschinenhauses mit einer nach rechts progressiv ansteigenden Kurve aus sechs orangen Rechteckelementen bemalt, deren einzelne (aber auch addierte) Höhen der Fibonacci-Folge entsprechen.
• In dem Videospiel Dishonored: Death of the Outsider wird die Fibonacci-Folge als Kombination für einen Banktresor verwendet.
• In dem Manga Jojo’s Bizzare Adventure: Steel Ball Run wird die Fibonacci-Darstellung als Darstellung der Kraft des Protagonisten verwendet.
• In dem Kinderbuch Britta Tausendfuß von Irmela Wendt lernt das Mädchen Britta nach und nach zählen. Zuerst kann sie nur bis 5 zählen. Zum achten Geburtstag ihres Bruders schenkt sie ihm 8 Pferdchen aus Rübenschnitzeln. Als ihr Vater für den Bauernhof einen Traktor mit 13 PS anschafft, zählt sie 13 Gründe auf, warum das Familienpferd trotzdem 13 Mal besser ist. Der Buchtitel kommt daher, dass Britta für Zahlen, die ihr Verständnis übersteigen, einfach tausend sagt.
• Patric Sommerhoff hat die Fibonacci-Folge als Quadrat dargestellt und dabei den Goldenen Schnitt in Gestalt von Graustufen berücksichtigt

• Werke mit Fibonacci-Zahlen in Ziffern
• 
  Fibonacci-Zahlen
  im Zürcher Hauptbahnhof
• 
  Fibonacci-Zahlen auf dem Mönchsberg
  in Salzburg
• 
  Martina Schettina:
  Fibonaccis Traum, 2008, 40 cm

• Werke mit Verhältnissen in ihren Abmessungen mit Fibonacci-Zahlen
• 
  Petra Paffenholz:
  Fibonacci Cubes, 2014,
  1- bis 34-mal 2 dm Kantenlänge
• 
  Leuchtröhren im Cafè eines Kunstmuseums, 2019,
  je eine Leuchte bei Fibonacci-Zahl auf gedachter linearer Skala

Fibonacci-Datenstrukturen

Die Fibonacci-Folge ist namensgebend für folgende Datenstrukturen, bei deren mathematischer Analyse sie auftritt.

• Fibonacci-Baum
• Fibonacci-Heap

Verwandte der Fibonacci-Folge

Die Prinzipien der Fibonacci-Folge können auch auf ähnliche Zahlenfolgen angewendet werden. So besteht die Tribonacci-Folge gleichfalls aus aufeinanderaddierten Zahlen. Hierbei werden aber die drei vorangegangenen Zahlen addiert, um die jeweils nächste zu bilden:

$f_n=f_{n-1}+f_{n-2}+f_{n-3}$   für   $n\ge 4$

Die ersten Glieder lauten:

0, 1, 1, 2, 4, 7, …

Die Tribonaccizahlen tauchen bei einigen geometrischen Figuren auf.

Genau so, wie die Fibonaccizahlen aus 2 und die Tribonaccizahlen aus 3 Gliedern errechenbar sind, lassen sich die n-Bonaccizahlen (so auch Tetra- und Pentanaccizahlen) aus $n$ Gliedern bilden.

Die Stern-Brocot-Folge hat ein ähnliches Bildungsgesetz und weist ähnlich vielfältige mathematische Besonderheiten auf wie die Fibonacci-Folge.

Literatur

• Thomas Koshy: Fibonacci and Lucas Numbers with Applications. Wiley, 2001, ISBN 978-1-118-03131-5.
• Vorlage:AnkerVorlage:Literatur
• John H. Conway, Richard K. Guy: The Book of Numbers. Copernicus NY 1996, ISBN 0-387-97993-X.
• Richard A. Dunlap: The Golden Ratio and Fibonacci Numbers. 2. Auflage. World Scientific, Singapur, 1999, ISBN 981-02-3264-0.
• Huberta Lausch: Fibonacci und die Folge(n). Oldenbourg 2010, ISBN 978-3-486-58910-8.
• Paulo Ribenboim: The New Book of Prime Number Records. Springer-Verlag 1996, ISBN 0-387-94457-5.
• Vorlage:AnkerPaulo Ribenboim: Meine Zahlen, meine Freunde. Glanzlichter der Zahlentheorie. Springer-Lehrbuch, 2009, ISBN 978-3-540-87955-8.
• The Fibonacci Quarterly. Seit 1963 vierteljährlich erscheinende Zeitschrift, die sich der Fibonacci- und verwandten Folgen widmet.

Weblinks

• Vorlage:Webarchiv. – Sehr ausführliche Seite mit weiterführenden Themen.
• Fibonacci Numbers and the Golden Section. (englisch).
• Fibonacci und der Goldene Schnitt. (PDF; 823 kB).
• Albrecht Beutelspacher: Die Fibonacci-Zahlen. Aus der Fernsehsendung Mathematik zum Anfassen des Senders BR-alpha.
• Vorlage:TIBAV