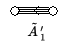Affine Lie-Algebra

Eine affine Lie-Algebra ist in der Mathematik eine unendlichdimensionale Lie-Algebra, die auf kanonische Weise aus einer endlichdimensionalen Lie-Algebra konstruiert wird. Dies ermöglicht die Konstruktion affiner Kac-Moody-Algebren.

Definition

Sei $𝔤$ eine endlich-dimensionale Lie-Algebra. Dann ist die zugehörige affine Lie-Algebra $\widehat{𝔤}$ definiert als der Vektorraum

$\widehat{𝔤}=𝔤\otimes ℂ[t,t^{-1}]\oplus ℂc$

mit der Kommutator-Relation

$[a\otimes t^n+\alpha c,b\otimes t^m+\beta c]=[a,b]\otimes t^{n+m}+⟨a,b⟩n{\delta }_{m+n,0}c$

für $a,b\in 𝔤,\alpha ,\beta \in ℂ,n,m\in \mathbb{Z}$. Hierbei bedeutet $[a,b]$ die Lie-Klammer in $𝔤$, $⟨a,b⟩$ die Killing-Form von $𝔤$ und $ℂ[t,t^{-1}]$ ist die assoziative Algebra der Laurent-Polynome.

$c$ ist ein Element des Zentrums der Liealgebra und $ℂc$ ist daher ein zentrales Ideal. Weiter hat man eine kurze exakte Sequenz

$0\to ℂc\to \widehat{𝔤}\to 𝔤\otimes ℂ[t,t^{-1}]\to 0$

von Lie-Algebren.

Erweiterte affine Lie-Algebra

Wir definieren durch die Formeln

$d(c):=0$

$d(a\otimes f):=a\otimes (t\frac{\mathrm{d}}{\mathrm{d}t})(f),a\in 𝔤,f\in ℂ[t,t^{-1}]$

eine Derivation auf $\widehat{𝔤}$. Beachte dazu, dass durch den Differentialoperator $t\frac{\mathrm{d}}{\mathrm{d}t}$ eine Derivation auf $ℂ[t,t^{-1}]$ erklärt ist. Die erweiterte affine Lie-Algebra $\widetilde{𝔤}$ entsteht aus $\widehat{𝔤}$ durch Adjunktion dieser Derivation, das heißt

$\widetilde{𝔤}:=ℂd⋉\widehat{𝔤}$,

wobei $⋉$ für die semidirekte Summe steht. Die so konstruierte Algebra $\widetilde{𝔤}$ heißt die zu $𝔤$ gehörige erweiterte affine Lie-Algebra oder einfach erweiterte affine Algebra.

Kac-Moody-Algebren affinen Typs

Aus den bekannten endlich-dimensionalen einfachen Lie-Algebren A_n, B_n, C_n, D_n, E₆, E₇, E₈, F₄, G₂ kann man mittels obiger Konstruktion die Kac-Moody-Algebren affinen Typs konstruieren, genauer die ungetwisteten Kac-Moody-Algebren affinen Typs. Weitere treten als Fixpunktalgebren gewisser Automorphismen auf, man spricht dann von getwisteten Kac-Moody-Algebren affinen Typs. Wir konstruieren im Folgenden sämtliche Kac-Moody-Algebren affinen Typs, die von unzerlegbaren verallgemeinerten Cartan-Matrizen herrühren. Dies sind sogenannte Realisierungen der abstrakt definierten Kac-Moody-Algebren, das heißt man erhält zu jeder Kac-Moody-Algebra affinen Typs mit unzerlegbarer, verallgemeinerter Cartan-Matrix einen konkreten Vektorraum mit einer Lie-Klammer wie oben angegeben, so dass diese Lie-Algebra der entsprechenden Isomorphieklasse angehört.

Ungetwistete Kac-Moody-Algebren affinen Typs

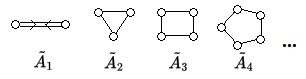
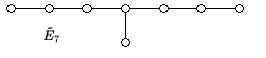
Für $𝔤$ wählen wir in obiger Konstruktion die endlichendimensionalen einfachen Lie-Algebren $A_n$, $B_n$, $C_n$, $D_n$, $E_6$, $E_7$, $E_8$, $F_4$, $G_2$, wobei die angegebenen Typen die einfache Lie-Algebra bis auf Isomorphie charakterisieren. Dann bezeichnet man die erweiterten affinen Lie-Algebren daraus mit ${\tilde{A}}_n$, ${\tilde{B}}_n$, ${\tilde{C}}_n$, ${\tilde{D}}_n$, ${\tilde{E}}_6$, ${\tilde{E}}_7$, ${\tilde{E}}_8$, ${\tilde{F}}_4$, ${\tilde{G}}_2$. Es handelt sich um Kac-MoodyAlgebren affinen Typs mit unzerlegbaren verallgemeinerten Cartan-Matrizen. Wir geben neben diesen auch die zugehörigen Dynkin-Diagramme an.

Typ	Verallgemeinerte Cartan-Matrix	Dynkin-Diagramm
${\tilde{A}}_n,n\ge 1$	$\left(\begin{array}{ccccccc}2& -1& & & & & -1\\ -1& 2& -1& & & & \\ & -1& .& .& & & \\ & & .& .& .& & \\ & & & .& .& -1& \\ & & & & -1& 2& -1\\ -1& & & & & -1& 2\end{array}\right)$
${\tilde{B}}_n,n\ge 3$	$\left(\begin{array}{ccccccc}2& & -1& & & & \\ & 2& -1& & & & \\ -1& -1& 2& -1& & & \\ & & -1& .& .& & \\ & & & .& .& -1& \\ & & & & -1& 2& -1\\ & & & & & -2& 2\end{array}\right)$
${\tilde{C}}_n,n\ge 2$	$\left(\begin{array}{ccccccc}2& -1& & & & & \\ -2& 2& -1& & & & \\ & -1& .& .& & & \\ & & -1& .& -1& & \\ & & & .& .& -1& \\ & & & & -1& 2& -2\\ & & & & & -1& 2\end{array}\right)$
${\tilde{D}}_n,n\ge 4$	$\left(\begin{array}{ccccccc}2& & -1& & & & \\ & 2& -1& & & & \\ -1& -1& .& .& & & \\ & & -1& .& -1& & \\ & & & .& .& -1& -1\\ & & & & -1& 2& \\ & & & & -1& & 2\end{array}\right)$
${\tilde{E}}_6$	$\left(\begin{array}{ccccccc}2& & & & -1& & \\ & 2& -1& & & & \\ & -1& 2& -1& & & \\ & & -1& 2& -1& -1& \\ -1& & & -1& 2& & \\ & & & -1& & 2& -1\\ & & & & & -1& 2\end{array}\right)$
${\tilde{E}}_7$	$\left(\begin{array}{cccccccc}2& & & & & & & -1\\ & 2& -1& & & & & \\ & -1& 2& -1& & & & \\ & & -1& 2& -1& & & \\ & & & -1& 2& -1& -1& \\ & & & & -1& 2& & \\ & & & & -1& & 2& -1\\ -1& & & & & & -1& 2\end{array}\right)$
${\tilde{E}}_8$	$\left(\begin{array}{ccccccccc}2& -1& & & & & & & \\ -1& 2& -1& & & & & & \\ & -1& 2& -1& & & & & \\ & & -1& 2& -1& & & & \\ & & & -1& 2& -1& & & \\ & & & & -1& 2& -1& -1& \\ & & & & & -1& 2& & \\ & & & & & -1& & 2& -1\\ & & & & & & & -1& 2\end{array}\right)$
${\tilde{F}}_4$	$\left(\begin{array}{ccccc}2& -1& & & \\ -1& 2& -1& & \\ & -1& 2& -1& \\ & & -2& 2& -1\\ & & & -1& 2\end{array}\right)$
${\tilde{G}}_2$	$\left(\begin{array}{ccc}2& -1& \\ -1& 2& -1\\ & -3& 2\end{array}\right)$

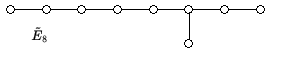Beachte, dass die Matrixgröße, das heißt die Zeilen- bzw. Spaltenzahl, um eins größer ist als der Index des Typnamens. Genauso verhält es sich mit der Anzahl der Knoten des zugehörigen Dynkin-Diagramms.

Getwistete Kac-Moody-Algebren affinen Typs

Die nicht-trivialen Automorphismen der Dynkin-Diagramme

Die weiteren Kac-Moody-Algebren affinen Typs können als Unteralgebren ungetwisteter Kac-Moody-Algebren konstruiert werden, genauer als Fixpunktalgebra eines Automorphismus. Im Folgenden sei $\sigma :𝔤\to 𝔤$ der Automorphismus, der zu einem der nebenstehend abgebildeten Graphautomorphismen der Dynkin-Diagramme zu $A_n$, $D_n$ und $E_6$ gehört. Eine Besonderheit tritt bei $D_4$ auf, hier gibt es einen zusätzliche Automorphismus der Ordnung 3, alle anderen Automorphismen haben offenbar die Ordnung 2. Dazu konstruieren wir nun Automorphismen $\tau$ auf den erweiterten affinen Lie-Algebren, indem wir definieren:

$\tau (a\otimes t^m)=e^{2\pi \mathrm{i}m/\mathrm{o}\mathrm{r}\mathrm{d}(\sigma )}\cdot \sigma (a)\otimes t^m$

$\tau (c)=c,\tau (d)=d$

Der skalare Faktor ist eine $\mathrm{o}\mathrm{r}\mathrm{d}(\sigma )$-te Einheitswurzel. Würde man statt dieser einfach 1 verwenden, so erhielte man auch Automorphismen, die aber nicht das Gewünschte leisten. Wegen der Einheitswurzel spricht man von getwisteten Automorphismen und nennt daher auch die Fixpunktalgebren

${𝔤}^{\tau }:=\{x\in 𝔤\mid \tau (x)=x\}$

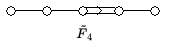
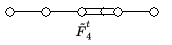
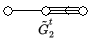
getwistete Algebren. Mittels dieser Konstruktion können die restlichen Kac-Moody-Algebren affinen Typs mit den Standardbezeichnungen ${\tilde{B}}_n^t$, ${\tilde{C}}_n^t$, ${\tilde{F}}_4^t$, ${\tilde{G}}_2^t$, ${{\tilde{A}}_1}^{\prime }$, ${{\tilde{C}}_n}^{\prime }$ konstruiert werden. Man verwendet dieselben Namen für die zugehörigen verallgemeinerten Cartan-Matrizen sowie für die zugehörigen Dynkin-Diagramme. Das hochgestellte t steht nicht für einen Automorphismus, sondern für Matrixtransposition.

Man erhält folgende Aufstellung:

Typ	Fixpunktalgebra	Verallgemeinerte Cartan-Matrix	Dynkin-Diagramm
${\tilde{B}}_n^t,n\ge 3$	${\tilde{A}}_{2n-1}^{\tau }$	$\left(\begin{array}{ccccccc}2& & -1& & & & \\ & 2& -1& & & & \\ -1& -1& .& .& & & \\ & & -1& .& -1& & \\ & & & .& .& -1& \\ & & & & -1& 2& -2\\ & & & & & -1& 2\end{array}\right)$
${\tilde{C}}_n^t,n\ge 2$	${\tilde{D}}_{n+1}^{\tau }$	$\left(\begin{array}{ccccccc}2& -2& & & & & \\ -1& 2& -1& & & & \\ & -1& .& -1& & & \\ & & .& .& .& & \\ & & & -1& .& -1& \\ & & & & -1& 2& -1\\ & & & & & -2& 2\end{array}\right)$
${\tilde{F}}_4^t$	${\tilde{E}}_6^{\tau }$	$\left(\begin{array}{ccccc}2& -1& & & \\ -1& 2& -1& & \\ & -1& 2& -2& \\ & & -1& 2& -1\\ & & & -1& 2\end{array}\right)$
${\tilde{G}}_2^t$	${\tilde{D}}_4^{\tau }$	$\left(\begin{array}{ccc}2& -1& \\ -1& 2& -3\\ & -1& 2\end{array}\right)$
${{\tilde{A}}_1}^{\prime }$	${\tilde{A}}_2^{\tau }$	$\left(\begin{array}{cc}2& -1\\ -4& 2\end{array}\right)$
${{\tilde{C}}_n}^{\prime },n\ge 2$	${\tilde{A}}_{2n}^{\tau }$	$\left(\begin{array}{ccccccc}2& -2& & & & & \\ -1& 2& -1& & & & \\ & -1& .& -1& & & \\ & & .& .& .& & \\ & & & .& .& -1& \\ & & & & -1& 2& -2\\ & & & & & -1& 2\end{array}\right)$

Für die Größen der Matrizen und Dynkin-Diagramme gilt das für die ungetwisteten Algebren Gesagte. Ferner beachte, dass ${\tilde{D}}_4^{\tau }$ in obiger Liste zweimal vorkommt. Es handelt sich bei den zwei Fällen um verschiedene Automorphismen $\tau$, für ${\tilde{G}}_2^t$ wird der Autorphismus des oben genannten Sonderfalls für $D_4$ verwendet, für ${\tilde{D}}_{n+1}^{\tau }$ mit $n=3$ ist es der Automorphismus, der nur die zwei Enden des Dynkin-Diagramms austauscht.