Zwei-Personen-Nullsummenspiel

Ein Zwei-Personen-Nullsummenspiel ist in der Spieltheorie ein Nullsummenspiel mit zwei Spielern. Nullsummenspiele sind dadurch gekennzeichnet, dass die Verluste der Verlierer genau den Gewinnen der Sieger entsprechen. Die meisten gängigen Spiele um Geld, wie Skat, Poker usw., sind Beispiele hierfür. Sind an einem Nullsummenspiel nur zwei Spieler beteiligt, so entfallen auch alle Möglichkeiten für kooperatives Verhalten auf Kosten Dritter. Aus diesem Grund stellen Zwei-Personen-Nullsummenspiele ein gut überblickbares Modell für spieltheoretische Strategie- und Gleichgewichtskonzepte dar, das schon seit Beginn der Spieltheorie regelmäßig untersucht wurde. Als Besonderheit fallen hier die Begriffe Nash-Gleichgewicht, Gleichgewicht in Maximin-Strategien und Gleichgewicht in Minimax-Strategien zusammen.

Die Begriffe Maximin- und Minimax-Strategie werden in der Literatur allerdings nicht einheitlich verwendet, es sollte immer angegeben werden, welches inhaltliche Konzept damit verbunden ist: Strategie schlimmstmöglicher Bestrafung des Gegners (in diesem Artikel Minimax) oder Maximierung des ungünstigsten Ergebnisses (in diesem Artikel Maximin).

Der Artikel definiert die grundlegenden Begriffe und behandelt die zwei zentralen Sätze für die Bestimmung der Gleichgewichte. Die Konzepte werden anhand der Beispiele „Matching Pennies“ und „Schere, Stein, Papier“ erläutert.

Definitionen

Spiel in Normalform

Um ein Spiel in Normalform (Spieltheorie) zu beschreiben, legt man fest, welche Spieler am Spiel beteiligt sind; man bezeichnet dies als die Spielermenge $I$. Jedem Spieler $i\in I$ wird eine Strategiemenge $S_i$ zugeordnet. Die Strategiemenge $S_i$ enthält alle Strategien, aus denen Spieler $i$ bei Durchführung des Spiels eine Strategie $s_i$ auswählt. Schließlich gibt es für jeden Spieler $i\in I$ eine Auszahlungsfunktion $u_i$, die jeder Strategiekombination $(s_j{)}_{j\in I}$ eine Auszahlung für Spieler $i$ zuordnet.

Definition: Unter einem Spiel $\mathrm{\Gamma }$ in Normalform versteht man ein Tripel $(I,(S_i{)}_{i\in I},(u_i{)}_{i\in I})$, wobei $u_i:\prod _{j\in I}{S}_j\to ℝ$.

Konstantsummenspiel

Bei einem Konstantsummenspiel wird bei jeder Strategiekombination, also jedem Spielergebnis die gleiche Auszahlungssumme $C$ an alle Spieler ausgeschüttet.

Definition: Ein Spiel $\mathrm{\Gamma }=(I,(S_i{)}_{i\in I},(u_i{)}_{i\in I})$ heißt Konstantsummenspiel mit Auszahlungssumme $C$, wenn gilt: $\sum _{i\in I}{u}_i=C$.

Konstantsummenspiele ergeben sich insbesondere, wenn ein fester Ressourcenbestand oder ein fester Geldbetrag unter den Spielern als Spielergebnis aufgeteilt wird.

Nullsummenspiel

Definition: Ein Konstantsummenspiel mit Auszahlungssumme $C$ heißt Nullsummenspiel, wenn: $C=0$.

Spieltheoretisch besteht kein wesentlicher Unterschied zwischen Konstantsummen- und Nullsummenspielen: Aus einem Konstantsummenspiel $\mathrm{\Gamma }$ mit Auszahlung $C$ entsteht ein äquivalentes Nullsummenspiel $\tilde{\mathrm{\Gamma }}$, indem man einem beliebigen Spieler $i$ vor Spielbeginn den Betrag $C$ zuordnet, den er nach Spielende sicher verliert und somit ${\tilde{u}}_i:=u_i-C$ erhält. Die Auszahlungen im Spiel $\tilde{\mathrm{\Gamma }}$ summieren sich dann zu 0. Aus diesem Grund kann man sagen, dass die Gewinne der Sieger den Verlusten der Unterlegenen entsprechen.

Zwei-Personen-Nullsummenspiel

Definition: Ein Nullsummenspiel $(I,(S_i{)}_{i\in I},(u_i{)}_{i\in I})$ heißt Zwei-Personen-Nullsummenspiel, wenn: $|I|=2$.

Bei Zwei-Personen-Nullsummenspielen ist die Auszahlung des zweiten Spielers bereits vollständig durch die Auszahlung des ersten Spielers festgelegt: Bezeichnet man die beiden Spieler mit $1$ und $2$, also $I=\{1,2\}$, so gilt $u_2(s_1,s_2)=-u_1(s_1,s_2)$.

Es ist daher möglich, die Definition eines Zwei-Personen-Nullsummenspiels zu vereinfachen:

Definition: Ein Zwei-Personen-Nullsummenspiel ist ein Tripel $(S_1,S_2,u)$, wobei $u:S_1\times S_2\to ℝ$.

Die Spielermenge $I$ ist hierbei natürlicherweise $I=\{1,2\}$; die Auszahlungsfunktion $u$ bezieht sich auf Spieler 1, Spieler 2 hat dann die Auszahlungsfunktion $u_2:=-u$.

Beispiele

Zwei-Personen-Nullsummenspiele, bei denen jeder Spieler nur endlich viele Strategien hat, werden gerne in Form einer Bimatrix oder vereinfacht als Matrix dargestellt. Dabei entspricht jede Zeile einer Strategie $s_1$ für Spieler 1, also einem Element aus $S_1$, jede Spalte entsprechend einer Strategie $s_2$ für Spieler 2. In den Feldern der Bimatrix stehen die Auszahlungen $u_1(s_1,s_2)$ und $u_2(s_1,s_2)$. Die Bimatrix stellt also eine Wertetabelle der Funktionen $u_1$ und $u_2$ gemäß der ersten Definition eines Zwei-Personen-Nullsummenspiels dar.

Da die Auszahlung von Spieler 2 aber durch die Auszahlung von Spieler 1 bereits eindeutig festgelegt ist, genügt eigentlich die Angabe der Auszahlung für Spieler 1; dies führt zur Matrixdarstellung gemäß der 2. Definition. Die Matrix ist dann eine Wertetabelle für die Funktion $u$.

$\mathrm{\Gamma }$ als Bimatrix

	$s_2^1$	$\cdots$	$s_2^n$
$s_1^1$	$u_1(s_1^1,s_2^1)$ , $u_2(s_1^1,s_2^1)$	$\cdots$	$u_1(s_1^1,s_2^n)$, $u_2(s_1^1,s_2^n)$
$⋮$	$⋮$	$\ddots$	$⋮$
$s_1^m$	$u_1(s_1^m,s_2^1)$, $u_2(s_1^m,s_2^1)$	$\cdots$	$u_1(s_1^m,s_2^n)$, $u_2(s_1^m,s_2^n)$

In der vereinfachten Darstellung erhält man dann:

$\begin{array}{cccc}\mathrm{\Gamma }& s_2^1& \cdots & s_2^n\\ s_1^1& u_{(}{s}_1^1,s_2^1)& \cdots & u_{(}{s}_1^1,s_2^n)\\ ⋮& ⋮& \ddots & ⋮\\ s_1^m& u_{(}{s}_1^m,s_2^1)& \cdots & u_{(}{s}_1^m,s_2^n)\end{array}$

Als Matrix des Spiels bezeichnet man dann die $m\times n$-Matrix A:

$A=\left(\begin{array}{ccc}u(s_1^1,s_2^1)& \cdots & u(s_1^1,s_2^n)\\ ⋮& \ddots & ⋮\\ u(s_1^m,s_2^1)& \cdots & u(s_1^m,s_2^n)\end{array}\right)$

Matching Pennies (A)

In der Spieltheorie wird häufig Matching-Pennies als Nullsummenspiel betrachtet: Zwei Spieler legen gleichzeitig eine Münze auf den Tisch. Liegt bei beiden Münzen Kopf (K) oder bei beiden Münzen Zahl (Z) oben, so gehören die beiden Münzen Spieler 1; zeigen die beiden Münzen verschiedene Seiten, so gehören die beiden Münzen Spieler 2. Da der Sieger also die Münze des Verlierers gewinnt, handelt es sich um ein Nullsummenspiel. Als Bimatrix ergibt sich folgende Darstellung:

Auszahlungsmatrix für Spieler 1 und Spieler 2

	Kopf	Zahl
Kopf	1 , −1	−1, 1
Zahl	−1 , 1	1 , −1

In der vereinfachten Darstellung erhält man folgende Matrix:

$\begin{array}{ccc}& K& Z\\ K& 1& -1\\ Z& -1& 1\end{array}\text{also die Matrix}A=\left(\begin{array}{cc}1& -1\\ -1& 1\end{array}\right)$ Vorlage:Siehe auch

Schere, Stein, Papier (B)

In Deutschland verbreiteter ist „Schere, Stein, Papier“. Die Strategien in diesem Spiel heißen wie der Name des Spiels. Man verbindet damit die Vorstellung, dass die Schere (S) kaputt geht, wenn man versucht, mit ihr einen Stein (St) zu zerschneiden, wohingegen die Schere das Papier (P) problemlos in Stücke schneidet. Mit dem Papier kann man den Stein einwickeln. Daraus ergibt sich, dass Schere gegen Papier, Papier gegen Stein und Stein gegen Schere gewinnt. Bei gleicher Strategie beider Spieler kommt es zu einem Unentschieden. Für die spieltheoretische Behandlung wird meistens Sieg mit einem Punktgewinn, Unentschieden mit 0 und Niederlage mit einem Punktverlust gewertet.

Die Strategiemengen der Spieler lauten also $S_1=S_2=\{S,St,P\}$. Die Menge aller möglichen Strategiekombinationen (Kartesisches Produkt) ist dann:

$S_1\times S_2=\{(S,S),(S,St),(S,P),(St,S),(St,St),(St,P),(P,S),(P,St),(P,P)\}$.

In Form einer Bimatrix sieht das Spiel dann folgendermaßen aus:

Auszahlungsmatrix für Spieler 1 und Spieler 2

	Schere	Stein	Papier
Schere	0, 0	-1, 1	1, -1
Stein	1, -1	0, 0	-1, 1
Papier	-1, 1	1, -1	0, 0

In der vereinfachten Matrixdarstellung sieht „Schere, Stein, Papier“ dann so aus:

$\begin{array}{cccc}& S& St& P\\ S& 0& -1& 1\\ St& 1& 0& -1\\ P& -1& 1& 0\end{array}\text{also die Matrix}B=\left(\begin{array}{ccc}0& -1& 1\\ 1& 0& -1\\ -1& 1& 0\end{array}\right)$

Weitere Beispiele (C), (D)

Für die weitere Diskussion sollen noch die folgenden beiden Spiele (C) und (D) eingeführt werden. Bei Beispiel (C) sehen wir ein Nullsummenspiel, das ein Nash-Gleichgewicht in reinen Strategien enthält, welches in der Rubrik Lösungskonzepte gelöst wird. (D) ist das Spiel Matching Pennies, bei dem gemischte Strategien gewählt werden können.

Auch Spiel (C) wird zunächst als Bimatrix und dann als Matrix angegeben.

Auszahlungsmatrix für Spieler 1 und Spieler 2

	Links	Mitte	Rechts
Oben	−2, 2	0, 0	−3, 3
Unten	3, −3	2, −2	4, −4

$\begin{array}{cccc}& l& m& r\\ o& -2& 0& -3\\ u& 3& 2& 4\end{array}\text{also}C=\left(\begin{array}{ccc}-2& 0& -3\\ 3& 2& 4\end{array}\right)$

Das Beispiel (D) zeigt ein Spiel, bei dem die Strategiemengen der Spieler nicht endlich sind; es handelt sich hier bei den Strategiemengen der Spieler um das Einheitsintervall $[0,1]$, also ein Kontinuum.

(D) $\mathrm{\Gamma }=(S_1,S_2,u)$ mit $S_1=S_2=[0,1]$ und $u:[0,1]\times [0,1]\to ℝ,u(s_1,s_2)=(2s_1-1)(2s_2-1)$.

Gleichgewichtskonzepte

Die Gleichgewichtskonzepte werden hier nur für Zwei-Personen-Nullsummenspiele definiert.

Nash-Gleichgewicht

Ein zentraler Begriff der Spieltheorie ist die beste Reaktion eines Spielers auf eine gegnerische Strategiekombination. Im 2-Personen-Spiel ist dies die Antwort auf die Frage, mit welcher Strategie ein Spieler seine Auszahlung maximiert, wenn die gegnerische Strategie vorgegeben ist. Die Reaktionsfunktion oder auch Reaktionskorrespondenz eines Spielers gibt also für jede gegnerische Strategie an, was die beste strategische Antwort darauf ist; der Begriff Reaktionskorrespondenz ist die Menge aller besten Antworten auf die gegnerische Strategie.

Definition: Die Reaktionskorrespondenz $R_1(s_2)$ von Spieler 1 auf Spieler 2 ist die mengenwertige Funktion $R_1(s_2)={\text{argmax}}_{s_1\in S_1}{u}_1(s_1,s_2)$.

Man beachte, dass bei der vereinfachten Darstellung in der Definition einer besten Reaktion für Spieler 2 minimiert statt maximiert wird:

Definition: Die Reaktionskorrespondenz $R_2(s_1)$ von Spieler 2 auf Spieler 1 ist die mengenwertige Funktion $R_2(s_1)={\text{argmin}}_{s_2\in S_2}u(s_1,s_2)$.

Unter einem Nash-Gleichgewicht versteht man eine Strategienkombination, bei der jeder Spieler seine Auszahlung für die gegebene Strategie des Gegners maximiert, also jeder Spieler eine beste Reaktion auf den Gegner spielt. Für ein Zwei-Personen-Nullsummenspiel in Normalform bedeutet dies folgendes:

Definition: Die Strategiekombination $(s_1^{*},s_2^{*})$ ist ein Nash-Gleichgewicht, wenn gilt: $s_1^{*}\in {\text{argmax}}_{s_1\in S_1}{u}_1(s_1,s_2^{*})\text{und}{s}_2^{*}\in {\text{argmax}}_{s_2\in S_2}{u}_2(s_1^{*},s_2)$.

Die Definition verändert sich für die vereinfachte Darstellung $(S_1,S_2,u)$ zu:

Definition: Die Strategiekombination $(s_1^{*},s_2^{*})$ ist ein Nash-Gleichgewicht, wenn gilt: $s_1^{*}\in {\text{argmax}}_{s_1\in S_1}u(s_1,s_2^{*})\text{und}{s}_2^{*}\in {\text{argmin}}_{s_2\in S_2}u(s_1^{*},s_2)$.

Minimax

Man kann auch unterstellen, dass die Spieler im Wesentlichen daran interessiert sind, den Gewinn ihres Gegners möglichst gering zu halten. Für Spieler 1 bedeutet dies, dass er eine Strategie mit folgender Definition wählt:

Definition: Die Strategie $s_1^{*}$ ist eine Minimax-Strategie für Spieler 1, wenn gilt: $s_1^{*}\in {\text{argmin}}_{s_1\in S_1}\underset{s_2\in S_2}{\max }{u}_2(s_1,s_2)$.

In der vereinfachten Darstellung $(S_1,S_2,u)$ wird daraus:

Definition: Die Strategie $s_1^{*}$ ist eine Minimax-Strategie für Spieler 1, wenn gilt: $s_1^{*}\in {\text{argmax}}_{s_1\in S_1}\underset{s_2\in S_2}{\min }u(s_1,s_2)$.

Dies erklärt, warum die Begriffe Minimax- und Maximin-Strategie (Min-Max-Theorem) in der Literatur nicht einheitlich verwendet werden.

Eine Minimax-Strategie im Sinne der hier gegebenen Definition wird auch als Strategie schlimmstmöglicher Bestrafung bezeichnet. Spieler 1 kann also durch eine Minimax-Strategie sicherstellen, dass Spieler 2 höchstens $-\underset{s_1\in S_1}{\max }\underset{s_2\in S_2}{\min }u(s_1,s_2)$ erhält. Da es sich um ein Nullsummenspiel handelt, bedeutet dies, dass Spieler 1 also mindestens $V_1=\underset{s_1\in S_1}{\max }\underset{s_2\in S_2}{\min }u(s_1,s_2)$ gewinnt.

Für Spieler 2 gilt bei Anwendung einer Minimax-Strategie, dass er mit einer Minimax-Strategie den Gewinn von Spieler 1 auf $V_2=\underset{s_2\in S_2}{\min }\underset{s_1\in S_1}{\max }u(s_1,s_2)$ beschränken kann. Es gilt also $V_1\le V_2$. Falls $V_1=V_2$ gilt, so spricht man von einem Gleichgewicht in Minimax-Strategien.

Maximin

Sind die Spieler sehr pessimistisch, so gehen sie davon aus, dass es bei jeder Strategie, die sie wählen, zum für sie ungünstigsten Ergebnis kommt. Sie sollten dann versuchen dieses Minimalergebnis zu optimieren. Dies führt zu folgender Definition:

Definition: Die Strategie $s_1^{*}$ ist eine Maximin-Strategie für Spieler 1, wenn gilt: $s_1^{*}\in {\text{argmax}}_{s_1\in S_1}\underset{s_2\in S_2}{\min }{u}_1(s_1,s_2)$.

In der vereinfachten Darstellung $(S_1,S_2,u)$ wird daraus:

Definition: Die Strategie $s_1^{*}$ ist eine Maximin-Strategie für Spieler 1, wenn gilt: $s_1^{*}\in {\text{argmax}}_{s_1\in S_1}\underset{s_2\in S_2}{\min }u(s_1,s_2)$.

Vergleicht man die zweite Definitionsvariante mit der Definition einer Minimax-Strategie, so erkennt man, dass bei Zwei-Personen-Nullsummenspielen kein Unterschied besteht.

Die Definitionen von $V_1$, $V_2$ und der Gleichgewichtsbegriff übertragen sich ebenfalls und stimmen mit den unter Minimax eingeführten Begriffen überein; von einem Gleichgewicht in Maximin-Strategien spricht man also nur, falls $V:=V_1=V_2$. Wenn ein Gleichgewicht vorliegt, so bezeichnet man mit $V:=V_1=V_2$ den Wert des Spiels. $V$ ist der Gewinn für Spieler 1 und der Verlust für Spieler 2, wenn sie das Spiel durchführen; die Bezeichnung Wert des Spiels bezieht sich auf die Sicht von Spieler 1.

Allgemein nennt man $V_1$ unteren Spielwert und $V_2$ oberen Spielwert des Spiels.

Die Tatsache, dass bei Zwei-Personen-Nullsummenspielen kein Unterschied zwischen Minimax- und Maximin-Strategien besteht, verbunden mit der Tatsache, dass einige Autoren die Reihenfolge der Anwendung der Optimierungsoperatoren, andere Autoren jedoch die Reihenfolge im Schriftbild für maßgeblich halten, und nicht zuletzt, dass statt einer Gewinnauszahlung auch gerne eine Verlustfunktion als Spielergebnis verwendet wird, führt dazu, dass man sich auf die Bedeutung der Begriffe Minimax und Maximin nicht verlassen kann. Entscheidend ist vielmehr, ob die Strategiewahl auf der schlimmstmöglichen Bestrafung des Gegners, oder auf der Minimierung des eigenen Maximalverlusts beruht. Im Bereich der Zwei-Personen-Nullsummenspiele ist diese Unterscheidung aber belanglos.

Zusammenhang zwischen den Konzepten

Die enge Beziehung zwischen Minimax- und Maximin-Gleichgewichten bei Zwei-Personen-Nullsummenspielen ergibt sich bereits aus den Definitionen. Es gilt aber sogar der folgende Satz, der die Äquivalenz aller drei Konzepte sichert.

Satz: In einem Zwei-Personen-Nullsummenspiel $(S_1,S_2,u)$ stimmen die Mengen der Nash-Gleichgewichte, der Gleichgewichte in Minimax-Strategien und der Gleichgewichte in Maximin-Strategien überein.

Die Voraussetzung, dass es sich um ein Zwei-Personen-Nullsummenspiel handelt, ist dabei entscheidend. Im Allgemeinen fallen bereits die Begriffe „beste Reaktion“, „Minimax-Strategie“ und „Maximin-Strategie“ nicht zusammen. Für die konkrete Berechnung von Gleichgewichten in 2 Personen-Nullsummenspielen bedeutet der Satz, dass es genügt, die Gleichgewichte nach einem beliebigen der drei Konzepte zu ermitteln.

Lösungskonzepte

Endliche Strategiemengen

Bei endlicher Strategiemenge lassen sich die besten Reaktionen, Minimax- und Maximin-Strategien durch Ausprobieren finden. Anschließend kann man ebenfalls durch Ausprobieren feststellen, ob es sich um ein Gleichgewicht handelt.

In Beispiel (C) gilt $S_1=\{o,u\}$ und $S_2=\{l,m,r\}$. In der Matrix wird die beste Reaktion von Spieler 1 auf Spieler 2 durch eine Unterstreichung, die beste Reaktion von Spieler 2 auf Spieler 1 durch einen Strich über der Zahl gekennzeichnet. Falls also Spieler 1 o spielt, sollte Spieler 2 mit r antworten, daher erhält die $-3$ eine Überstreichung. Das Matrixfeld $(u,m)$ ist gleichzeitig beste Reaktion für beide Spieler und somit ein Nash-Gleichgewicht. Da es keine weiteren derartigen Matrixfelder gibt, handelt es sich bei $(u,m)$ um das einzige Nash-Gleichgewicht dieses Spiels. Im Nash-Gleichgewicht erhält Spieler 1 eine Auszahlung von $2$, Spieler 2 eine Auszahlung von $-2$.

$\begin{array}{cccc}(C)& l& m& r\\ o& -2& 0& -\bar{3}\\ u& \underset{\_}{3}& \overline{\underset{\_}{2}}& \underset{\_}{4}\end{array}$

Bei „Matching Pennies“ (A) sehen die besten Reaktionen so aus:

$\begin{array}{ccc}(A)& K& Z\\ K& \underset{\_}{1}& -\bar{1}\\ Z& -\bar{1}& \underset{\_}{1}\end{array}$

Keine der Strategiekombinationen stellt ein Nash-Gleichgewicht dar, da nie beide eine beste Reaktion auf die gegnerische Strategie spielen.

Zur Ermittlung der Maximin-Strategien für Spieler 1 bestimmt man zunächst die Zeilenminima ZMin, siehe letzte Spalte.

$\begin{array}{cccc}(A)& K& Z& ZMin\\ K& 1& -1& -1\\ Z& -1& 1& -1\end{array}$

Beide Zeilenminima sind gleich groß, so dass sowohl K als auch Z eine Maximin-Strategie für Spieler 1 darstellen. Es gilt $V_1=-1$; Spieler 1 kann also sicherstellen, dass er nicht mehr als 1 verliert. Für Spieler 2 müssen analog die Spaltenmaxima SpMax ermittelt werden:

$\begin{array}{ccc}(A)& K& Z\\ K& 1& -1\\ Z& -1& 1\\ SpMax& 1& 1\end{array}$

Auch für ihn sind beide Strategien Maximin-Strategien; es gilt $V_2=1$. Nun ist aber $V_2>V_1$, so dass auch kein Gleichgewicht in Maximin-Strategien vorliegt.

Bei „Schere, Stein, Papier“ liegen ähnliche Verhältnisse wie bei „Matching Pennies“ vor:

$\begin{array}{ccccc}(B)& S& St& P& ZMin\\ S& 0& -\bar{1}& \underset{\_}{1}& -1\\ St& \underset{\_}{1}& 0& -\bar{1}& -1\\ P& -\bar{1}& \underset{\_}{1}& 0& -1\\ SpMax& 1& 1& 1& \end{array}$

Auch die Bestimmung der Maximin-Strategien führt wieder zu dem Ergebnis, dass für jeden Spieler jede seiner Strategien eine Maximin-Strategie ist; es gilt auch hier: $1=V_2>V_1=-1$.

„Matching Pennies“ und „Schere, Stein, Papier“ haben also kein Gleichgewicht in der Menge der vorgegebenen Strategiekombinationen. Um dieses Manko zu beheben, führt man gemischte Strategien ein.

Gemischte Strategien

Definition: Unter einer gemischten Strategie für Spieler 1 in einem Spiel $(S_1,S_2,u)$ versteht man eine Wahrscheinlichkeitsverteilung über der Strategienmenge $S_1$.

Lässt man für beide Spieler gemischte Strategien zu, so entsteht ein erweitertes Nullsummenspiel, bei dem jeder Spieler die Wahrscheinlichkeiten für seine Strategien wählt. Zur besseren Unterscheidung bezeichnet man die Strategien aus $S_1$ bzw. $S_2$ als reine Strategien der Spieler. Es handelt sich hierbei um besondere gemischte Strategien, bei denen eine Strategie aus $S_i$ die Wahrscheinlichkeit 1 trägt. Möchte man betonen, dass keine Strategie die Wahrscheinlichkeit 1 trägt, so spricht man von einer echt gemischten Strategie.

Als Auszahlung $u$ für das erweiterte Nullsummenspiel nimmt man den Erwartungswert, der sich ergibt, wenn man davon ausgeht, dass die Wahrscheinlichkeitsverteilungen der Spieler unabhängig sind.

Für Matching Pennies führt dies zu folgender Erweiterung auf gemischte Strategien: Es sei $s_i\in [0,1]$ die Wahrscheinlichkeit, dass Spieler $i$ Kopf wählt. Bei Unabhängigkeit ergeben sich dann die folgenden Wahrscheinlichkeiten für die verschiedenen Strategiekombinationen:

$\begin{array}{ccc}P(s_1,s_2)& K& Z\\ \text{HLINE TBD}K& s_1{s}_2& s_1(1-s_2)\\ Z& (1-s_1)s_2& (1-s_1)(1-s_2)\end{array}$

Als Erwartungswert $U$ für die Auszahlung erhält man dann:

$U(s_1,s_2)=s_1{s}_2\cdot 1+s_1(1-s_2)\cdot (-1)+(1-s_1)s_2\cdot (-1)+(1-s_1)(1-s_2)\cdot 1=(2s_1-1)(2s_2-1)$.

Vergleicht man dies mit Beispiel (D) so sieht man, dass (B) gerade die Erweiterung von Matching Pennies auf gemischte Strategien darstellt ($u=U$).

Bezeichnet man allgemein die Wahrscheinlichkeiten, die Spieler 1 für seine reinen Strategien aus $S_1=\{s_1^1,s_1^2...,s_1^m\}$ wählt, mit $x=(x_1,x_2,...,x_m{)}^T$ und ebenso die Wahrscheinlichkeiten für Spieler 2 mit $y=(y_1,y_2,...,y_n{)}^T$, so lässt sich $U=E[u]$ als Matrizenprodukt schreiben; $A$ bezeichnet hierbei die Auszahlungsmatrix des Spiels:

$U=x^{T}Ay$.

Um eine beste Reaktion von Spieler 1 auf die gemischte Strategie $y=(y_1,y_2,...,y_n{)}^T$ von Spieler 2 zu finden, muss also das lineare Optimierungsproblem

${\text{argmax}}_{x\in {ℝ}^m}{x}^{T}Ay$    unter der Nebenbedingung    ${\sum }_{i=1}^m{x}_i=1,x_i\ge 0$ gelöst werden.

Umgekehrt findet man eine beste Reaktion von Spieler 2 auf die gemischte Strategie $x=(x_1,x_2,...,x_m{)}^T$ von Spieler 1, indem man folgendes lineare Optimierungsproblem löst:

${\text{argmin}}_{y\in {ℝ}^n}{x}^{T}Ay$    ${\sum }_{j=1}^n{y}_j=1,y_j\ge 0$.

Eine Maximin-Strategie (bei Zwei-Personen-Nullsummenspielen äquivalent zur Minimax-Strategie) für Spieler 1 findet man, indem man folgendes Optimierungsproblem löst:

${\text{argmax}}_{x\in {ℝ}^m}{\text{min}}_{y\in {ℝ}^n}{x}^{T}Ay$    unter der Nebenbedingung    ${\sum }_{i=1}^m{x}_i=1,x_i\ge 0,{\sum }_{j=1}^n{y}_j=1,y_j\ge 0$.

Umgekehrt muss man für eine Maximin-Strategie von Spieler 2 folgendes Optimierungsproblem lösen:

${\text{argmin}}_{y\in {ℝ}^n}{\text{max}}_{x\in {ℝ}^m}{x}^{T}Ay$    unter der Nebenbedingung    ${\sum }_{i=1}^m{x}_i=1,x_i\ge 0,{\sum }_{j=1}^n{y}_j=1,y_j\ge 0$.

Die Existenz von Gleichgewichten nach der Erweiterung auf gemischte Strategien wird durch das folgende Minimax-Theorem von John von Neumann (1928) sichergestellt:

Satz: Es sei $A$ eine reelle $m\times n$-Matrix. Dann existiert ein Tripel $(x^{*},y^{*},V)$, so dass

${x^{*}}^{T}Ay\ge V\mathrm{\forall }y$ und

$x^{T}A{y}^{*}\le V\mathrm{\forall }x$.

Hierbei stehen $x$ bzw. $x^{*}$ für Wahrscheinlichkeitsverteilungen über die $m$ Zeilen von $A$, $y$ bzw. $y^{*}$ für Wahrscheinlichkeitsverteilungen über die $n$ Spalten von $A$.

Damit hat jedes Zwei-Personen-Nullsummenspiel mit endlichen Strategiemengen für beide Spieler mindestens ein Gleichgewicht in gemischten Strategien. Jede gleichgewichtige bzw. Minimax- oder Maximin-Strategie eines Spielers bildet mit jeder gleichgewichtigen bzw. Minimax- oder Maximin-Strategie des anderen Spielers (in der Erweiterung des Spiels auf gemischte Strategien) ein Gleichgewicht.

Beispiele (Fortsetzung)

Matching Pennies

Es sollen nun für „Matching Pennies“ (A) die Maximin-Strategien für Spieler 1 in gemischten Strategien ermittelt werden:

Zunächst muss für jede vorgegebene Strategie ${\bar{s}}_1$ von Spieler 1 seine minimale Auszahlung bestimmt werden, die sich durch optimales Verhalten von Spieler 2 ergibt:

${\text{min}}_{s_2\in [0,1]}u({\bar{s}}_1,s_2)$.

Es gilt:

$u({\bar{s}}_1,s_2)={\bar{s}}_1{s}_2-{\bar{s}}_1(1-s_2)-(1-{\bar{s}}_1)s_2+(1-{\bar{s}}_1)(1-s_2)=1-2{\bar{s}}_1+(4{\bar{s}}_1-2)s_2$.

Für die Minimierung bezüglich $s_2$ kommt es nur darauf an, ob der Ausdruck $4{\bar{s}}_1-2$ in der letzten Klammer positiv, Null oder negativ ist. Dieser Ausdruck ist positiv, falls ${\bar{s}}_1>\frac{1}{2}$. Dann wird das Minimum für $s_2=0$ erreicht, und beträgt $1-2{\bar{s}}_1$. Der Ausdruck in der Klammer ist negativ, falls ${\bar{s}}_1<\frac{1}{2}$. Dann wird das Minimum für $s_2=1$ erreicht, und beträgt $-1+2{\bar{s}}_1$. Der Ausdruck in der Klammer ist Null, falls ${\bar{s}}_1=\frac{1}{2}$, $s_2$ hat dann keinen Einfluss auf das Minimum, $u({\bar{s}}_1,s_2)$ ist dann unabhängig von $s_2$ immer 0.

Grafik

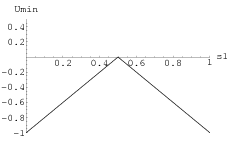
Damit lässt sich ${\text{min}}_{s_2\in [0,1]}u({\bar{s}}_1,s_2)$ wie folgt schreiben:

$U_{\min }({\bar{s}}_1):={\text{min}}_{s_2\in [0,1]}u({\bar{s}}_1,s_2)=\{\begin{array}{cc}-1+2{\bar{s}}_1& \text{für}{\bar{s}}_1<\frac{1}{2}\\ 1-2{\bar{s}}_1& \text{für}{\bar{s}}_1\ge \frac{1}{2}\end{array}$

Somit erhält man für die Bestimmung der Maximin-Strategie für Spieler 1 folgendes Optimierungsproblem:

${\text{argmax}}_{s_1\in [0,1]}\underset{s_2\in [0,1]}{\min }u(s_1,s_2)={\text{argmax}}_{s_1\in [0,1]}{U}_{\min }(s_1)$.

$U_{\min }$ ist streng monoton steigend auf dem Intervall $[0,\frac{1}{2}]$ und streng monoton fallend auf dem Intervall $[\frac{1}{2},1]$; das Maximum von $U_{\min }$ liegt also bei $s_1^{*}=\frac{1}{2}$. Dies ist also die eindeutige Maximin-Strategie für Spieler 1 in gemischten Strategien. Aus Symmetriegründen gibt es auch nur eine Maximin-Strategie für Spieler 2, nämlich $s_2^{*}=\frac{1}{2}$.

Der Wert des Spiels beträgt $V=0$. Aufgrund des Äquivalenzsatzes ist dies auch das einzige Nash-Gleichgewicht und auch das einzige Gleichgewicht in Minimax-Strategien.

Schere, Stein, Papier

Für „Schere, Stein, Papier“ argumentiert man wie folgt. Falls Spieler 1 nicht alle drei reinen Strategien mit der gleichen Wahrscheinlichkeit spielt, so kann Spieler 2 durch Wahl einer geeigneten Strategie dafür sorgen, dass die erwartete Auszahlung von Spieler 1 negativ wird. Es sei zum Beispiel $p_1:=P(S)\ge P(St)\ge P(P)=:p_3$, wobei mindestens eine der Ungleichungen strikt ist. Insbesondere ist dann $p_1>p_3$. Wenn Spieler 2 jetzt „Stein“ spielt, so ist die erwartete Auszahlung von Spieler 1 $Eu=p_1\cdot (-1)+p_3\cdot 1=p_3-p_1<0$.

Wählt Spieler 1 hingegen alle drei Wahrscheinlichkeiten gleich $\frac{1}{3}$, also $x^T=\left(\begin{array}{ccc}\frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right)$, so ist seine erwartete Auszahlung 0 für jede gemischte Strategie von Spieler 2. Seine erwartete Auszahlung ist dann nämlich:

$\mathrm{E}(u)=x^{T}Ay=[x^{T}A]y=\left[\left(\begin{array}{ccc}\frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right)\left(\begin{array}{ccc}0& -1& 1\\ 1& 0& -1\\ -1& 1& 0\end{array}\right)\right]\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right)=\left(\begin{array}{ccc}0& 0& 0\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right)=0$.

Falls die Wahrscheinlichkeiten bei Spieler 1 auf Schere, Stein und Papier in anderer Größenreihenfolge verteilt sind, so gilt eine analoge Argumentation, falls Spieler 2 die Strategie mit der mittleren Wahrscheinlichkeit spielt.

Zu jeder von $x^T=\left(\begin{array}{ccc}\frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right)$ verschiedenen Strategie existiert also eine Strategie von Spieler 2, die Spieler 1 eine negative Auszahlung liefert. Somit ist $x^T=\left(\begin{array}{ccc}\frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right)$ die eindeutige Maximin-Strategie von Spieler 1.

Aus Symmetriegründen gilt das auch für Spieler 2. Damit ist diese Strategiekombination das einzige gemischte Gleichgewicht und der Wert des Spiels ist $V=0$.

Literatur

• Avinash K. Dixit, Barry J. Nalebuff: Spieltheorie für Einsteiger. Schäffer Poeschl, Stuttgart 1997, ISBN 3-7910-1239-8.
• Christian Rieck: Spieltheorie. Eine Einführung. Christian Rieck Verlag, 1993, S. 102–104.
• Diether Coenen: Quasi-Nullsummenspiele und dominierte Gleichgewichtspunkte in Bimatrix-Spielen. Westdeutscher Verlag, 1967.
• G. Owen: Spieltheorie. Springer-Verlag, 1971.
• Morton D. Davis: Spieltheorie für Nichtmathematiker. Oldenbourg Verlag, 1993, S. 15–35, doi:10.1524/9783486836103
• Burkhard Rauhut, Norbert Schmitz, Ernst-Wilhelm Zachow: Spieltheorie. Teubner, Stuttgart 1979, ISBN 3-519-02351-2.
• Sylvain Sorin: A First Course on zero-sum Repeated Games. Springer, 2002.
• Thomas Riechmann: Spieltheorie. Verlag Franz Vahlen, 2002, S. 63–67.
• Werner Krabs: Spieltheorie. Teubner, Wiesbaden 2005.