Schmetterlingsgraph

Datenflussdiagramm von den beiden Eingängen x_0,1 zu den beiden Ausgängen y_0,1, welche der Kontur eines Schmetterlings entspricht

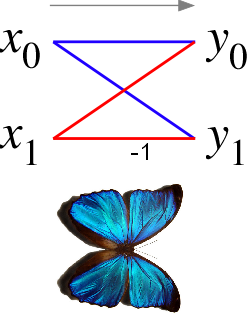
Ein Schmetterlingsgraph (Vorlage:EnS) zeigt, wie aus der Grundfunktion (der Schmetterling) der Fourier-Transformation ein schneller Fouriertransformator (FFT, schnelle Fourier-Transformation) aufgebaut wird.

Der Begriff Schmetterling leitet sich im Datenflussdiagramm von der Darstellung der beiden Dreiecke ab, die bei der Darstellung des Grundelementes (time decimation butterfly) der schnellen Fouriertransformation entstehen. Ein Schmetterling bewerkstelligt (jeweils komplex) eine Multiplikation, eine Subtraktion und eine Addition im Rahmen des FFT-Algorithmus von Cooley und Tukey. Durch die Linien wird angezeigt, dass die beiden Ausgänge $y_0$ und $y_1$ von den beiden Eingängen $x_0$ und $x_1$ abhängen.

Im einfachsten Fall (radix-2 Cooley und Tukey FFT-Algorithmus) besteht der Schmetterlingsgraph nur aus den dargestellten zwei Ein- und Ausgängen:

$y_0=x_0+x_1$

$y_1=x_0-x_1$

Der allgemeine Fall mit $n=2^p$ Eingängen resultiert in einer Anzahl von $O(n\log n)$ an Schmetterlingsgraphen mit den Bezügen:

$y_0=x_0+x_1{\omega }^k$

$y_1=x_0-x_1{\omega }^k$

mit

$\omega =\exp (-\frac{2\pi \mathrm{i}k}{n})$,

dem Index $k$ und der imaginären Einheit $\mathrm{i}$.

Literatur

• Vorlage:Literatur
• Vorlage:Literatur