Quandle

Ein Quandle ist in der Mathematik eine algebraische Struktur, die vor allem in der Knotentheorie Anwendung findet.

Definition

Ein Quandle ist eine Menge $Q$ mit einer Operation $▹$, so dass für alle $x,y,z\in Q$ gilt:

(i) $x▹x=x$

(ii) die durch $f_y(x)=x▹y$ definierte Abbildung $f_y:Q\to Q$ ist eine Bijektion

(iii) $(x▹y)▹z=(x▹z)▹(y▹z)$.

Bedingung (iii) heißt Selbstdistributivität.

Weil $f_y$ eine Bijektion ist, gibt es eine inverse Abbildung $f_y^{-1}:Q\to Q$. Die Operation ${▹}^{-1}$ wird für $x,y\in Q$ durch

$x{▹}^{-1}y:=f_y^{-1}(x)$

definiert.

Reidemeister-Bewegungen

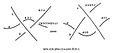
Die Quandle-Operationen lassen sich mittels der Reidemeister-Bewegungen von Knotendiagrammen interpretieren:

• 
  Reidemeister I
• 
  Reidemeister II
• 
  Reidemeister III

Beispiele

• Jede abelsche Gruppe $A$ ist ein Quandle mit der Operation

$x▹y=2y-x$.

• Für eine Gruppe $G$ und $n\in \mathbb{N}$ definiert man den Quandle $Con{j}_n(G)$ als die Menge $G$ mit der Operation

$x▹y=y^{-n}x{y}^n$.

• Für eine Gruppe $G$ definiert man den Quandle $Core(G)$ als die Menge $G$ mit der Operation

$x▹y=y{x}^{-1}y$.

• Jeder $\mathbb{Z}\left[t^{\pm 1}\right]$-Modul ist ein Quandle mit der Operation

$x▹y=tx+(1-t)y$.

Diese Quandle werden als Alexander-Quandle bezeichnet.

• Der Fundamentalquandle eines Knotens (oder allgemeiner einer Verschlingung) $K\subset S^3$ ist definiert wie folgt. Sei $X_K=S^3\setminus int(N(K))$ das Komplement einer regulären Umgebung und $x_0\in \partial X_K$. Definiere

$Q(K)={\pi }_1(C(K),\partial C(K),x_0)$

mit der (wohldefinierten) Verknüpfung

$\left[{\gamma }_1\right]▹\left[{\gamma }_2\right]=[{\gamma }_2\circ m_{{\gamma }_2(1)}\circ {\gamma }_2^{-1}\circ {\gamma }_1]$,

wobei $m_{{\gamma }_2(1)}$ den Meridian durch ${\gamma }_2(1)$ bezeichnet.

Literatur

• David Joyce: A classifying invariant of knots, the knot quandle. J. Pure Appl. Algebra 23 (1982), no. 1, 37–65.
• Sergei Matwejew: Distributive groupoids in knot theory. (russisch) Mat. Sb. (N.S.) 119(161) (1982), no. 1, 78–88, 160.

Weblinks

• Scott Carter: A Survey of Quandle Ideas