Partielle Autokorrelationsfunktion

Geschätzte partielle Autokorrelation der Zeitreihe der Tiefen des Huronsee. Die zugehörigen Konfidenzintervalle sind in blau (um die 0 zentriert) gezeichnet.

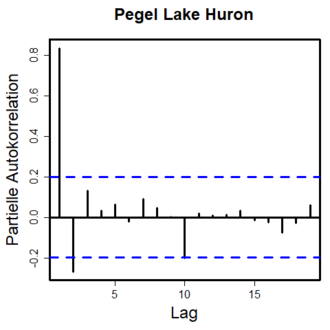
Die partielle Autokorrelationsfunktion (PAKF, engl. PACF) ist wie die Autokovarianzfunktion und die Autokorrelationsfunktion ein Instrument, um Abhängigkeiten zwischen den Werten einer Zeitreihe zu unterschiedlichen Zeiten zu identifizieren. Die PAKF misst den linearen Zusammenhang zwischen $Y_t$ und $Y_{t+k}$ unter Ausschaltung des Einflusses der dazwischen liegenden Variablen.

Bei autokorrelierten stationären Prozessen enthalten die Beobachtungen $Y_t$ bis $Y_{T-1}$ Informationen über den erwarteten Betrag und Vorzeichen der Größe $Y_T$ (mit $t<T\in \mathbb{N}$). Die partielle Autokorrelation drückt dann die bedingte Information über die Ausprägung von $Y_T$ aus, die man erhält, wenn man darüber hinaus $Y_{t-1}$, den Zustand des Prozesses zur Zeit $t-1$, kennt.

Mithilfe dieser bedingten Betrachtung der PACF kann, im Gegensatz zur Autokorrelationsfunktion, die Ordnung eines Autoregressiver Prozesses direkt bestimmt werden.

Definition bedingte Korrelation

Die formale Definition lautet bei zentrierten stationären Zeitreihen

${\phi }_{kk}:=\mathrm{Corr}(Y_t,Y_{t-k}|Y_{t-1},\cdots ,Y_{t-k+1})k=0,\pm 1,\pm 2,\cdots$

Die Operation $\mathrm{Corr}(\cdot ,\cdot |\cdot )$ bezeichnet dabei die bedingte Korrelation, gebildet mit der bedingten Erwartungswerten und bedingten Varianzen

$\mathrm{Corr}(W,Z|{ℱ}_t):=\frac{E(WZ|{ℱ}_t)-E(W|{ℱ}_t)E(Z|{ℱ}_t)}{\sqrt{\mathrm{Var}(W|{ℱ}_t)\mathrm{Var}(Z|{ℱ}_t)}}.$

Die Funktion ist in $k$ symmetrisch und ihre Werte liegen im Intervall $[-1,1]$. Es gilt ${\phi }_{00}=1$.

Beachte die bedingte Korrelation stimmt nur dann mit der partiellen Korrelation überein, falls die Zufallsvariablen multivariat normal verteilt, elliptisch verteilt, multivariat hypergeometrisch verteilt, multivariat negative hypergeometrische verteilt, multinomial verteilt oder Dirichlet verteilt sind.

Verfahren

Zur Bestimmung der PAKF gibt es verschiedene Verfahren:

• Yule-Walker-Gleichungen (nach George Udny Yule),
• Durbin-Levinson-Algorithmus.

Letztere Methode geht rekursiv vor. Mit ihr kann auch eine empirische PAKF (geschätzte PAKF) berechnet werden. Eine Approximation der Standardabweichung der empirischen PAKF ist mit der Quenouille-Approximation möglich:

$\hat{\sigma }({\hat{\phi }}_{kk})\approx \frac{1}{\sqrt{T}}$.

Siehe auch

• Partieller Korrelationskoeffizient

Quellen

• Box, G. E. P., Jenkins, G. M., und Reinsel, G. C. (1994). Time Series Analysis, Forecasting and Control, 3rd ed. Prentice Hall, Englewood Clifs, NJ.