Datei:Kalman Polynom vs GLS.svg
Aus testwiki
Zur Navigation springen
Zur Suche springen

Größe der PNG-Vorschau dieser SVG-Datei: 540 × 288 Pixel. Weitere Auflösungen: 320 × 171 Pixel | 640 × 341 Pixel | 1.024 × 546 Pixel | 1.280 × 683 Pixel | 2.560 × 1.365 Pixel.
Originaldatei (SVG-Datei, Basisgröße: 540 × 288 Pixel, Dateigröße: 44 KB)
Diese Datei stammt aus Wikimedia Commons und kann von anderen Projekten verwendet werden. Die Beschreibung von deren Dateibeschreibungsseite wird unten angezeigt.
Beschreibung
| BeschreibungKalman Polynom vs GLS.svg |
English: Kalman filter comparted to generalized least square estimation
Deutsch: Kalman-filter im Vergleich mit einer Schätzung mit generalisierten kleinsten Quadraten |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Physikinger |
| SVG‑Erstellung InfoField | |
| Quelltext InfoField | Python code# This source code is public domain
# Autor: Christian Schirm
import numpy
import matplotlib.pyplot as plt
# Generate polynomial
nSteps = 121
coeff = [-50, 70, -16, 1]
sigmaNoise = 50
sigmaPrior = 100
xMax = 10
ts = numpy.linspace(0,xMax,nSteps)
deltaT = ts[1] - ts[0]
nPoly = len(coeff)
A = numpy.array([ts**i for i in range(nPoly)])
y_polynomial = coeff @ A
# Noise
numpy.random.seed(1)
noise = sigmaNoise*numpy.random.randn(nSteps)
# Add noise to the signal
y = y_polynomial + noise
# Prepare Kalman estimation
D = numpy.zeros((nPoly,nPoly))
D[(numpy.arange(nPoly-1), numpy.arange(nPoly-1)+1)] = 1
Dt = D*deltaT
F = numpy.identity(nPoly) + Dt + Dt @ Dt/2 + Dt @ Dt @ Dt/6
H = numpy.zeros((1,nPoly))
H[0,0] = 1
# Initialize Kalman estimation
x = numpy.zeros(nPoly)
P = sigmaPrior**2 * numpy.identity(nPoly)
# Start Kalman iteration
yEst = []
ySigma = []
for i in range(len(y)):
# Propagate
if i > 0:
x = F @ x
P = F @ P @ F.T
# Estimate
K = P @ H.T @ numpy.linalg.inv(H @ P @ H.T + sigmaNoise**2)
x = x + K @ (y[i] - H @ x)
P = (numpy.identity(nPoly) - K @ H) @ P
ySigma.append(P[0,0])
yEst.append(x[0])
ySigma = numpy.sqrt(ySigma)
# Select prior state for GLS estimation
p = numpy.ones(nPoly)/sigmaPrior
p[2] *= 2
p[3] *= 6
# Iterative GLS estimation
yLSI = []
for i in range(nSteps):
nm = min(nPoly, i+1)
RN = numpy.zeros((i+1,i+1))
RN[numpy.diag_indices(RN.shape[0])] = 1/sigmaNoise**2
RI = numpy.zeros((nm,nm))
RI[numpy.diag_indices(RI.shape[0])] = p[:nm]**2
Ai = A[:nm,:i+1]
cLS = numpy.linalg.inv(Ai @ RN @ Ai.T + RI) @ Ai @ RN @ y[:i+1]
yLSI.append(cLS @ Ai[:,i])
# Plot
plt.figure(figsize=(6,3.2))
#plt.fill_between(ts,y_polynomial-ySigma, y_polynomial+ySigma, color='0.2', alpha=0.17, label='Konfidenzintervall', lw=0)
#plt.plot(ts,y,'.-', color='C1', markersize=4, linewidth=0.4, alpha=0.6, label='Polynom + Rauschen')
plt.plot(ts,y_polynomial,'C2', label='Polynom 3. Grades')
plt.plot(ts,yEst,'c-', color='#2f97ff', label='Kalman-Schätzung')
# please not that yLS is not defined in this code! the code will therefore result in an error, the following line should be commented out or the calculation of yLS must be included.
plt.plot(ts,yLS,'k-', alpha=0.25, label='Kleinste-Quadrate-Schätzung (ohne a-priori)')
plt.plot(ts,yLSI,'C3--' ,label='Kleinste-Quadrate-Schätzung (mit a-priori)')
plt.xlabel('Zeit')
plt.legend(loc=4)
plt.tight_layout()
plt.savefig('Kalman_Polynom_vs_GLS.svg')
plt.savefig('Kalman_Polynom_vs_GLS.png')
#plt.show()
|
Lizenz
Ich, der Urheber dieses Werkes, veröffentliche es unter der folgenden Lizenz:
| Diese Datei wird unter der Creative-Commons-Lizenz CC0 1.0 Verzicht auf das Copyright zur Verfügung gestellt. | |
| Die Person, die das Werk mit diesem Dokument verbunden hat, übergibt dieses weltweit der Gemeinfreiheit, indem sie alle Urheberrechte und damit verbundenen weiteren Rechte – im Rahmen der jeweils geltenden gesetzlichen Bestimmungen – aufgibt. Das Werk kann – selbst für kommerzielle Zwecke – kopiert, modifiziert und weiterverteilt werden, ohne hierfür um Erlaubnis bitten zu müssen.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Kurzbeschreibungen
Kalman-Filter Vergleich mit generalisierten kleinsten Quadraten
Kalman filter vs. generalized least square estimation
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
1. Februar 2022
image/svg+xml
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 23:02, 1. Feb. 2022 | 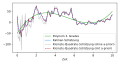 | 540 × 288 (44 KB) | wikimediacommons>Physikinger | Uploaded own work with UploadWizard |
Dateiverwendung
Die folgende Seite verwendet diese Datei: