Datei:01 Siebzehneck-1818-Animation.gif
Diese Datei stammt aus Wikimedia Commons und kann von anderen Projekten verwendet werden. Die Beschreibung von deren Dateibeschreibungsseite wird unten angezeigt.
Beschreibung
| Beschreibung01 Siebzehneck-1818-Animation.gif |
Deutsch: Siebzehneck, Weiterführung der Basiskonstruktion aus dem Jahr 1818, mit Ergänzung von OK als mittlere Proportionale von OH und OQ, Animation
English: Heptadecagon, continuation of the basic construction from 1818, with addition of OK as a mean proportional between OH and OQ, animation |
| Datum | |
| Quelle | Basic construction: T. P. Stowell of Rochester, N. Y., The Analyst: A Monthly Journal of Pure And Applied Mathematicus Vol.1, p. 94–95 |
| Urheber | Basic construction: T. P. Stowell, derivative work: continuation of the basic construction Petrus3743 |
| Andere Versionen |
 Heptadecagon, continuation of the basic construction from 1818, with addition of OK as a mean proportional between OH and OQ |
Konstruktionsbeschreibung (deutsch)
(Freie Übersetzung der Beschreibung)
T. P. Stowell of Rochester, N. Y. schreibt:
„Um ein regelmäßiges Polygon von siebzehn Seiten im Kreis zu konstruieren. Zeichnen Sie den Radius CO rechtwinklig zum Durchmesser AB: Für OQ nehmen Sie die Hälfte von OC und für OD den achten Teil vom Radius OB: Nehmen Sie für DE und für DF jeweils gleich DQ, für EG gleich EQ und FH gleich FQ; für OK nehmen Sie die mittlere Proportionale zwischen OH und OQ[1] und ziehen Sie KM durch K parallel zu AB, KM trifft in M auf den über OG beschriebenen Halbkreis; zeichnen Sie MN parallel zu OC, MN schneidet den gegebenen Kreis in N - der Bogen AN ergibt den siebzehnten Teil des ganzen Umfangs.”[2]
Construction description (english)
(Original text)
T. P. Stowell of Rochester, N. Y. writes:
"To construct a regular polygon of seventeen sides in a circle. Draw the radius CO at right-angles to the diameter AB: On OC and OB, take OQ equal to the half, and OD equal to the eighth part of the radius: Make DE and DF each equal to DQ and EG and FH respectively equal to EQ and FQ; take OK a mean proportional between OH and OQ,[1] and through K, draw KM parallel to AB, meeting the semicircle described on OG in M; draw MN parallel to OC, cutting the given circle in N - the arc AN is the seventeenth part of the whole circumference."[2]
Einzelnachweise / References
- ↑ a b Universität Magdeburg A.14 Mittelwerte. Mittlere Proportionale, Seite 2, Punkt u. Bild: b) (PDF-Datei) accessdate 30. April 2017
- ↑ a b Hendricks, J. E. (1877). "Answer to Mr. Heal's Query; T. P. Stowell of Rochester, N. Y.". The Analyst: A Monthly Journal of Pure And Applied Mathematicus Vol.1: 94–95. Query, by W. E. Heal, Wheeling, Indiana p. 64; abgerufen am 30. April 2017
Lizenz
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Kurzbeschreibungen
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
29. April 2017
image/gif
ce8de36ee608bc3353fac557e4a894b5939143fb
63.219 Byte
98,99999999999991 Sekunde
539 Pixel
744 Pixel
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 10:28, 10. Mai 2024 | 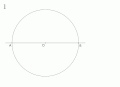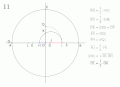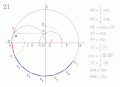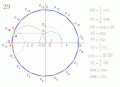 | 744 × 539 (62 KB) | wikimediacommons>Petrus3743 | Anzahl Konstruktionsschritte korr. |
Dateiverwendung
Die folgende Seite verwendet diese Datei:
