Interaktionsnetze

Interaktionsnetze sind ein graphisches Berechnungsmodell, das 1990 vom französischen Mathematiker Yves Lafont als Verallgemeinerung der Beweisstrukturen der linearen Logik entwickelt wurde.

Ein Interaktionsnetzsystem wird durch eine Menge von Agententypen und eine Menge von Interaktionsregeln spezifiziert. Interaktionsnetze sind ein inhärent verteiltes Berechnungsmodell, da Berechnungen gleichzeitig in vielen Teilen eines Interaktionsnetzes stattfinden können, ohne dass eine Synchronisation erforderlich ist. Letzteres wird durch die starke Konfluenz-Eigenschaft der Reduktion in diesem Berechnungsmodell garantiert. Dadurch bieten Interaktionsnetze eine natürliche Sprache für massive Parallelität. Sie bilden das Fundament vieler Implementierungen des Lambda-Kalküls, wie etwa effizienter geschlossener Reduktion und optimaler Reduktion im Sinne von Lévy, wie in Lambdascope.

Definitionen

Interaktionsnetze sind ungerichtete Graphen mit beschrifteten Knoten. Die Knoten werden auch Agenten genannt.

Ein Agent vom Typ α mit Stelligkeit $\text{ar}(\alpha )=n\ge 0$ besitzt einen Hauptport und $n$ Nebenports. Jeder Port kann mit höchstens einer Kante verbunden sein, und jede Kante verbindet genau zwei Ports. Nicht mit einer Kante verbundene Ports werden als freie Ports bezeichnet. Die Menge aller freien Ports bildet die Schnittstelle eines Interaktionsnetzes. Alle Agententypen gehören zu einer Menge $\mathrm{\Sigma }$, die als Signatur bezeichnet wird.

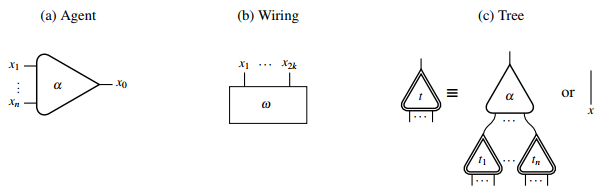
Ein Interaktionsnetz, das ausschließlich aus Kanten besteht, wird als Verdrahtung ("Wiring") bezeichnet und üblicherweise mit $\omega$ notiert. Ein Baum $t$ mit Wurzel $x$ wird induktiv entweder als einzelne Kante $x$ definiert oder als Agent α mit seinem freien Hauptport x sowie seinen Nebenports $x_i$, die mit den Wurzeln anderer Bäume $t_i$ verbunden sind.

Graphisch lassen sich die primitiven Strukturen von Interaktionsnetzen wie folgt darstellen:

Fehler beim Erstellen des Vorschaubildes:

Wenn zwei Agenten über ihre Hauptports miteinander verbunden sind, bilden sie ein aktives Paar. Für aktive Paare können Interaktionsregeln definiert werden, die beschreiben, wie das aktive Paar umgeschrieben wird. Ein Interaktionsnetz ohne aktive Paare befindet sich in Normalform. Eine Signatur $\mathrm{\Sigma }$ (mit einer darauf definierten Abbildung $\text{ar}:\mathrm{\Sigma }\to \mathbb{N}$) zusammen mit einer Menge von Interaktionsregeln für Agenten $\alpha \in \mathrm{\Sigma }$ bildet ein Interaktionssystem.

Interaktionskalkül

Die textuelle Repräsentation von Interaktionsnetzwerken wird als Interaktionskalkül bezeichnet und kann als Programmiersprache betrachtet werden.

Im Interaktionskalkül entsprechen induktiv definierte Bäume Termen der Form $t::=\alpha (t_1,\dots ,t_n)|x$, wobei $x$ als Name bezeichnet wird.

Jedes Interaktionsnetz $N$ kann unter Verwendung der zuvor definierten Verdrahtungs- und Baumprimitive wie folgt in ein äquivalentes Netz umgeschrieben werden:

Interaction Net as Configuration

Im Interaktionskalkül beschreibt eine Konfiguration eine "Momentaufnahme" eines Interaktionsnetzes.

Eine Konfiguration im Interaktionskalkül hat die Form:

$c\equiv ⟨t_1,\dots ,t_m|v_1=w_1,\dots ,v_n=w_n⟩$

und besteht aus zwei Teilen:

1. Schnittstelle (links vom Trennstrich): Eine geordnete Liste von Termen $t_1,...,t_m$, die die "externen Anschlüsse" des Netzes darstellen.
2. Gleichungen (rechts vom Trennstrich): Eine ungeordnete Multimenge von Gleichungen $v_1=w_1,\dots ,v_n=w_n$, die die internen Verbindungen des Netzes darstelle. Wie zuvor beschrieben, meint $\omega$ hierbei eine Verdrahtung. Wichtig ist, dass jeder Name in der Verdrahtung genau zweimal vorkommen muss.

Genau wie im Lambda-Kalkül sind im Interaktionskalkül die Konzepte der α-Konversion und der Substitution natürlich auf Konfigurationen definiert. Insbesondere können beide Vorkommen eines Namens durch einen neuen Namen ersetzt werden, sofern dieser nicht bereits in der gegebenen Konfiguration vorkommt. Konfigurationen werden bis auf α-Konversion als äquivalent betrachtet.

Die Substitution $t[x:=u]$ ist das Ergebnis des Ersetzens des Namens $x$ in einem Term $t$ durch einen anderen Term $u$, sofern $x$ genau einmal im Term $t$ vorkommt.

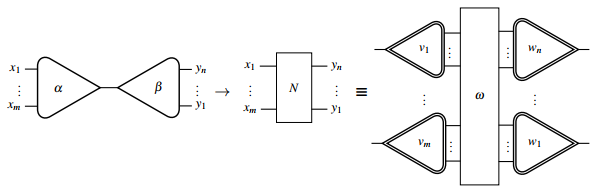
Jede Interaktionsregel kann wie folgt graphisch dargestellt werden:

Interaction Rule

Hier werden $\alpha ,\beta \in \mathrm{\Sigma }$, sowie das Interaktionsnetz $N$ in der Mitte, durch die Nutzung von Verdrahtungs- und Baumprimitiven in ein equivalentes Netz umgeschrieben, um sie mittels Lafonts Notation im Interaktionskalkül als $\alpha [v_1,\dots ,v_m]\bowtie \beta [w_1,\dots ,w_n]$ darzustellen.

Wenn $\alpha [v_1,\dots ,v_m]\bowtie \beta [w_1,\dots ,w_n]$, dann wird die Reduktion $⟨\overrightarrow{t}|\alpha (t_1,\dots ,t_m)=\beta (u_1,\dots ,u_n),\mathrm{\Delta }⟩\to ⟨\overrightarrow{t}|t_1=v_1,\dots ,t_m=v_m,u_1=w_1,\dots ,u_n=w_n,\mathrm{\Delta }⟩$ eine Interaktion genannt.

Hat eine der Gleichungen die Form $x=u$, so kann eine Indirektion angewandt werden:

$⟨\dots t\dots |x=u,\mathrm{\Delta }⟩\to ⟨\dots t[x:=u]\dots |\mathrm{\Delta }⟩$

oder

$⟨\overrightarrow{t}|x=u,t=w,\mathrm{\Delta }⟩\to ⟨\overrightarrow{t}|t[x:=u]=w,\mathrm{\Delta }⟩$.

Eine Gleichung der Form $x=t$ heißt Deadlock, wenn der Name $x$ in $t$ vorkommt. Grundsätzlich werden nur Deadlock-freie Interaktionsnetze betrachtet. Gemeinsam definieren Interaktion und Indirektion die Reduktionsrelation auf Konfigurationen. Die Tatsache, dass eine Konfiguration $c$ zu ihrer Normalform $c^{\prime }$ reduziert, wobei keine Gleichungen mehr übrig sind, wird als $c\downarrow c^{\prime }$ notiert.

Eigenschaften

Interaktionsnetze profitieren von den folgenden Eigenschaften, welche gemeinsam massive Parallelisierung ermöglichen:

• Lokalität: Nur aktive Paare können ersetzt werden.
• Linearität: Umformungsregeln können in konstanter Zeit angewendet werden.
• Starke Konfluenz: Wenn zwei Reduktionen $c\to c_1$und $c\to c_2$ existieren, dann gibt es mindestens eine Konfiguration $c^{\prime }$, sodass $c_1\to c^{\prime }$ und $c_2\to c^{\prime }$.

Interaktionskombinatoren

Eines der primitivsten Interaktionsysteme, welches immer noch mächtig genug ist, um alle anderen Interaktionsysteme zu simulieren, ist das System der Interaktionskombinatoren.

Die Signatur dieses Systems ist $\mathrm{\Sigma }=\{ϵ,\delta ,\gamma \}$, wobei $\text{ar}(ϵ)=0$ und $\text{ar}(\delta )=\text{ar}(\gamma )=2$.

Die Interaktionsregeln lauten:

• Löschung: $ϵ\bowtie \alpha [ϵ,\dots ,ϵ]$
• Duplikation: $\delta [\alpha (x_1,\dots ,x_n),\alpha (y_1,\dots ,y_n)]\bowtie \alpha [\delta (x_1,y_1),\dots ,\delta (x_n,y_n)]$
• Annihilation: $\delta [x,y]\bowtie \delta [x,y]$ sowie $\gamma [x,y]\bowtie \gamma [y,x]$

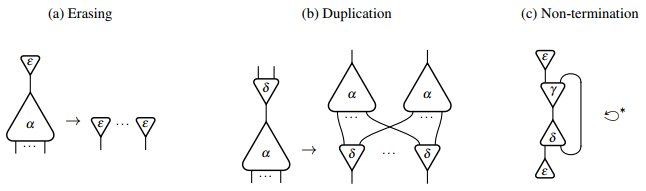
Die Anwendungen der Löschung und Duplikation sind in (a) und (b) in der folgenden Grafik dargestellt.

Fehler beim Erstellen des Vorschaubildes:

Rechts im Bild ist ein nicht-terminierendes Netz zu sehen, welches durch Anwendung der Interaktionsregeln nach drei Schritten wieder in die ursprüngliche Konfiguration reduziert wird, und somit nie eine Normalform erreichen kann. Diese endlose Sequenz an Reduktionen lautet im Interaktionskalkül folgendermaßen:

$\begin{array}{cc}& ⟨\varnothing |\delta (ϵ,x)=\gamma (x,ϵ)⟩\to \\ & ⟨\varnothing |ϵ=\gamma (x_1,x_2),x=\gamma (y_1,y_2),x=\delta (x_1,y_1),ϵ=\delta (x_2,y_2)⟩{\to }^{*}\\ & ⟨\varnothing |x_1=ϵ,x_2=ϵ,x=\gamma (y_1,y_2),x=\delta (x_1,y_1),x_2=ϵ,y_2=ϵ⟩{\to }^{*}\\ & ⟨\varnothing |\delta (ϵ,x)=\gamma (x,ϵ)⟩\to \dots \end{array}$

Nicht-deterministische Erweiterung

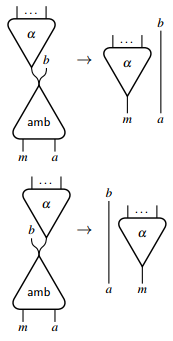
Interaktionsnetze sind im Wesentlichen deterministisch und können nicht direkt verwendet werden, um nicht-deterministische Berechnungen zu modellieren. Um nicht-deterministische Wahl auszudrücken, müssen Interaktionsnetze erweitert werden. Es reicht aus einen einzelnen Agenten, hier "amb" genannt, mit zwei Hauptports und den folgenden Interaktionsregeln einzuführen.

Non-deterministic Agent

Ein solcher Agent repräsentiert Wahl und kann verwendet werden, um jeden anderen Agenten mit einer beliebigen Anzahl von Hauptports zu simulieren. Zum Beispiel ermöglicht er die Definition einer "parallelen oder" ($ParallelOr$) Operation, die wahr zurückgibt, wenn mindestens eines ihrer Argumente wahr ist – unabhängig davon, welche Berechnung für die anderen Argumente ausgeführt wird.

Siehe auch

• Geometry of interaction
• Graphersetzungssystem
• Lambda-Kalkül
• Linear graph grammar
• Linear logic
• Proof net