Wärmeflusssensor

Eine Wärmeflussplatte, sie wird bei der Messung des Wärmewiderstandes von Wärme- und Wärmefluss auf Gebäudehüllen (Wände, Dächer) und in der Meteorologie verwendet. Der Sensor kann auch eingegraben werden, um den Bodenwärmefluss zu messen. Durchmesser 80 mm

Sensor für kombinierte Wärmefluss- und Temperaturmessung. Dieser Sensor wird hauptsächlich für Anwendungen in der Gebäudephysik verwendet.

Ein Wärmeflusssensor nutzt den physikalische Effekte um ein Messsignal proportional zum Wärmestrom oder der Wärmestromdichte durch seine Fläche zu generieren. Wärmeflusssensoren werden bei der Produktion kalibriert. Die Wärmestromdichte ergibt sich aus dem gemessenen Wärmestrom pro Fläche des Sensors. Alle Arten von Wärmeübertragung, wie Konvektion, Wärmeleitung und Strahlung werden gemessen.

Wärmeflusssensoren sind zum Beispiel das Gardon Meter, Dünnschichtthermosäulen, das Schmidt-Boelter Meter, und die Atomlagethermosäulen (Atomic Layer Thermopile =ALTP) Sensoren. Die SI-Einheit des Wärmestroms oder Wärmeflusses ist Watt, die der Wärmestromdichte ist Watt pro Quadratmeter.

Verschiedene Messmethoden wurden entwickelt und eine Kategorisierung nach physikalischem Messprinzip befindet sich in folgender Tabelle.

Nr.	Kategorie	Beschreibung
1	Analogie des Stofftransports	Messmethoden, die eine Analogie zwischen Stoff- und Wärmetransport ausnutzen, z. B. Naphthalin-Sublimations-Methode.
2	Methoden mit direkter Energiezu- und -abfuhr	Die Energiedissipation durch Heizung oder Kühlung eines angeströmten Körpers unter der Annahme eines quasistationärem Gleichgewichts zwischen Wärmezufuhr und -verlust liefert den direkten Zusammenhang zwischen Temperaturverlauf und Wärmestrom, z. B. mit einer CTA-Brücke (constant temperature anemometer) betriebene Oberflächenheißfilme.
3	Kalorimetrische Methoden	Aus dem zeitaufgelösten Oberflächentemperaturverlauf, z. B. gemessen durch Thermoelemente oder Dünnfilme, wird auf Basis eines analytischen Wärmeleitungsmodell (kalorimetrisches Modell mit bekannten Stoffwerten, Cook-Feldermann-Algorithmus) der Wandwärmefluss bestimmt.
4	Differenzielle Wärmeflussmethoden	Der Temperaturgradient in einem Material mit bekannten thermischen Eigenschaften wird mit Hilfe von Temperatursensoren auf der Ober- und Unterseite des Materials gemessen. Der Temperaturgradient mit den bekannten Stoffeigenschaften ist proportional zum Wandwärmestrom, z. B. Gardon, Schmidt-Boelter-, Mikro-(HFM)-Sensoren.
5	Methoden basierend auf dem Transversen Seebeck-Effekt (TSE)	Der Transverse Seebeck-Effekt eines thermisch anisotropen Materials liefert ein Messsignal, das einen linearen Zusammenhang mit dem Temperaturgradienten liefert. Der Proportionalitätsfaktor zwischen Temperaturgradient und Wandwärmefluss muss mit Hilfe einer Kalibriermethodik bestimmt werden, z. B. ALTP-Sensoren

Anwendung

Wärmeflusssensoren werden zum Beispiel zur Qualitätsanalyse von Gebäudeisolierungen oder zur Bestimmung thermischer Eigenschaften von Textilien mit Hilfe des Wärmedurchgangskoeffizienten eingesetzt. Andere Anwendungen sind Messungen von Strömungen in Flüssigkeiten, nicht invasive Körperkern-Temperaturmessung und das Messen der Leistung eines Laserstrahles.

Bauphysik

Große Mengen Energie sind zum Heizen und Kühlen von Gebäuden nötig. Daher kan es hilfreich sein, mit Hilfe eines Wärmeflusssensors die Qualität der Wärmedämmung von Gebäuden und den Wärmedurchgangskoeffizienten zu bestimmen.

Nach dem Gesetz der Wärmeübertragung ist der Wärmestrom durch eine Oberfläche, z. B. die einer Gebäudewand, proportional zur Differenz der inneren und äußeren Oberflächentemperatur des Objektes bzw. der Umgebungstemperatur. Dieser Proportionalitätsfaktor ist der Wärmedurchgangskoeffizient oder U-Wert. Je kleiner der U-Wert, desto besser ist die thermische Isolierung.

Textilien

Der Wärmefluss ist ein wichtiger Parameter bei der Entwicklung von Textilien mit speziellen thermischen Eigenschaften, wie zum Beispiel Sportbekleidung oder Brandschutzkleidung. Durch das Verwenden eines Wärmeflusssensors kann der thermische Durchgangskoeffizient bestimmt werden. Er stellt eine Verarbeitungs- und Materialeigenschaft dar.

Luft- und Raumfahrttechnik, Windkanäle, Triebwerke

Die Bestimmung von Wärmelasten ist die zentral für die Auslegung von Flugkörpern und Triebwerken. Deren Bestimmung erfolgt zum Beispiel in Windkanälen und Prüfstanden. Auf Grund der instationären Strömungsverhältnisse kommen Wärmeflusssensoren mit hoher zeitlicher Auflösung wie Dünnschicht Thermosäulen und ALTP-Wärmeflusssensoren zum Einsatz. Die ALTPs sind die schnellsten Wärmeflusssensoren und erreichen eine Zeitauflösung im Mikrosekundenbereich.

Eigenschaften

Ein Wärmeflusssensor misst die lokale Wärmestromdichte in eine Richtung. Das Resultat wird in [W/m²] angegeben. Die Berechnung erfolgt mit folgender Formel.

Funktionsprinzip eines Wärmeflusssensors

${\varphi }_q=\frac{V_{\mathrm{s}\mathrm{e}\mathrm{n}}}{E_{\mathrm{s}\mathrm{e}\mathrm{n}}}$

$V_{\mathrm{s}\mathrm{e}\mathrm{n}}$ ist das Ausgangssignal des Sensors (eine elektrische Spannung) und $E_{\mathrm{s}\mathrm{e}\mathrm{n}}$ ist die Kalibrationskonstante, diese ist sensorspezifisch.

Aufbau

Wärmeflusssensoren haben eine flache Plattenform und messen Wärmeströme senkrecht zur Sensorfläche.

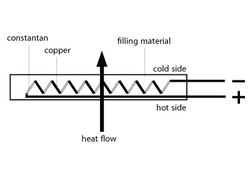
In den Wärmeflusssensoren sind Thermoelemente in Serie geschaltet (Thermosäule). Der Vorteil dieser Thermosäulen ist ihre Stabilität, ein geringer ohmscher Widerstand mit der Folge geringer elektromagnetischer Störanfälligkeit und einem guten Signal-Stör Verhältnis. Solche Sensoren erfordern keinen Nullpunktabgleich – sie liefern bei fehlendem Wärmestrom auch keine Ausgangsspannung.